假设检验
出自 MBA智库百科(https://wiki.mbalib.com/)
假设检验(Hypothesis Testing)
目录 |
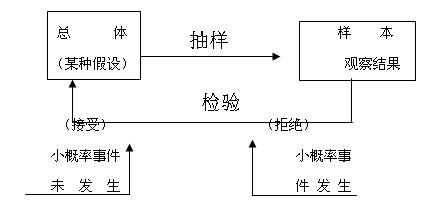
假设检验是用来判断样本与样本,样本与总体的差异是由抽样误差引起还是本质差别造成的统计推断方法。其基本原理是先对总体的特征作出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受作出推断。
生物现象的个体差异是客观存在,以致抽样误差不可避免,所以我们不能仅凭个别样本的值来下结论。当遇到两个或几个样本均数(或率)、样本均数(率)与已知总体均数(率)有大有小时,应当考虑到造成这种差别的原因有两种可能:一是这两个或几个样本均数(或率)来自同一总体,其差别仅仅由于抽样误差即偶然性所造成;二是这两个或几个样本均数(或率)来自不同的总体,即其差别不仅由抽样误差造成,而主要是由实验因素不同所引起的。假设检验的目的就在于排除抽样误差的影响,区分差别在统计上是否成立,并了解事件发生的概率。
在质量管理工作中经常遇到两者进行比较的情况,如采购原材料的验证,我们抽样所得到的数据在目标值两边波动,有时波动很大,这时你如何进行判定这些原料是否达到了我们规定的要求呢?再例如,你先后做了两批实验,得到两组数据,你想知道在这两试实验中合格率有无显著变化,那怎么做呢?这时你可以使用假设检验这种统计方法,来比较你的数据,它可以告诉你两者是否相等,同时也可以告诉你,在你做出这样的结论时,你所承担的风险。假设检验的思想是,先假设两者相等,即:μ=μ0,然后用统计的方法来计算验证你的假设是否正确。
1.小概率原理
如果对总体的某种假设是真实的,那么不利于或不能支持这一假设的事件A(小概率事件)在一次试验中几乎不可能发生的;要是在一次试验中A竟然发生了,就有理由怀疑该假设的真实性,拒绝这一假设。
2.假设的形式
H0——原假设, H1——备择假设
双尾检验:H0:μ = μ0 ,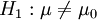
单尾检验: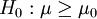 ,H1:μ < μ0
,H1:μ < μ0
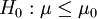 , H1:μ > μ0
假设检验就是根据样本观察结果对原假设(H0)进行检验,接受H0,就否定H1;拒绝H0,就接受H1。
, H1:μ > μ0
假设检验就是根据样本观察结果对原假设(H0)进行检验,接受H0,就否定H1;拒绝H0,就接受H1。
一般地说,对总体某项或某几项作出假设,然后根据样本对假设作出接受或拒绝的判断,这种方法称为假设检验。
假设检验使用了一种类似于“反证法”的推理方法,它的特点是:
(1)先假设总体某项假设成立,计算其会导致什么结果产生。若导致不合理现象产生,则拒绝原先的假设。若并不导致不合理的现象产生,则不能拒绝原先假设,从而接受原先假设。
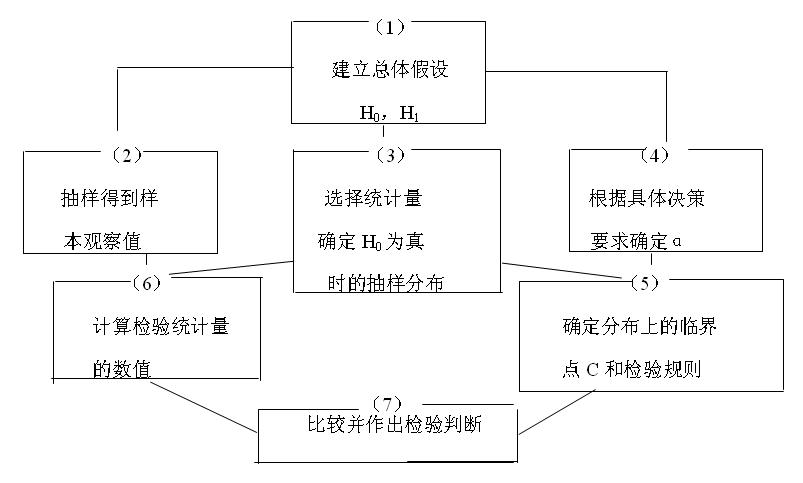
(2)它又不同于一般的反证法。所谓不合理现象产生,并非指形式逻辑上的绝对矛盾,而是基于小概率原理:概率很小的事件在一次试验中几乎是不可能发生的,若发生了,就是不合理的。至于怎样才算是“小概率”呢?通常可将概率不超过0.05的事件称为“小概率事件”,也可视具体情形而取0.1或0.01等。在假设检验中常记这个概率为α,称为显著性水平。而把原先设定的假设成为原假设,记作H0。把与H0相反的假设称为备择假设,它是原假设被拒绝时而应接受的假设,记作H1。
假设检验可分为正态分布检验、正态总体均值分布检验、非参数检验三类。
正态分布检验包括三类:JB检验、KS检验、Lilliefors检验,用于检验样本是否来自于一个正态分布总体。
正态总体均值检验检验分析方法和分析结果的准确度,考察系统误差对测试结果的影响。从统计意义上来说,各样本均值之差应在随机误差允许的范围之内。反之,如果不同样本的均值之差超过了允许的范围,这就说明除了随机误差之外,各均值之间还存在系统误差,使得各均值之间出现了显著性差异。
正态总体均值检验分为两种情况,
t检验是用小样本检验总体参数,特点是在均方差不知道的情况下,可以检验样本平均数的显著性,分为单侧检验与双侧检验。当为双样本检验时,在两样本t检验中要用到F检验。
从两研究总体中随机抽取样本,要对这两个样本进行比较的时候,首先要判断两总体方差是否相同,即方差齐性。若两总体方差相等,则直接用t检验,若不等,可采用t'检验或变量变换或秩和检验等方法。
Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。
上面所述的检验都是基于样本来自正态总体的假设,在实际工作中,有时并不明确知道样本是否来自正态总体,这就为假设检验带来难度。非参数检验方法,对样本是否来自正态总体不做严格的限制,而且计算简单。统计工具箱提供了符号检验和秩和检验两种非参数检验方法。
假设检验的基本思想是小概率反证法思想。小概率思想是指小概率事件(P<0.01或P<0.05)在一次试验中基本上不会发生。反证法思想是先提出假设(检验假设H0),再用适当的统计方法确定假设成立的可能性大小,如可能性小,则认为假设不成立,若可能性大,则还不能认为假设不成立。
- 1.确定检验规则
检验过程是比较样本观察结果与总体假设的差异。差异显著,超过了临界点,拒绝H0;反之,差异不显著,接受H0。
差异 临界点 判断 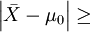
c 拒绝H0 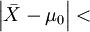
c 接受H0
怎样确定c?
- 2.两类错误
接受或拒绝H0,都可能犯错误
I类错误——弃真错误,发生的概率为α
II类错误——取伪错误,发生的概率为β
检验决策 H0为真 H0非真 拒绝H0 犯I类错误(α) 正确 接受H0 正确 犯II类错误(β)
α大β就小,α小β就大
基本原则:力求在控制α前提下减少β
α——显著性水平,取值:0.1, 0.05, 0.001, 等。如果犯I类错误损失更大,为减少损失,α值取小;如果犯II类错误损失更大,α值取大。
确定α,就确定了临界点c。
①设有总体:X~N(μ,σ2),σ2已知。
②随机抽样:样本均值\bar{X}~N(\mu,\sigma^2/n)。
③ 标准化:
标准化: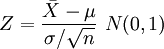
④确定α值,
⑤查概率表,知临界值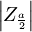
⑥计算Z值,作出判断。
1、做假设检验之前,应注意资料本身是否有可比性。
2、当差别有统计学意义时应注意这样的差别在实际应用中有无意义。
3、根据资料类型和特点选用正确的假设检验方法。
4、根据专业及经验确定是选用单侧检验还是双侧检验。
5、当检验结果为拒绝无效假设时,应注意有发生I类错误的可能性,即错误地拒绝了本身成立的H0,发生这种错误的可能性预先是知道的,即检验水准那么大;当检验结果为不拒绝无效假设时,应注意有发生II类错误的可能性,即仍有可能错误地接受了本身就不成立的H0,发生这种错误的可能性预先是不知道的,但与样本含量和I类错误的大小有关系。
6、判断结论时不能绝对化,应注意无论接受或拒绝检验假设,都有判断错误的可能性。
7、报告结论时是应注意说明所用的统计量,检验的单双侧及P值的确切范围。
假设检验与置信区间有密切的联系,我们往往可以由某参数的显著性水平为α的检验,得到该参数的置信度为1—α的置信区间,反之亦然。例如,显著性水平α的均值μ的双侧检验问题:
H0:μ = μ0, 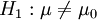
与置信度为1-α 的置信区间之间有着这样的关系;若检验在α水平下接受H0,则μ的1 - α的置信区间必须包含μ0;反之,若检验在 α水平下拒绝H0,则μ的1-α的置信区间必定不包含μ0。因此,我们可以用构造μ的1-α置信区间的方法来检验上述假设,如果构造出来的置信区间包含μ0,就接受H0;如果不包含μ0就拒绝H0。同样给定显著水平 α,可以从构造检验规则的过程中,得到μ的 1-α置信区间。 如上例,μ的置信度为95%的置信区间为:
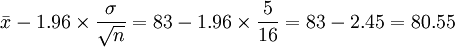
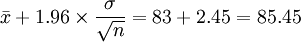
即置信区间为(80.55 , 85.45),因为μ0 = 80,不在这个区间内,拒绝H0
考虑下面三种类型的假设检验: (4.12)
(1)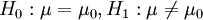 (双边检验)
(双边检验)
(2)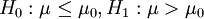 (右侧单边检验)
(右侧单边检验)
(3)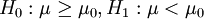 (左侧单边检验)
(左侧单边检验)
案例一:假设检验设备判断中的应用[1]
例如:某公司想从国外引进一种自动加工装置。这种装置的工作温度X服从正态分布(μ,52),厂方说它的平均工作温度是80度。从该装置试运转中随机测试16次,得到的平均工作温度是83度。该公司考虑,样本结果与厂方所说的是否有显著差异?厂方的说法是否可以接受?
类似这种根据样本观测值来判断一个有关总体的假设是否成立的问题,就是假设检验的问题。我们把任一关于单体分布的假设,统称为统计假设,简称假设。上例中,可以提出两个假设:一个称为原假设或零假设,记为H0:μ=80(度);另一个称为备择假设或对立假设,记为H1 :μ≠80(度)这样,上述假设检验问题可以表示为:
H0:μ=80 H1:μ≠80
原假设与备择假设相互对立,两者有且只有一个正确,备择假设的含义是,一旦否定原假设H0,备择假设H1备你选择。所谓假设检验问题就是要判断原假设H0是否正确,决定接受还是拒绝原假设,若拒绝原假设,就接受备择假设。
应该如何作出判断呢?如果样本测定的结果是100度甚至更高(或很低),我们从直观上能感到原假设可疑而否定它,因为原假设是真实时,在一次试验中出现了与80度相距甚远的小概率事件几乎是不可能的,而现在竟然出现了,当然要拒绝原假设H0。现在的问题是样本平均工作温度为83度,结果虽然与厂方说的80度有差异,但样本具有随机性,80度与83度之间的差异很可能是样本的随机性造成的。在这种情况下,要对原假设作出接受还是拒绝的抉择,就必须根据研究的问题和决策条件,对样本值与原假设的差异进行分析。若有充分理由认为这种差异并非是由偶然的随机因素造成的,也即认为差异是显著的,才能拒绝原假设,否则就不能拒绝原假设。假设检验实质上是对原假设是否正确进行检验,因此,检验过程中要使原假设得到维护,使之不轻易被否定,否定原假设必须有充分的理由;同时,当原假设被接受时,也只能认为否定它的根据不充分,而不是认为它绝对正确。
案例二:假设检验在卷烟质量判断中的应用[2]
在卷烟生产企业经常会遇到如下的问题:卷烟检验标准中要求烟支的某项缺陷的不合格品率P不能超过3%,现从一批产品中随机抽取50支卷烟进行检验,发现有2支不合格品,问此批产品能否放行?按照一般的习惯性思维:50支中有2支不合格品,不合格品率就是4%,超过了原来设置的3%的不合格品率,因此不能放行。但如果根据假设检验的理论,在α=0.05的显著性水平下,该批产品应该可以放行。这是为什么呢?
最关键的是由于我们是在一批产品中进行抽样检验,用抽样样本的质量水平来判别整批的质量水平,这里就有一个抽样风险的问题。举例来说,我们的这批产品共有10000支卷烟,里面有4支不合格品,不合格品率是0.04%,远低于3%的合格放行不合格品率。但我们的检验要求是随机抽样50支,用这50支的质量水平来判别整批 10000支的质量水平。如果在50支中恰好抽到了2支甚至更多的不合格品,简单地用抽到的不合格品数除以50来作为不合格品率来判断,那我们就会对这批质量水平合格的产品进行误判。
如何科学地进行判断呢?这就要用到假设检验的理论。
步骤1:建立假设
要检验的假设是不合格品率P是否不超过3%,因此立假设
H0:P≤0.03
这是原假设,其意是:与检验标准一致。
H1:P>0.03
步骤2:选择检验统计量,给出拒绝域的形式
若把比例P看作n=1的二项分别b(1,p)中成功的概率,则可在大样本场合(一般n≥25)获得参数p的近似μ的检验,可得样本统计量: 近似服从N(0,1)
其中=2/50=0.04,p=0.03,n=50
步骤3:给出显著性水平α,常取α=0.05。
步骤4:定出临界值,写出拒绝域W。
根据α=0.05及备择假设知道拒绝域W为
步骤5:由样本观测值,求得样本统计量,并判断。
结论:在α=0.05时,样本观测值未落在拒绝域,所以不能拒绝原假设,应允许这批产品出厂。
假设检验中的两类错误。
进一步研究一下这个例子,在50个样品中抽到多少个不合格品,就要拒绝入库呢?我们仍取α=0.05,根据上述公式,得出,解得x>3.48,也就是在50个样品中抽到4个不合格品才能判整批为不合格。
而如果我们改变α的取值,也就是我们定义的小概率的取值,比如说取α=0.01,认为概率不超过0.01的事件发生了就是不合理的了,那又会怎样呢?还是用上面的公式计算,则得出,解得x>4.30,也就是在50个样品中抽到5个不合格品才能判整批为不合格。检验要求是不合格品率P不能超过3%,而现在根据α=0.01,算出来50个样品中抽到5个不合格品才能判整批为不合格,会不会犯错误啊!假设检验是根据样本的情况作的统计推断,是推断就会犯错误,我们的任务是控制犯错误的概率。在假设检验中,错误有两类:
第一类错误(拒真错误):原假设H0为真(批产品质量是合格的),但由于抽样的随机性(抽到过多的不合格品),样本落在拒绝域W内,从而导致拒绝H0(根据样本的情况把批质量判断为不合格)。其发生的概率记为α,也就是显著性水平。α控制的其实是生产方的风险,控制的是生产方所承担的批质量合格而不被接受的风险。
第二类错误(取伪错误):原假设H0不真(批产品质量是不合格的),但由于抽样的随机性(抽到过少的不合格品),样本落在W外,从而导致接受H0(根据样本的情况把批质量判断为合格)。其发生的概率记为β。β控制的其实是使用方的风险,控制的是使用方所承担的接受质量不合格批的风险。
再回到刚刚计算的上例的情况,α由0.05变化为0.01,我们对批质量不合格的判断由50 个样本中出现4个不合格变化为5个,批质量是合格的而不被接受的风险就小了,犯第一类错误的风险小了,也就是生产方的风险小了;但同时随着α的减小对批质量不合格的判断条件其实放宽了——50个样本中出现4个不合格变化为5个,批质量是不合格的而被接受的风险大了;犯第二类错误的风险大了,也就是使用方的风险大了。 在相同样本量下,要使α小,必导致β大;要使β小,必导致α大,要同时兼顾生产方和使用方的风险是不可能的。要使α、β皆小,只有增大样本量,这又增加了质量成本。
因此综上所述,假设检验可以告诉我们如何科学地进行质量合格判定,又告诉我们要兼顾生产方和使用方的质量风险,同时考虑质量和成本的问题。
- ↑ 俞良蒂.统计学原理.第四章 参数估值与假设检验.中国地质大学(武汉)
- ↑ 孙厉.假设检验在卷烟质量判断中的应用
评论(共24条)
请问,大样本和小样本的界限是25还是30呀?还是不同的书有不同的规矩??大样本和小样本的假设检验会一样吗?
一切随缘。
请问,大样本和小样本的界限是25还是30呀?还是不同的书有不同的规矩??大样本和小样本的假设检验会一样吗?
30
请问,假设检验与置信区间的关系 μ的置信度为95%的置信区间为:
中1.96的是怎么来的 拜托拜托,上帝保佑你
查表
thx终于明白到底怎么设定原假设了:1、问:是否明显A事件,原假设就定为非A事件,充分否定了非A,才能保证明显A。2、问:是否A事件,原假设就定为A事件,不能充分否定A事件就说明A事件可能会发生。因为是基于小概率事件的反证,这两个解里面,如果α<0.5,问题1中A事件的变量取值域要小于问题2中A事件的变量的取值域,而差的这部分域刚好是变量以1-2α为置信水平的置信区间。而当α为0.5时,可以发现,这两个部分不会有差别了,那就可以换个思路了:不会存在明显和可能的差别了,某事件发生一次就说明了它发生了(因为发生与不发生是等概率的,不存在小概率这一称呼了)。当α>0.5时,显然这里的变量已经本来该小概率的事件变成了正常的,而正常的变成了小概率事件了,反过来理解就行了,不过这样α也失去了意义,毕竟其取值一般在0.05,0.025,0.01等。 回过来看,问题1可能发生变量的弃真,问题2可能会发生取伪(这也刚好说明了为什么问题1的变量取值域要小于问题2的变量取值域,弃的真和取的伪都集中在置信区间内)所以如果A事件为烟卷可以放行,1问题也就是明显可以放行,2问题也就是可以放行,这样就能和文中的对接上了。
thx终于明白到底怎么设定原假设了:1、问:是否明显A事件,原假设就定为非A事件,充分否定了非A,才能保证明显A。2、问:是否A事件,原假设就定为A事件,不能充分否定A事件就说明A事件可能会发生。因为是基于小概率事件的反证,这两个解里面,如果α<0.5,问题1中A事件的变量取值域要小于问题2中A事件的变量的取值域,而差的这部分域刚好是变量以1-2α为置信水平的置信区间。而当α为0.5时,可以发现,这两个部分不会有差别了,那就可以换个思路了:不会存在明显和可能的差别了,某事件发生一次就说明了它发生了(因为发生与不发生是等概率的,不存在小概率这一称呼了)。当α>0.5时,显然这里的变量已经本来该小概率的事件变成了正常的,而正常的变成了小概率事件了,反过来理解就行了,不过这样α也失去了意义,毕竟其取值一般在0.05,0.025,0.01等。 回过来看,问题1可能发生变量的弃真,问题2可能会发生取伪(这也刚好说明了为什么问题1的变量取值域要小于问题2的变量取值域,弃的真和取的伪都集中在置信区间内)所以如果A事件为烟卷可以放行,1问题也就是明显可以放行,2问题也就是可以放行,这样就能和文中的对接上了。
说的好!!!









very good!