黄金比率

出自 MBA智库百科(https://wiki.mbalib.com/)

黄金比率(Golden Ratio)

　　黄金比率是指一连串神奇数字的组合，是技术分析中纯以数字运算的一种分析工具。

　　黄金比率是源于神奇数字（Fibonnacci Number Sequence）。黄金比率是由十三世纪末出生的意大利著名数学家Leonardo Fibonacci发现的，比率由一组神奇数字计算而成。这串神奇数列，是任何相列的两个数字之和都等于后一个数字。即：1，1，2，3，5，8，13，21，34，55，89，144……如此类推。即1＋1＝2，1＋2＝3，2＋3＝5，3＋5＝8等。

　　常用到的黄金数字，是0，0.236，0.382，0.5，0.618，0.764及1，此外，亦会用到1.382，1.618等数值，其实就是1以至2等整数加上黄金数字。

　　这些黄金数字，亦是出自这串神奇数列，如果以低一个数值除以高个数值，得出来的结果均会与0.618相近，亦是所取数字愈大，愈接近0.618。如2/3＝0.6667，8/13＝0.6154，89/144＝0.6181。

　　如果以低两个数值除以高个数值，得出来的结果均会与0.382相近，亦是所取数字愈大，愈接近0.382。如2/5＝0.4，8/21＝0.3810，55/144＝0.3819。

　　如果以低三个数值除以高个数值，得出来的结果均会与0.236相近，亦是所取数字愈大，愈接近0.216。如2/8＝0.25，8/34＝0.2353，34/144＝0.2361。

　　以一个数字除以前一个数位的比率，得出来的结果均会与1.618相近，所取数字愈大，愈接近1.618。如3/2＝1.5，21/13＝1.6154，144/89＝1.6180。

　　以一个数字除以前两个数位的比率，得出来的结果均会与2.618相近，所取数字愈大，愈接近2.618。如5/2＝2.5，34/13＝2.6154，144/55＝2.6182。

　　黄金数字间亦互有关系，如两个重要的黄金数字0.618及0.382，两者相加为1，即1－0.618＝0.382，所以可以利用同理将1－0.236＝0.764而将另一个黄金数字找出来，亦可将0.382乘2得出0.764。此外，将0.618除以0.382亦可得出另一个黄金数字1.618，将1.618除以0.618得出2.618。

　　严格来说，0.5并不是黄金数字，但由于在实际上经常遇到，所以亦并入黄金数字系列。由于这些黄金数字全数可由数列之数字相除得出，故亦称之为黄金比率。

　　透过这些比率，可以用来测试未来市况的上升目标或下跌目标，预测升市中的调整幅度，以及跌市中的反弹幅度等。黄金比率包括最常见的0.236倍比率、0.382倍比率、0.5倍比率、O.618倍比率、0.764倍比率、1.382倍比率、1.618倍比率、2倍及2.618倍比率等。由于黄金比率测市功效显著，准确性奇高，所以，得到市场人士广泛使用。

　　—般来说，在调整市中，黄金比率0.382倍、O.5倍及0.618倍被视为调整时之三级支持，支持力随向下调整的深度而逐级递增，即币况由高位回吐至0.382倍水平已有初步支持。若该位失守，市况将进一步下试0.5倍水平，此时支持力将明显较0.382倍之支持力为大。失去守0.5倍则要到0.618倍水平才有支持，而该位的支持力将较前两级之支持更大。市况若企稳该水平以上，后市基调仍然向好。

　　此外，另两个比率O.236倍及0.764倍则较为少用，其中前者主要在大型上升；目的中段出现，期间市况只作短暂回吐即获支持再上。而0.764倍比率则相对重要得多，主要是该比率对中期走势有重要指标作用。技术上，市况在中期升浪中只要调整不低于0.764倍，反复向上格局不变，否则升势将被打回原形，跌回升浪之起步点。而吕有出现转势的危机，目口原有升势可能结束，或转为一上落市。

　　至于反弹市方面，与调整市刚好相反，0.382倍、o.5倍及0.618倍比率被视为反弹时之三级阻力，阻力随向上反弹幅度而逐级递增，即股价由低位反弹上O.382倍附近已有初步阻力。

　　通常在突破0.382倍阻力后可望上试0.5倍水平，但该水平的阻力亦逐渐加大。若再向上突破，股价将进一步上试0.618倍强大阻力。后市若无法向上突破，走势仍是反复向下。

　　量度上升或下跌水平是黄金比率中一个最重要部分，原因是这些比率可以粗略评佰或测试市况向上或向下突破后的上升或下跌目标，上升阻力及下跌支持等。最常见的比率包括1.382倍、1．.618倍，2倍及2.618倍，即是说，当市况向上或向下突破后，市况将会朝着第一个上升或下跌目标1.382倍水平推进，若能进一步突破该水平，市况将再试1.618倍第二个目标……如此类推。而上升或下跌的阻力或支持将逐级增加。

　　黄金比率测市连确性相当高，无论在测试上升水平或下跌水平，调整市或反弹市幅度，偏差幅度相当有限。因此，对预测后市走势有非常高的参考价值。

　　1.斐波那奇序数可用于波浪宽度(时间)预测。在某一固定的时期内，依据艾略特波浪理论并不能预测时间因素，因此也就无法利用时间因素来预测市场的动态演变。但是，与斐波那奇序数相关联的时间关系又常常出乎意料地精确地反映了浪的宽度。在波浪分析中，时间周期表明可能发生转折的时间，尤其将目标价格和数浪相结合，能获得更好的效果。

　　在艾略特波浪理论中，一再强调“自然法则”，从波浪的数日可以发现与“斐波那奇序数”相当吻合。每一个波动周期都是以8浪完成，其中5浪上升，3浪下跌；较大波动周期有89浪；更大的级数有144浪，均为序列数字。

　　2.黄金比率可用于波段幅度的计算。在波浪理论中，每一个波浪之间的比例，包括波动幅度与时间长度的比较，均符合黄金比率n对于技术分析者来说，这是一个相当重要的参考依据。

　　黄金比率的分析，通常有下列关系：

　　(1)第3浪波动的幅度，为第1浪起涨点至第1浪最高点间隔度的某黄金比率数字，包括0.382、0.500、0.618、1.00O与1.618等。

　　(2)第2浪的调整幅度，约为第1浪涨幅的0.382、0.500、与0.618倍的幅度。

　　(3)在调整浪中，C浪与a浪之间的比例，也与黄金比率数字相吻合。通常C浪长度为a浪1.618倍，尤其在延伸型的平坦调整浪中更是如此。在某些状况下，C浪的底部低点经常低于a点之下，为a浪长度的0.618倍。

　　(4)第1浪至第5浪的完整波浪幅度，其极限约为第1浪涨幅的3.236倍。

　　(5)在倾斜三角形中的震荡走势中，每一浪长度为前…浪的0.618倍。

　　(6)第5浪的涨幅，也有可能为第1浪至第3浪全部涨幅的1.618倍。

　　1.当价位脱离底部开始上涨时，以底位价值为基数，其涨幅在接近某一黄金比率时，比较容易遇到阻力；当价怔脱离顶部下跌时，则以峰位价位为基数，跃幅在达到某一黄金比率时较有可能遇到支撑。

　　例如，电真空在1992年11月中旬结束下跌行情时的最低收盘价为11月10日的4.53元。反转上升后，投资者可计算出电真空各种不同的反压价位：4.53×1.191=5.40元，4.53×1.382=6.26元，4.53×1.5=6.80元，4.53×1.618=7.33元，4.53×1.809=8.19元，……，然后，再依照实际股价的变动作出买卖决策。当股价每次顺利通过一反压点时，则看下一个反压点，若疲软勉强则抛出股票。电真空的第一波行情实际上升到l四巴年12月3日的12.70元才回档，而根据黄金比率可计算出4.53x2.删＝12.73元，两者非常贴近。

　　又如，上证综合指数于1993年2月15日创下高价1536.82点点后转入弱势市场，首次在124.呢点得到支撑反弹，而在3月25日于945.42点遇强支撑，最后于3月31日见底925.91点反转。如以1536.82点为基数，则可以计算出如下文撑点：1536.82×0.809=1243.29点，1536.82×0.618=949.75点，与实际情况相比，误差也较小。

　　2.行情发生转势时，无论是止跌转升的反转抑或是止升转跌的反转，以近朔走势中重要的峰位和底位之间的涨跌差额作为汁其的基数，将原来的涨跌按0.191、0.382、0.5、0.618、0.肥分割为黄金点，价位在反转后的走势将有可能在这些黄金点上遇到阻力或文撑。

　　例如，在1992年12月上旬上证综合指数于808.20点遇阻回档，在625.23点迢支撑止跌(最低探底至枷点以下)，跌幅为182.97点；如以393.52点至808.20点的涨幅414.68点为基数，按黄金比率0.5可以算出从808.20点回档的黄金支撑位为808.20-414.68=393.52点，与实际相比，误差为24.37点。

　　需要指出的是，由于个股容易被机构和大户操纵，因此应用黄金比率可能会出现一定的误差。但是，机构和大户对整个股市则难于操纵，因此，黄金比率更适用于预测整个股市的大势。

一、黄金比率在服装效果图中的运用

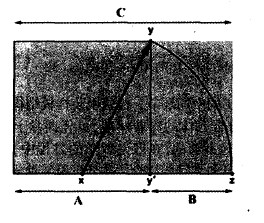
　　服装效果图的主要功能是：1.体现服装款式和穿着效果；2.传达设计者思想意识和设计风格；3.呈现绘画艺术的视觉美。可以通俗地讲，服装效果图既是生产用的工业图纸。又是具有极强美感的绘画作品。因此，它在“构图”形式、内容表达、画面效果处理等方面都不可忽视．其中服装效果图的“构图”极为重要，它能准确地表现作品的主题思想和美感效果。在进行效果图的模特儿、道具等的布局、设计时，首先要确立画面的“趣味中心”.原因是它最容易抓到“眼球”的吸引力。其次找出所绘图纸的“黄金比率线”，应该把主要的模特儿放“黄金比率线”的位置，“黄金比率线”最能突出画面的“趣味中心”。最后把其它的人、物放到相应的地方，即完成了以个别或局部的形象组成的艺术整体的服装效果图的构图。“黄金比率线”如下图找出：“黄金分割”公式用图形来解释更直观。先画一正方形并将底边分成二等分，再取中点x，以x为圆心，再以XY线段为半径画圆，它与底边直线的交点是z点。这样原来的正方形就延伸为一个以5：8为比率的矩形，(Y’点就是“黄金分割点”，YY’连线即称“黄金比率线”)，A：C=B：A=5：8。黄金比率具有严格的比例性、审美的艺术性、实用的和谐性，并蕴藏着丰富的美学价值。

　　二、黄金比率在服装款式设计中的运用

　　服装的款式设计包括：整体廓型设计、局部样式设计两大方面。尽管整体廓型设计是指服装的外型轮廓，即A型、H型、s型、V型、O型等，但是每个廓型都有宽度和长度的配比关系。对于宽松型的V型、O型等的服装，宽度和长度的比例可以采用黄金比率或比例随意定制。可是对于紧身型或合体型的服装，在宽度和长度的比例设置上有严格的要求，如紧身型(即s型)的旗袍：旗袍的长度规格要以旗袍的肩宽、胸围、臀围等的规格为基础进行设计，采用黄金比率能更好地体现旗袍的清新典雅和雍容华贵。再如合体型(即H型)的西服或休闲装：西服或休闲装的长度均要以西服或休闲装的肩宽、胸围、臀围等的规格为基础进行设计．采用黄金比率能更好地体现西服的优雅、端庄，体现女性的柔美之韵以及男性的绅士风度。

　　服装的局部样式设计就是指服装的款式设计．款式设计是由形式美的法则来决定的。服装的形式美即是指服装的款式美，形式美的法则主要包括：比例、平衡、呼应、节奏、主次、统一。比例列在形式美的法则的首位可见它的重要性。比例可以表现为：上装与下装的比例、上装的局部与整体的比例、下装(尤指裙装)的局部与整体的比例等的比值。实践证明，近似于2／3，3／5，5／8，8／13…的黄金分割比率用于上装与下装的比例；用于上装的局部与整体的比例；用于下装(尤指裙装)的局部与整体的比例是最美的比例，也是设计家所公认的。

　　三、黄金比率在服装色彩搭配中的运用

　　黄金比率在服装色彩搭配中的运用，主要体现在服装的面料色彩、服装的上下和里外颜色的层次搭配等方面。服装面料的色彩，一般有单一色、两种或多种的套色、高科技混纺的感光色等等，除了单一的纯色外．几乎每种面料都涉及套色色彩的比例配置问题，要掌握每种颜色的面积大小，黄金比率能在此极大地发挥它的功效。

　　在服装的上下和里外颜色的层次搭配上，黄金比率同样能在此发挥它的重要作用。服装的上装和下装颜色的搭配可以用315或5／8的黄金比率，来达到视觉的平衡并产生美感。服装的外套和里装(或内衣等)颜色的搭配也可以用2／3，3／5或5／8的黄金比率，来加强色彩面积的对比效应，从而达到预期的形式美的效果。

　　服装的专业教学主要分三大块：服装款式设计、服装结构设计、服装工艺设计。以上三方面主要谈的是黄金比率在服装款式设计教学的运用。其实，黄金比率在服装结构设计、服装工艺设计中的运用也很广泛。譬如，服装结构设计中衣长与胸围的规格设定；分割线位置的设定；省道、褶裥的设定等都可参照黄金比率来产生形式美感。再如，服装工艺设计中前后衣片、衣领、门襟、口袋等整体与局部的工艺和装饰手法，在数量、面积等的比例关系均能运用黄金比率来达到满意的效果。

　　黄金比率不仅大量运用在工业品、日用品和工艺美术的设计中．而且在实际生活中应用得也非常广泛，例如：建筑物中的许多线段、主持人站在舞台长度的黄金分割点的位置、植物界嫩枝上的叶子排列等等。另外，在进行科学实验时，常常也使用黄金比率，用黄金比率合理地选择试验的次数(又称优选法)，不仅提高了工作的效率，而且达到事半功倍的效果。正因为黄金比率在各方面的广泛而重要的应用，所以人们一直珍称它为“黄金比率”