随机规划与随机控制ALM模型

出自 MBA智库百科(https://wiki.mbalib.com/)

随机规划与随机控制ALM模型（Stochastic Programming or Stochastic Control ALM Model）

　　目前的ALM模型越来越多地运用到随机规划或随机控制的方法。

　　（一）随机规划模型主要是通过运用事件树、生成场景等元素，来为金融机构的资金配置提供一个描述未来资产价格、收益和风险等不确定因素在某种概率条件下的变动趋势的分析框架。金融机构在处理资金配置中会面临复杂的限制条件，由于随机规划模型和方法接纳了一些更接近于现实的假设，并提供了一种动态方法来解决多期资金配置中的问题，因此它可以在一个框架中同时处理交易成本、多元状态变量、市场不完全性、税收和交易限制、监管限制、公司政策要求等多因素问题，从而为金融机构大批量地处理和分析多种不确定因素的影响提供了可能性。

　　国外金融学者对多期随机规划模型在金融机构的实际运用进行了大量的研究，并取得了许多成果。例如，布拉德里（Bradley）和克朗斯（Crane）于1973年，库斯（Kusy）和茨姆巴（Ziemba）于1986年为银行的ALM设计出了随机线性规划模型；马尔维（Mulvey）和瓦拉迪米罗（Vladimirou）于1992年为金融机构的资产配置提出了一个多期随机网络模型；卡里罗等（Carino et al.）于1994年为一家日本保险公司的资产负债管理问题构造了一个多期随机线性模型；希勒（Hiller）和厄可斯腾（Eckstein 1993），泽尼尔斯（Zenios 1993），古拉伯等（Golub et al 1993）则在20世纪90年代中期分别为固定收益证券管理构建了不同的随机规划模型。

　　其中公认比较有代表性的应该当属库斯（Kusy）和茨姆巴（Ziemba）于1986年为温哥华储蓄信贷协会的5年资金规划期设计出的一个简单补偿的多期随机线性规划模型，极大地推动了商业银行ALM理论的研究。在库斯-茨姆巴模型之后，ALM理论的另一里程碑式的贡献是卡里罗（Carino et al）等创建的Russell-Yasuda Kasai模型。Russell-Yasuda Kasai模型在日本Yasuda保险公司（Yasuda公司）进行尝试性运用，使该公司在满足账面价值规则及条例管制的同时，能遵循公司的经济价值，而且，该模型还可以对与公司业务环境相关联的事件结果来进行资产配置和负债管理决策，消除未来资产负债价值的不确定性。在使用这一模型的两年内，即1991年和1992年，按这一模型设计的投资策略，使Yasuda公司获得了7900万美元的额外收益。

　　（二）随机控制方法以状态的连续统（continuum）表示不确定状态，连续统的特征以少量服从联合马尔可夫过程的状态向量描述 。Brennan et al.分析了可以在债券、股票和现金方面投资的投资组合问题，假定有三个状态变量影响期望资产回报的时间变化，这三个变量即短期利率(r)、长期债券利息率(l)及股票资产组合分红收益(δ)。该文假定投资者没有负债，假定负债的期望增长率依赖于状态变量的水平，将负债包括进去相对来说很简单直接。如前所述，状态向量服从联合马尔可夫过程，该过程假设为以下形式：

　　dr = μ_rdt + σ_rdz_r

　　dl = μ_ldt + σ_ldz_l

　　dδ − μ_δdt + σ_δdz_δ

　　股票与债券由下式给定：

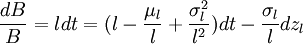
　　其中dS/S为股票组合的回报率，dB/B为债券的瞬时总回报。参数μ_iσ_i(i = r,l,δ,S)为状态变量r,l,δ的at most函数(at most function)，dz_i为维纳（Wiener）过程的增量。维纳过程增量间的相关系数为ρ_rl等。

　　定义W为财富，其效用假定为等弹性形式，即对于τ时r<的情况下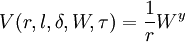，；定义x为组合中股票的比例，y为康索尔债券的比例，Bellman方程为：

　　max_x,yE[dV] = 0

　　解其一阶条件，可以找到最优控制解x ^* (r,l,δ,τ)和y ^* (r,l,δ,τ)，该过程可以由经验数据估计，投资者的最优控制问题可以通过参数值的估计得到解决。

　　Brennan和Schwartz^[1]通过允许投资者在短期利率期货如股票、债券或现金上采取长线或短线的情况扩展了这个模型，通过分析，他们认为这样的投资机会可以显著改善期望效用。其他一些研究人员利用这个理论讨论了大学捐赠基金的优化投资策略问题等^[2]。

　　随机规划ALM模型实际上是一类模型，它提供了模拟一般目标的方法。这些目标可以包括交易费用、税费、法律政策限制等方面的要求。由于考虑了众多因素，模型的变量越来越多，从而导致大量的优化问题，其计算成本相当高，因而实用性令人怀疑。我们以“机会限制模型（Chance Constrained Model）”为例。

　　机会限制模型最早由Charnes和Kirby提出 。在他们的论文里，将未来的存款与贷款支出看作是联合分布的随机变量，以资本充足率公式作为机会限制。该模型的缺点是，违背约束的情况并没有根据其数量给予惩罚。Charnes等将该方法应用于资产负债表的管理，另外两篇文章用该模型对保险公司的资产组合进行分析。

　　Dert在指定收益年金领域将该模型发展为多阶段机会限制模型（Multistage chance-constrained ALM model），与Charnes和Kirby不同的是，该作者以场景模拟不确定性而不是作分布假设。以该模型为例，该这个模型的目标函数是，在失去偿付能力的风险水平可以接受、确保及时支付指定收益的能力的稳定性的限制下实现筹资成本最小。其中偿付能力要求为基金剩余负债与相应偿付能力比率的乘积，资产价值低于要求的水平通过场景设定模拟。