重心法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

重心法(The centre-of-gravity method)

什么叫重心法?

　　重心法(The centre-of-gravity method)是一种设置单个厂房或仓库的方法，这种方法主要考虑的因素是现有设施之间的距离和要运输的货物量，经常用于中间仓库或分销仓库的选择。商品运输量是影响商品运输费用的主要因素，仓库尽可能接近运量较大的网点，从而使较大的商品运量走相对较短的路程，就是求出本地区实际商品运量的重心所在的位置。

　　The centre-of-gravity method is used to find a location which minimizes transportation costs. It is based on the idea that all possible location have value which is the sum of all transportation costs to and from that location. The best location, the one which minimizes costs, is represented by what in a physical analogy would be the weighted centre-of-gravity of all points to and from which goods are transported.

　　In practice, the optimum location might also be influenced by other factors such as the transportation network. so if the optimum location was at a point with poor access to a suitable road or at some other unsuitable location (in a residential area or the middle of a lake for example) then the location will need to be adjusted.

[编辑]

重心法计算公式

　　重心法首先要在坐标系中标出各个地点的位置，目的在于确定各点的相对距离。坐标系可以随便建立。在国际选址中，经常采用经度和纬度建立坐标。然后，根据各点在坐标系中的横纵坐标值求出成本运输最低的位置坐标X和Y，重心法使用的公式是：

$C_x=\frac{\sum D_{ix}V_i} {\sum V_i}$

$C_y=\frac{\sum D_{iy}V_i} {\sum V_i}$

　　公式中

$C x$ -- 重心的x坐标；
$C y$ -- 重心的y坐标；
$D i x$ --第i个地点的x坐标；
$D i y$ --第i个地点的y坐标；
$V i$ --运到第i个地点或从第i个地点运出的货物量。

　　最后，选择求出的重心点坐标值对应的地点作为要布置设施的地点。

[编辑]

重心法计算的假设条件

　　重心法是在理想条件下求出的仓库位置，但模型中的假设条件在实际会受到一定的限制。重心法计算中简化的假设条件包括以下几方面：

　　⑴模型常常假设需求量集中于某一点，而实际上需求来自分散于广阔区域内的多个消费点。

　　⑵模型没有区分在不同地点建设仓库所需的资本成本，以及与在不同地点经营有关的其他成本的差别，而只计算运输成本。

　　⑶运输成本在公式中是以线性比例随距离增加的，而运费是不随运距变化的固定的部分和随运距变化的可变部分组成。

　　⑷模型中仓库与其他网络节点之间的路线通常假定为直线。而应该选用的是实际运输所采用的路线。

　　⑸模型未考虑未来收入和成本的变化。

　　从以上假设中可以看出模型存在诸多的限制条件，但这也并不意味着模型没有使用价值。重要的是选址模型的结果对事实问题的敏感程度。如果简化假设条件，对模型设施选址的建议影响很小或根本没有影响，那么可以证明简单的模型比复杂的模型更有效。

[编辑]

重心法案例分析

[编辑]

案例一:基于重心法在产品属性最优点选择中的应用^[1]

　　一、引言

　　在消费者市场中,受各种环境因素的影响,使不同消费者对同一产品的需求存在很大差异,形成不同的消费偏好。具有相似或者相近偏好的消费者构成消费者集群,某种产品的消费者市场往往存在若干个消费者集群。产品属性是影响顾客购买行为的重要因素,企业推行无差异营销策略时,就必须把产品的属性定位于某个最优点,使产品最大限度地满足消费者需求,即把所有消费者对产品的不满意程度降到最小。在实务中,企业面对一个存在若干个消费者集群的市场,企业必须寻找产品属性最优点,用同一种符合该属性的产品去满足不同集群消费者的需要,这样比较经济。重心法是单一设施选址常用的数学方法,它将运输成本作为唯一的选址决策依据,以追求配送成本的最小化为目标,寻找最优配送中心。现有的文献对重心法的应用研究仅仅局限在传统的物流选址问题上。尝试在新领域应用重心法,将产品属性最优点定位问题转化为配送中心选址问题,利用重心法确定产品属性最优点,使所有消费者对产品的不满意程度最小,从而为企业在产品设计开发工作中提供一种选择途径。

　　二、模型建立

　　1.模型假设。基于以下假设建立模型：

　　(1)属性A和属性B为某种产品的两个关键属性,对消费者的购买行为产生决定性的影响。令X,Y分别代表消费者对产品属性A和属性B的偏好,所有X与Y的组合可以形成一个连续的二维坐标平面,每个消费者对属性A和属性B的偏好组合可以表示为坐标系 $X 0$ Y中的一个点(X,Y),定义为消费者偏好点。

　　(2)消费者存在差异性偏好,对该产品属性存在相似偏好的消费者构成消费者集群,并且消费者市场存在不同的消费者集群,每个消费者集群对属性A与属性B的偏好组合在坐标平面内形成点集。

　　消费者市场存在4个消费者集群,形成4个消费者偏好点集。用一个最小的圆把每个消费者偏好点集的所有点圈住,令各圆心分别代表消费集群的偏好,定义为消费者集群的偏好中心 $(X i, Y i)$ 。

　　(3)企业在该消费者市场上采用无差异营销策略,只开发一种产品,该产品的属性对应X0Y坐标平面内唯一的点 $(X 0, Y 0)$ ,该点定义为产品中心。

　　2.重心法寻找最优产品中心。由于企业采用无差异营销策略,而消费者存在差异性偏好,因而消费者对该企业的产品属性必然存在不满意。不同消费者集群对产品属性的偏好不同,造成不同消费者集群对产品属性的不满意程度不同。各个消费者集群的不满意程度可以通过一定的方法测出,其测量等价于顾客满意度的测量。顾客满意度可以用等级法进行分级,把顾客满意度分为6级。

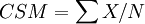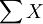　　6个顾客满意度等级：很不满意,不满意,不太满意,较满意,满意,很满意。它们分别赋值0,20,40,60,80,100。顾客的满意度得分为 $CSM=\sum X/N$ ,其中 $\sum X$ 代表调查项目的顾客评分和,N代表调查产品属性的数量。因而,消费者的不满意程度表示为b=100-CSM,b越大,表示消费者对产品的不满意程度越大,反之,则越小。以某产品为例,见下表。

　　某产品的消费者不满意测量表

产品属性	A	B
顾客满意级别	较满意	满意
分值	60	80
消费者不满意度	b=100-CSM=100[(60+80)/2]=30

　　上表展示该产品的调查项目有属性A与属性B,利用公式b=100-CSM求出消费者对该产品的不满意度为30分。

　　企业对产品属性进行定位时,必须找到最优产品属性中心,使得此产品最大限度地满足所有消费者偏好,消费者对该产品总不满意程度最小。此问题转化为配送中心选址问题,利用重心法求出最优产品属性中心。

　　令消费者集群i的偏好中心 $(X i, Y i)$ 与产品属性中心 $(X 0, Y 0)$ 的直线距离为。

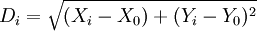　　 $D_i=\sqrt{(X_i-X_0)+(Y_i-Y_0)^2}$ 　　(1)

　　假设在其他条件不变的情况下,消费者集群i对产品不满意程度与距离 $D i$ 成线性关系,距离 $D i$ 越大代表消费者集群对产品不满意程度越大,反之亦然。并假设当 $D i = 0$ 时,消费者集群对产品不满意程度为0。在其他条件不变的情况下,单位距离 $D i$ 代表的不满意程度,定义为消费者集群i的不满意率 $K i$ 。对于某个消费者集群i,其所包含的每个消费者不满意率 $K i$ 相等,但不同的消费者集群i所对应的不满意率 $K i$ 不一定相等。不同的消费者集群对产品的需求量不同,在表示消费者集群对产品不满意程度时,模型需要引入需求量作为影响因素。因而,令消费者集群i对产品的需求量为 $W i$ ,则消费者集群i对产品的不满意程度表示为

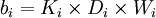　　 $b_i=K_i\times D_i\times W_i$ 　　(2)

　　设某种产品消费者市场存在n个消费者集群,偏好中心为 $(X i, Y i)$ (i=1,2,...,n),该产品的产品属性中心为(X_0,Y_0),则该市场所有消费者集群对该产品的总不满意程度表示为。

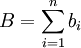　　 $B=\sum_{i=1}^n b_i$ (3)

　　求使B最小的最优产品中心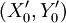 $(X^\prime_0,Y^\prime_0)$ ,则

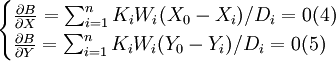
　　 $\begin{cases}\frac{\partial B}{\partial X}=\sum_{i=1}^n K_iW_i(X_0-X_i)/D_i=0(4)\\ \frac{\partial B}{\partial Y}=\sum_{i=1}^n K_iW_i(Y_0-Y_i)/D_i=0(5)\end{cases}$

　　解得最优产品中心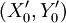 $(X^\prime_0,Y^\prime_0)$ 为

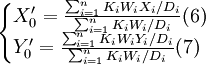　　 $\begin{cases}X^\prime_0=\frac{\sum_{i=1}^n K_iW_iX_i/D_i}{\sum_{i=1}^n K_iW_i/D_i}(6)\\Y^\prime_0=\frac{\sum_{i=1}^n K_iW_iY_i/D_i}{\sum_{i=1}^n K_iW_i/D_i}(7)\end{cases}$ 。

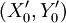　　采用迭代法求出 $(X^\prime_0,Y^\prime_0)$ ,迭代步骤如下：

　　(I)对于式子(6)和式子(7),令 $D i = 1$ ,得到产品中心初始点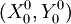 $(X^0_0,Y^0_0)$ ；

　　(II)利用式子(1),式子(3),求出与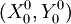 $(X^0_0,Y^0_0)$ 相应的总不满意程度 $B 0$ ；

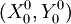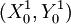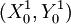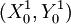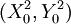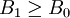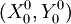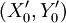　　(III)把 $(X^0_0,Y^0_0)$ 代入式子(1)、式子(6)、式子(7),计算出产品属性中心改善点 $(X^1_0,Y^1_0)$ ；(IV)利用式子(1)与式子(3),计算出与 $(X^1_0,Y^1_0)$ 相应的总不满意程度B'；(V) $B 1$ 与 $B 0$ 比较：如果 $B 1 < B 0$ ,则返回步骤(III),把 $(X^1_0,Y^1_0)$ 代入式子(1)、式子(6)、式子(7),计算出产品属性中心再改善点 $(X^2_0,Y^2_0)$ ；如果 $B_1\ge B_0$ ,则说明 $(X^0_0,Y^0_0)$ 就是最优解。这样反复计算,直到 $B^{k+1}\ge B_k$ 为止,得到 $(X^k_0,Y^k_0)$ 就是最优产品中心 $(X^\prime_0,Y^\prime_0)$ ,此时消费者对产品的总不满意程度最小。

　　在实践中,企业可以在不同情况下利用重心法寻找最优产品中心,对产品属性进行定位,使消费者对产品的总不满意程度最小：

　　(1)如果某种产品尚未处于设计阶段,企业可以通过市场调查,预测消费者集群数目n,每个消费者集群需求量 $W i$ 以及不满意率 $K i$ 。当没有充足的资料预测消费者集群不满意率 $K i$ ,可以认为所有消费者集群的不满意率 $K i$ 相等。企业利用重心法初步求出最优产品属性中心,从而相应地设计开发产品,投入市场测试消费者对产品的反应。通过此方法,企业可以在产品的市场测试阶段,尽量降低消费者对该产品的总不满意程度,初步在消费者市场塑造良好的产品形象。待该产品投入市场一段时间后,重新进行市场调查,反馈测试信息,再相应地根据消费者集群数目n,每个消费者集群i的需求量 $W i$ 及相应的不满意率 $K i$ ,利用重心法求出最优产品属性中心,改进产品的属性,重新把改进的产品推向市场,最大限度地满足消费者的偏好,使消费者对产品的总不满意程度最小。利用重心法对产品属性进行定位,可以避免新产品属性设计开发工作的盲目性,使产品在市场测试期间更好地塑造良好的产品形象,可作为产品属性改进工作的理论依据。

　　(2)如果某种产品早已经投入市场销售,由于市场环境变化,消费者集群数目n、需求量W_i、不满意率K_i等发生变化。企业需要根据市场情况,对产品属性进行适当的调整,则可利用重心法找到最优产品属性中心,作为产品属性重新定位工作的理论参考。

　　三、应用实例

　　某饮料厂生产汽水,已知该种汽水的柠檬酸浓度和糖精浓度对消费者的购买行为产生决定性影响。经过市场调查,发现消费者对汽水柠檬酸浓度和糖精浓度的偏好组合不同,市场存在5个消费者集群,按每500mL汽水含X单位柠檬酸和Y单位糖精计算,消费者集群偏好中心 $(X i, Y i)$ 分别为：(50,45),(30,60),(32,20),(40,30),(20,50)；需求量： $W 1 = 50, W 2 = 80, W 3 = 90, W 4 = 30, W 5 = 75$ ;不满意率： $K 1 = 2, K 2 = 7, K 3 = 5, K 4 = 4, K 5 = 8$ 。

　　企业采用无差异营销战略销售汽水,则按每500mL汽水含X单位柠檬酸和Y单位糖精的组合标准配制汽水,X、Y各为多少时,汽水才能最大限度地满足各个消费者集群的偏好,使得消费者对该汽水的总不满意程度最小？利用重心法寻找汽水的最优产品属性中心,算法如下：对于式子(6)、式子(7),令 $D 1 = 1$ 求出汽水的产品属性中心初始点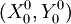 $(X^0_0,Y^0_0)$ ：

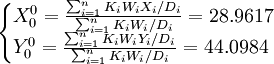
　　 $\begin{cases}X^0_0=\frac{\sum_{i=1}^n K_iW_iX_i/D_i}{\sum_{i=1}^n K_iW_i/D_i}=28.9617\\ Y^0_0=\frac{\sum_{i=1}^n K_iW_iY_i/D_i}{\sum_{i=1}^n K_iW_i/D_i}=44.0984\end{cases}$

　　用迭代法改善该产品属性中心初始点,据式子(1)得 $D 1 = 21.0576, D 2 = 15.9355, D 3 = 24.2891, D 4 = 17.9055, D 5 = 10.7304$ ,因而消费者的总不满意度为：

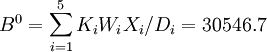
　　 $B^0=\sum_{i=1}^5K_iW_iX_i/D_i=30546.7$

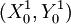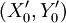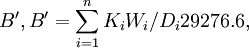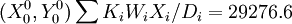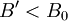　　据式子(1)、式子(6)、式子(7)求出产品属性中心改善点 $(X^1_0,Y^1_0)$ ,得到。(见右)据式子(1)、式子(3),利用 $(X^\prime_0,Y^\prime_0)$ 求出 $D i$ ( $D i$ 的计算结果略)与 $B^\prime,B^\prime={\sum_{i=1}^n K_iW_i/D_i}29276.6,$ 利用 $(X^0_0,Y^0_0)\sum K_iW_iX_i/D_i=29276.6$ ,因为 $B^\prime<B_0$ ,所以初始点(28.9617,44.0984)并非汽水的最优产品属性中心,继续迭代运算。迭代过程不再详述,迭代结果如下表所示。

　　迭代运算结果表

迭代次数j	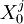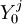$X^j_0$	$Y^j_0$	总不满意度 $B j$
0	2896.17	44.0984	30546.7
1	27.0248	47.0077	29276.6
2	25.8468	48.6027	28812.6
3	25.1104	49.6027	28679.3
4	24.6479	49.5103	28679.3
5	24.3434	49.5766	28622.1
6	24.1324	49.5934	28614.0
7	23.9811	49.5977	28607.3
8	23.8700	49.5994	28607.3
9	23.7872	49.6007	28605.9
10	23.7246	49.6019	28605.2
11	23.6404	49.6030	28604.7
12	23.6404	49.6040	28604.4
13	23.6122	49.6048	28604.3
14	23.5903	49.6055	28604.2
15	23.5734	49.6060	28604.1
16	23.5602	49.6064	28604.1
17	23.5499	49.6068	28604.0
18	23.5418	49.6071	28604.0
19	23.5355	49.6073	28604.0

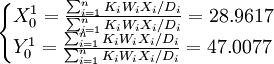　　 $\begin{cases}X^1_0=\frac{\sum_{i=1}^n K_iW_iX_i/D_i}{\sum_{i=1}^n K_iW_iX_i/D_i}=28.9617\\ Y^1_0=\frac{\sum_{i=1}^n K_iW_iX_i/D_i}{\sum_{i=1}^n K_iW_iX_i/D_i}=47.0077\end{cases}$ 。

　　从上表发现,随迭代次数增加,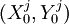 $(X^j_0,Y^j_0)$ 不断地向汽水的最优产品属性中心调整,消费者的总不满意度不断减少。从迭代次数17开始,消费者的总不满意程度达到最小值28604.0,并保持不变,满足 $B k + 1 = B k$ 。所以迭代到第17次时,开始找到汽水的最优产品属性中心(23.5499,49.6068)。因而该企业生产汽水,按每500mL汽水含23.5499单位柠檬酸和49.6068单位糖精的组合标准配制,消费者的总不满意程度达到最小值28604.0。通过此实例分析,说明基于重心法寻找产品属性最优点的理论方法具有实用意义。

　　把一个推行无差异营销策略的企业寻找产品属性最优点问题转化为配送中心选址问题,以消费者的总不满意程度最小为决策依据,利用重心法求出产品属性的最优点。通过实例分析,指出该方法具有实用意义。但把只有两种关键属性的产品作为研究对象,至于具有两种以上关键属性的产品属性最优点问题有待进一步研究。

[编辑]

案例二:重心法在光电信号处理中的应用^[2]

　　一、引言

　　在国家大型项目LAMOST(Large Sky Area Multi-Object Fiber Spectroscopy Telescope,大天区多目标光纤光谱天文望远镜)预研中,为了标定4000根光纤在焦平面上的位置,采用线阵CCD传感器去扫描从光纤中出来的光斑。要较为精确地得到光斑的位置及其在移动时变动的距离,找出光信号上某一位置稳定点是关健。以线阵CCD采集到的光纤出射光斑中某一截面上的信号为例说明在寻找稳定点中与常用的最大值法和截止电压法相比,重心法具有重复精度高,稳定性好等优点。

　　二、常用方法

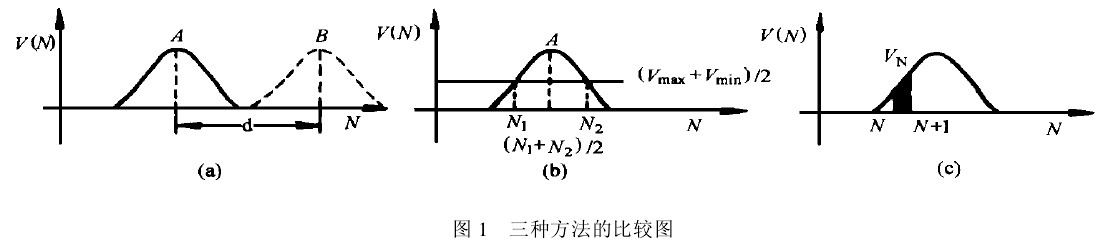
　　用线阵CCD采集到的光纤出射光斑的某一截面形状如图1所示。N为采样次序,V(N)为与采样次序相对应的电平。

　　1.最大值法

　　对于如图1(a)所示信号,找出其最大值A点。

　　2.截止电压法

　　如图1(b)所示,用截止电压V=k1Vmax+k2Vmin去截信号,求得N1,N2两点。其中k1=k2=0.5,此时在截止电压V与曲线的交点附近曲线较陡,测量值的变化量较小,测量的稳定性好。取与(N1+N2)/2相对应的点A作为信号的代表点。

　　三、重心法

　　重心法是对信号进行面积分,积分区域取与截止电压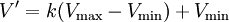 $V^\prime=k(V_\max-V_\min)+V_\min$ 相对应点之间的区域,实验显示,当k=0.1时,x值及其12次重复采样的偏差σ与在整个信号积分时相差不大。当k>0.1且不断增加时,x值的不稳定性和偏差σ显著增加。如图1(c)所示,其中第N区域的面矩为 ${V_N[(N+1)-N]}\cdot N$ ,面积因此采样到的每两个点对应着一个CCD像元,即CCD的每个像元被连续采样两次。即

为 $V N [(N + 1) - N]$ ,求出整个信号的重心 $N A$ 为。

　　 $N_A=\frac{\sum{V_N[(N+1)-N]}\cdot N}{\sum V_N[(N+1)-N]}=\frac{\sum V_N\cdot N}{\sum V_N}$

　　四、实验装置及原理

　　实验装置图如图2所示

　　1—精密水平移动工作台,精度为0.2μm;2—线阵CCD;3—CCD驱动扳;4—放大滤波电路;5—A/D转换及接口板;6—486微机;7—示波器;8—光纤;9—点光源装置,采用卤钨灯作为发光器件。

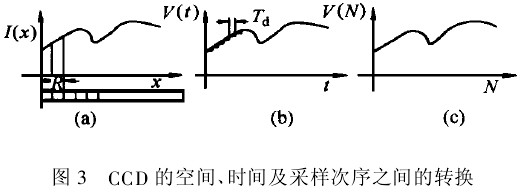
　　CCD为光电转换装置,将接收到的空间光强分布转换为随时间变化的电压信号,如图3(a)和图3(b)所示,其转换关系为。

　　 $\frac{x}{R}=\frac{t}{T_d}$ 　　(1)

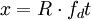　　 $x=R\cdot f_dt$ 　　(2)

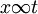　　 $x\infty t$ 　　(3)

　　 $x=\frac{13\cdot N}{2}=6.5N(\mu m)$ 　　(4)

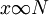　　 $x\infty N$ 　　(5)

　　如图3(c)所示。

　　当信号沿图2中x方向移动一段距离时(在本实验中光纤不动,CCD固定在水平移动工作台上并随其一起动):

　　 $d = X B - X A = 6.5(N B - N A)$ 　　(6)

　　如图1(a)所示。

　　其中fd(=1/Td)为CCD驱动频率;R为光敏单元的几何尺寸。

　　在本实验中采用的CCD型号为TH7805A,有效感光像元数为2048个,像元尺寸为13μm×13μm,R=13μm,工作时采用的驱动频率为500kHz。

　　信号处理过程如图4所示。

　　在实验系统中低通滤波的截止频率为2kHz,高通滤波的截止频率为13Hz。A/D转换器为MAX118C,其采样频率为1MHz。

　　五、实验结果

　　表1 三种方法的σ值比较

σ/μm
距离L/mm	5	10
最大值法	34.13-84.18	92.37-199.68
截止电压法	0-5.66	8.06-32.63
重心法	0.46-0.91	1.37-4.03

　　表1为当CCD像元表面与光纤端面之间距离L分别约为5.0mm,10.0mm, CCD位置沿图2中x方向水平移动时,通过21次单次测量,每次测量重复采样12次的三种方法的x均方很差值σ。由表1可见,当L=5mm时,重心法的偏差σ最小,在1μm以内,而且随着L的增加,其它两种方法的σ剧增,而重心法的σ变动较小。由此可见,尽管该CCD本身像敏单元的几何分辨力只有13μm,通过重心法可使信号的位置偏差保持在1μm以内。

　　三种方法的d值比较

　　在图5中,图5(a)为图2中L约为5.0mm时,水平移动工作台沿x方向每移动2mm,按公式(6)求得d的测量结果。图5(b)为L增加至10.0mm时测量的结果。其中虚线1为最大值法结果,双点划线2为截止电压法结果,实线3为重心法结果。在CCD两端处d值波动较大。

　　在图5(a)中,用重心法测得的d值在1.990~2.010mm之间,变化在±10μm以内,其中包括水平移动工作台本身的系统误差及读数的偶然误差。随着沿z方向距离的增加,重心法的稳定性显然最好。但重心法也存在缺点,若CCD感受不到完整的信号或所选取的信号积分区域太窄,其误差将显著增加。信号信噪比越高,光信号落在CCD像敏单元上的范围越小,其效果越好。在本实验中,这与CCD与光纤端面之间的距离、光纤的数值孔径、光源的强弱、光源与光纤之间的光耦合等因素有关。

　　六、分析及结论

　　从微观上来看,从CCD出来的电信号是一个个幅值不同的脉冲,一个像元对应着一个脉冲,如图2(b)所示。设理想采样,由于每个像元被采样两次,当用最大值法时,采得最大幅值电压脉冲上某点为最大值点,那么在下次或前次采样时,采样点可能同样落在该电压脉冲上。此外存在光响应的非均匀性,在某些像元上缺陷密集而形成暗电流尖峰以及受A/D转换的精度限制。

　　因此与最大值对应的点就不是唯一的且采样点本身的不确定度为6.5μm。当用截止电压法时,与截止电压相对应的点同样存在以上现象。但由于对选取的两点进行了平均,可以抵消部分不确定度。重心法是对区域信号求面积的矩,然后再在区域内作面积平均,对将近4000个点进行了加权平均,可显著降低每个点对整个信号的影响,有利于消除系统误差,减小随机误差,提高值的稳定性和重复精度。事实上,由于系统本身存在光源电压的波动,CCD光敏单元的不均匀性,CCD中的暗电流和电噪声,电路的温漂等和周围工作环境如杂散光的影响,所以重复采集到的信号总存在着漂移和随机干扰,这就更增加了最大值法和截止电压法的不稳定性。

　　在LAMOST项目中是针对光纤出射光进行研究的,其在空间呈二维分布,虽然在这里讨论的只是一维方向的问题,但重心法同样可以应用到二维光信号的处理。

　　重心法还可以推广到对不规则信号及多峰信号进行类似的处理。

[编辑]

参考文献

↑ 许露.基于重心法在产品属性最优点选择中的应用[J].经济师,2009,(5)
↑ 李静,李为民,陈晓东等.重心法在光电信号处理中的应用[J].光学技术,1999,(2)

来自"https://wiki.mbalib.com/wiki/%E9%87%8D%E5%BF%83%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

蔓草寒烟,Dosgame,苦行者,Vulture,sky,Kane0135,Angle Roh,Zfj3000,Cabbage,Fghghg,Dan,连晓雾,Lin.

页面分类: 选址方法

评论(共2条)

提示:评论内容为网友针对条目"重心法"展开的讨论，与本站观点立场无关。

183.61.11.* 在 2014年4月16日 19:13 发表

　　　　重心法还可以推广到对不规则信号及多峰信号进行类似的处理。

回复评论

117.136.92.* 在 2016年11月14日 09:42 发表

看不懂

回复评论

发表评论请文明上网，理性发言并遵守有关规定。

查看

工具箱▼

重心法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么叫重心法?

重心法计算公式

重心法计算的假设条件

重心法案例分析

案例一:基于重心法在产品属性最优点选择中的应用^[1]

案例二:重心法在光电信号处理中的应用^[2]

参考文献

温馨提示

本条目相关课程

本条目由以下用户参与贡献

评论(共2条)

导航

意见反馈

查看

工具箱▼

重心法

出自 MBA智库百科(https://wiki.mbalib.com/)

目录

什么叫重心法?

重心法计算公式

重心法计算的假设条件

重心法案例分析

案例一:基于重心法在产品属性最优点选择中的应用[1]

案例二:重心法在光电信号处理中的应用[2]

参考文献

温馨提示

本条目相关文档

本条目相关课程

本条目由以下用户参与贡献

评论(共2条)

导航

意见反馈

案例一:基于重心法在产品属性最优点选择中的应用^[1]

案例二:重心法在光电信号处理中的应用^[2]