逻辑思维的基本规律
出自 MBA智库百科(https://wiki.mbalib.com/)
- 该条目对应的页面分类是逻辑思维的基本规律。
目录 |
逻辑思维的基本规律概述 [1]
亦称“思维基本规律”,即同一律、矛盾律、排中律,以及由莱布尼茨所提出的充足理由律,它们构成了理性思维最基本的前提与预设,是理性的对话、交谈能够进行下去的最起码前提,分别确保理性思维具有确定性、一致性、明确性和论证性。
不过,关于充足理由律是不是逻辑基本规律,存在着不同的争论意见,并且占主导地位的意见似乎认为它不是逻辑基本规律。本书倾向于把它当作基本规律来对待。
其内容是:在同一思维过程中,一切思想(包括概念和命题)都必须与自身保持同一。可用公式表示如下:
A是A;或者,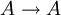
这里,“A”指在思维过程中所使用的任何一个概念或命题。
同一律的作用在于保证思维的确定性,以便人们之间的思想交流能够顺利进行。
如果违反同一律在概念方面的要求,就会犯“混淆概念”或“偷换概念”的逻辑错误。
如果违反同一律在命题和论辩方面的要求,就会犯“转移论题”或“偷换论题”的错误。
应该叫做(不)矛盾律。其内容是:两个互相矛盾或互相反对的命题不能同真,必有一假。可用公式表示如下:
并非(A并且非A);或者,
这里,“A”代表一个命题,“非A”代表A的否定命题,或是蕴涵A的否定的命题,所以这里的“ ”既包括与A互相矛盾的命题,也包括与A互相反对的命题。
”既包括与A互相矛盾的命题,也包括与A互相反对的命题。
矛盾律的作用在于保证思维的一致性,即无矛盾性。
违反矛盾律的要求,就会犯“自相矛盾”的逻辑错误。
其内容是:两个互相矛盾的命题不能同假,必有一真。可用公式表示如下:
A或者非A;或者,
这里,“A”代表一个命题,“非A”则只代表与A互相矛盾的命题,A和非A之间必须既不能同真,也不能同假。
排中律的逻辑要求是:对两个互相矛盾的命题不能都否定,必须肯定其中一个,否则会犯“两不可”的错误。
排中律的作用在于保证思维的明确性。
违反排中律会犯“模棱两可”或“两不可”的错误。
矛盾律和排中律的内容一起构成所谓的“二值原则”:任一命题或者是真的或者是假的,不能既真又假,也不能既不真也不假。这就是说,非真即假,非假即真。
二值原则刻画了日常所使用的“真”、“假”这两个概念的特征,它们是以实在论为基础的:任一命题都是在述说关于独立于该命题的某种客观实在,这种客观实在决定着该命题的真或假。因此,描述外部实在的任何一个命题都有一个确定的真值:真或者假,而不依赖于人们是否知道这一点,甚至不依赖于人们是否有可能知道这一点。
一般使用的逻辑都是建立在二值原则之上的,因此叫做“二值逻辑”。
其内容是:在同一思维和论证过程中,一个思想被确定为真,要有充足的理由。可用公式表示如下:
这里“├”表示“推出”,上面的公式有两种解读方式:
- 如果要证明B是真的,必须先证明A是真的,并且证明从A能够逻辑地推出B。
- 或者,如果要证明B是某系统的定理,必须先证明A是该系统的定理,并且证明从A能够逻辑地推出B。
充足理由律的具体要求是:
- 对所要论证的观点必须给出理由;
- 给出的理由必须真实;
- 从给出的理由必须能够推出所要论证的论点。
否则,就会犯“没有理由”、“理由虚假”和“推不出来”的错误。
充足理由律的作用在于确保思维的论证性。
逻辑思维的基本规律[2]
同一律的内容是:在同一个思维过程中,反映同一个对象的思想是确定的,必须始终保持同一个含义,不能偸换它的含义。
同一律要求思维必须具有确定性。
就命题而言,同一律要求,一个命题如果代表的是某个事件,它就必须始终代表这一事件。如果这一事件是事实,那么该命题就是真的;如果命题代表的事件不是事实那么命题就是假的。因此同一律认为,一个命题必须有确定的真值,如果是真的那么它就是真的,如果是假的那么它就是假的。这一要求我们可以用“p→p”表示。
就词项而言,同一律要求,一个词项如果指称某个对象,它就必须始终指称这个对象。就是说词项a就是a,它具有确定的外延和内涵,并始终保持同一的外延和内涵,即保持自身同一。这一要求可用公式“a=a”表示。
违反同一律的要求,就会产生逻辑错误。这样的逻辑错误主要有两个方面:
- 1、混淆词项,又叫作混淆概念的逻辑错误
语词具有多义性,一个语词一般来说同含义、对象之间并无一一对应关系。同一语词往往可以表达多种不同的含义,指称多种不同的对象,这就是语词的多义性与歧义性,它导致了语词相同但表达的词项不同的现象,使混淆词项、混淆概念等逻辑错误的产生成为可能。
我们把那些在同一思维过程中,不加说明、定义地用同一个语词项表达不同的含义,指称不同的对象所犯的逻辑错误,称为混淆词项、混淆概念。以同一字眼或同一语词表达不同的词项,或者说赋予同一语词以不同的含义是这种逻辑错误的典型表现。
如在《韩非子》中有这样一则故事:郑县有一位姓卜的,他常常在外鬼混。一天他的裤子弄出了一个洞。他买了新布,回家让妻子为他作一条新的裤子。妻子问他如何做,他说“照原样”。于是他妻子把裤子照原来的样式做好后,照样在裤子原来的地方剪了一个洞。这当然是一个笑话。但从逻辑的角度来说,他的妻子是有意或无意地违反同一律。“原样”在丈夫的那里指的是原来样式的、尺寸,绝不是有破洞的原样。
在使用语词表达词项、指称对象时,如果是无意地违反了同一律的要求,所犯的错误就称为“混淆词项”或者“混淆概念”。如果是故意违反同一律要求以达到某种目的,就称为“偷换词项”或者“偷换概念”。两者的区别只在违反同一律的动机上而并不在形式上。
- 2、混淆论题的逻辑错误
在没有语境限制的情况下,同一语句可以陈述不同的内容,即它表达的涵义有可能是不相同的,这就是语句的歧义性。这就使“混淆论题”逻辑错误的产生成为可能。我们把那些在同一思维过程中用一个似是而非的论题来代替原来的论题的现象称作“混淆论题”的逻辑错误。
例如,鲁迅在其杂文里曾经谈论到一位不懂逻辑的排长。他写道:“这排长的天真,…他以为不抵抗将军下台,‘不抵抗’就一定跟着下台了。这是不懂逻辑:将军是一个人,而不抵抗是一种主义,人可以下台,主义却可以仍旧留在台上的。”(《鲁迅全集》第5卷第116页)鲁迅提到的这位天真的排长所以错误,就在于他把“不抵抗将军下台”和“不抵抗主义下台”混为一谈,违反了同一律的要求犯了“混淆论题”的逻辑错误。
不自觉地或者无意地以一个似是而非的论题来代替原论题的,称为混淆论题。但如果别有所图而故意违反同一律要求混淆论题的称为“偷换论题”的逻辑错误。
同一律从形式上说,只是关于逻辑形式表述思维时应当遵守的规律。只有遵守同一律的要求,才能使思维在表述上具有确定性。因此可以说,遵守同一律是人们正确认识事物的必要条件,它要求我们在表述思维的同一过程中,任何一个词项都要前后一致地保持含义即内涵的相同,并且使指称对象即外延也相同,否则,我们在词项的理解上就要发生混乱;任何一个命题都要前后一致地保持意义即内容上的相同和在真假断定上的相同, 否则,我们在命题的理解上就要发生混乱。 词项或命题在理解上的混乱,都将导致思维本身的混乱,从而不可能去正确地进行思维以真实地认识客观世界。不能准确无误地去表达、交流思想,也就不可能在思想交流的过程中及时地发现、揭露和反驳谬论或诡辩。
说遵守同一律是正确地表达思维的必要条件,是说违反了同一律,对思维的表达必定是错误的,但遵守了同一律,对思维的表达也未必一定是正确的。例如,在“教育是有阶级性的,教育是社会现象,所以,社会现象是有阶级性的”这一推论过程中所表现出来的思维活动,检查其使用的词项和命题,一般来说都被认为是遵守了同一律的,但这个推理活动仍然是错误的。因此,我们应当恰如其分地而不是夸大地把握同一律的认识作用。
说遵守同一律是正确地表达思维的必要条件,还强调着同一律只是在人们运用逻辑形式的过程中起作用的规律,它作用的对象仅仅是人们所使用的逻辑形式,是运用逻辑形式的规律,这显然有别于我们常说的客观世界本身的规律。因此不能把人们对事物的不同观点、不同理解,以及运用词项表示发展并丰富起来的概念、运用命题对同一事物从不同的角度所陈述的不同观点等等都看成是对同一律要求的违反。这也就是说,不能把同一律和形而上学的世界观一概而论。同一律既不否定客观世界本身的运动性、发展性、丰富多彩性,也不排斥人们在认识客观世界是所持有的辩证唯物主义的观点。
矛盾律也称为不矛盾律。它的内容是:在同一思维过程中,关于同一对象的思想必须始终保持一致,不能自相矛盾。
矛盾律要求思维必须具有一致性。
就命题而言,由于在同一时间同一关系上一个事件不可能即存在又不存在,因此我们不可能对同一命题作出不同的断定,不能既断定它真,又断定它假。由此矛盾律要求:两个互相否定的命题不可能都真,必有一个是假的。矛盾律的这一要求可用公式“?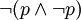 ”表示.。例如,我们不能既断定“这个证人的所有话都是真的”,同时又断定“这个证人的有些话不是真的”。
”表示.。例如,我们不能既断定“这个证人的所有话都是真的”,同时又断定“这个证人的有些话不是真的”。
就词项而言,同一律的要求可用公式“a ≠ a ”表示。即要求不能用两个相互的否定的词项指称同一个对象,并且同一个词项不能包含自相矛盾的东西。例如,“方的圆”、“可以溶化一切的溶液”等都是违反矛盾律的。
逻辑矛盾是在同一思维过程中对同一对象做出互相否定的表述时所产生的逻辑错误。如上所述,互相否定的表述形式可分为相互矛盾的命题和相互反对的命题,因此违反矛盾律的逻辑错误尽管我们都把它称为“自相矛盾”,但在应用时则应分为两种情况去处理。
首先,是在同一思维过程中对一对矛盾命题的表述同时予以肯定或者否定而产生的逻辑错误。矛盾命题在真或者假上总是不相容的,我们既不能同时断定它们都真,也不能同时断定它们都假。不妨以命题形式p→q和~(p→q)为例,它们的真值表分别是
- p→q ~(p→q)
- TT T F TT T
- TF F T TF F
- FT T F FT T
- FT F F FT F
显然,在对命题形式赋值的同一过程中, p→q和~(p→q)的真值在任何条件下都是既不同真也不同假的。它表明,只要我们肯定p→q就要否定~(p→q),而否定p→q就要肯定~(p→q),反之亦然。在传统逻辑中,把违反矛盾律的要求,在同一思维过程中同时肯定或否定一对矛盾关系的命题产生的错误称为“自相矛盾”,我国先哲韩非子在《韩非子?难一》中所讲的一个寓言故事,最为生动地反映了自相矛盾的这种错误。该故事描写了的一个既卖矛又卖盾的楚国人,他吹嘘自己的矛是世界上最为锋利的,以至于“任何东西都能被它扎透”;继而,他又炫耀自己的盾,是世界上最为坚固的,是“没有任何东西能扎透它的”。旁边有好事者问他,“若以你的矛扎你的盾,其结果又如何呢?”这个卖矛又卖盾的楚国人只好张口结舌,无以为答了。其所以不能对答,就在于他在宣传自己的矛与盾的过程中所陈述的两个命题“任何东西都能被它扎透”和“没有任何东西能扎透它的”,它们构成了一对逻辑矛盾,因而犯了“自相矛盾”的逻辑错误。
我们在说话、写文章等等过程中,如果不注意思想的前后一贯性,就可能出现逻辑矛盾。例如,有人说:“实践是检验真理的唯一标准,但马克思列宁主义也是检验真理的标准”这肯定是自相矛盾的。因为既然说前者是“唯一的”,那么其他的标准又从何而来呢?又如“大家相互作了自我批评”,显然,是“自我批评”就不是“相互”的,而是“相互”的也决不是“自我批评”,尽管这里只出现了一个命题,但却是一个自相矛盾的命题。
其次,违反矛盾律的错误,是在同一思维过程中对一对表述反对关系的命题同时予以肯定而产生的逻辑错误。把在同一思维过程中对一对表述为反对关系的命题同时予以肯定依旧归结为“自相矛盾”,这是符合矛盾律的要求的,因为具有反对关系的一对命题本质上是相互否定的,在同一思维过程中对它们都肯定显然是错误的。但是,矛盾律对具有矛盾关系和反对关系的命题在如何制约上是有区别的。对矛盾关系的命题来说,矛盾律肯定其一真一假,当其中一个命题为真时,另一个命题则必然是假的,反之亦然;而对具有反对关系的命题来说,矛盾律尽管可以由其中一命题的真肯定另一命题的假,但反之却不成立,因为具有反对关系的命题是可以同假的。我们以命题形式p∧q与p∧~q的真值表来比较说明。
- p∧q p∧~q
- TT T TF F T
- TF F TT T F
- FF T FF F T
- FF F FF T F
从上述真值表的第二、五两列可以看出,虽然p∧q取真时p∧~q必然取假, p∧~q取真时p∧q必然为假,但当p∧q取假时, p∧~q是可以同时为假的,反之也一样。这表明,当矛盾律作用的对象是具有反对关系的一对命题时,我们不能由其中的一个命题假去推断另一个命题的真。
遵守矛盾律的要求,同样是思维得以正确表达的必要条件。换言之,只有遵守了矛盾律的要求,思维在由逻辑形式的表述过程中才能首尾一贯,前后一致,表达准确。而违犯矛盾律的要求,在思维的表达上必然是相互矛盾的,因此,最终导致思维也是混乱的。例如,如果我们在同一时间去既肯定命题“我们班的同学现都在军训”,又肯定命题“我们班第一小组的同学现正在上心理学课”,这就违反了矛盾律的要求,在命题的表述上是自相矛盾的。但如果我们同时肯定“我们班有的同学是党员”和“我们班有的同学是非党员”,尽管此时的谓项是一对具有矛盾关系的词项,但两个命题既无脑袋关系又无反对关系,因此并不违犯矛盾律的要求。矛盾律也是我们进行反驳的一个重要理论依据,人们在反驳一个假命题时,常常是间接地去证明这个假命题的矛盾命题或反对命题为真,从而根据矛盾律去说明原命题的假。而在确立某个命题的真时,也可以去证明该命题的矛盾命题的假, 从而根据矛盾律去说明原命题的真,但此时应当注意的是,所涉及的两命题现在必须是矛盾关系而不是反对关系。
排中律的内容是:在同一思维过程中,关于同一事物的两个相互矛盾的思想不可能都是假的,必有一个为真。因此,对于两个互相矛盾的命题,我们必须作出明确的选择.必须肯定其中之一为真。排中律的这一要求可用公式“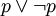 ”表示。
”表示。
要注意,根据排中律的内容,排中律适用于“两个相互矛盾的思想”,这与矛盾律适用“两个相互否定的思想”有所不同。排中律所适用的一般来说是具有矛盾关系的命题。但也有一些特殊情况。如具有下反对关系的两个命题,由于它们不可能都假,因此也必须断定其中一个为真。
例如命题“这个报告提供的数据有些是真实的”与“该报告提供的数据有些不是真实的”,这两个命题不可能都是假的,必有一个为真。我们否定其中的一个真,就必须肯定另一个为真。而具有形式“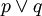 ”与“?
”与“?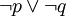 ”的两个命题也是如此。
”的两个命题也是如此。
在同一思维过程中,如果对表述的两个互为矛盾的命题,或者两个具有下反对关系的命题,既不肯定这个,又不肯定那个就要违反排中律的要求。违反排中律的要求而产生的逻辑错误,称为“模棱两可”或“模棱两不可”。
例如,历史上托洛茨基在混布尔什维克党的时候,对自己过去那些反对党的思想所作的声明“我加入布尔什维克党这件事实本身…,已经证明,我已经把过去所有那些使我和布尔什维主义分开的东西放在党的门口了”。托洛茨基既不说“把过去所有那些使我和布尔什维主义分开的东西”抛掉了,也不说对那些东西不抛掉,而只是给出一个含糊不清词项“放在党的门口”,这样的表述就违反了排中律的要求,犯有“模棱两可”的逻辑错误。这是一种以含混的语句违反排中律的方式。又如有人陈述自己的思想说,“说任何事物都不是绝对静止的,这我不同意。但说有的事物是绝对静止的,恐怕也不正确”。这种说法,显然是对“任何事物都不是绝对静止的”和“有的事物都是绝对静止的”这两个矛盾命题的同时否定,当然是违反排中律,犯有“模棱两不可”的逻辑错误。应当注意的是,在排中律的实际运用中,对具有矛盾关系的两个命题固然可以由肯定推否定,并且由否定推肯定,但对具有下反对关系的命题,却只能由否定推肯定,而不可由肯定去推否定。
排中律的作用在于保证思维表述的明确性。只有遵守排中律的要求,才能正确地进行思维表述, 才能正确地进行思维。因此,排中律是正确思维的必要条件。此外,排中律也是间接论证的逻辑依据,当我们难以从正面去证明某个命题时,常常可以通过证明该命题的矛盾命题或具有下反对关系的命题为假,从而由不能都假的特征推出原命题的真。
要正确地运用或理解排中律,应当注意下述几点。
首先,从形式上说,排中律仅仅是正确的思维表述从而是正确思维的必要条件。因此,遵守了排中律的要求,思维表述从而思维本身也仅仅是可能正确的,其最终是否正确还要取决于正确思维的其它必要条件。
其次,排中律同逻辑形式的其它基本规律一样,都是在一定的条件才能产生影响的。固然每一条基本规律都有自己特殊的条件,但决不可以此忽略它们的共有前提,即同一时间、同一场合、同一关系、同一对象等等这些反映同一思维过程的因素。
第三,排中律反映的是思维表述的方法而不是世界观,因此,排中律并不否认客观事物本身状态的多样性,排中律所要排除的,只是人们在思维表述上的居中骑墙,模棱两可,使我们关于对象某一方面的思想表述成为明确的表述。
第四,排中律在其实际应用中,对那些因客观或主观条件尚不成熟,因而不能断定的问题,并不排除采取“二不择一”的表述方式。所谓客观条件不成熟,是指认识对象还处于发展变化的过程中,人们从某一角度对其认识因此还不可能有定论。例如对“非典”的预防,我们对命题“非典的预防有特效药或者没有特效药”的任何一支,都不能如排中律所要求那样作出明确的回答,但此时的“二不选一”的回答是并不违反排中律的。 所谓主观条件不成熟,是指认识对象的发展变化虽然已处于相对静止的阶段,事物本身的属性、与其他事物之间的关系等等都已经是可以确定的了,但人们本身的认识水平并没有跟上事物的发展,人们对事物的认识还处于不能断定的状态。例如,对“火星上有生命还是无生命?”的回答,它实际上涉及到对命题“火星上有生命或者无生命”支命题的选择,当然是一个涉及排中律的问题。但这里的回答却不能简单地是“有”或者“没有”,因为从主观来说,火星的情况虽说是处于相对稳定的阶段,但人们的认识水平则因科学技术的限制尚不能达到对火星真实情况的认识,所以在上述问题的回答中我们只能“二不选一”
最后,排中律在复杂问语的处理上是没有制约作用的。所谓复杂问语,是在疑问句中隐含了某种假设的问句,如“你杀了他是不是心里特高兴?”此时,无论是回答“是”还是“不是”,你都实际上承认了那个隐含的假设即“你杀了他”。。对这样的问句,我们避开问题的肯定和否定,而针对问题中的假设予以说明,就不能说是违反了排中律。
反证法(又称归谬法、背理法)是一种论证方式,他首先假设某命题不成立(即在原命题的条件下,结论不成立),然后推理出明显矛盾的结果,从而下结论说原假设不成立,原命题得证。
反证法常称作Reductio ad absurdum,是拉丁语中的“转化到不可能”,源自希腊语中的“ἡ εις το αδυνατον παγωγη”,阿基米德经常使用它。
“欧几里得最喜欢用的反证法,是数学家最精良的武器。它比起棋手所用的任何战术还要好:棋手可能需要牺牲一只兵或其他棋,但数学家用的却是整个游戏。”《一个数学家的辩解》,英国数学家高德菲·哈罗德·哈代。
维也纳的科学哲学家卡尔·波普尔的论点:“不能被反证的理论就不能被称作科学的理论”。(这里的反证不是指反证法,而是指推翻如证伪、修正、提出异议等。
反证法在数学中经常运用。当论题从正面不容易或不能得到证明时,就需要运用反证法,此即所谓"正难则反"。牛顿曾经说过:“反证法是数学家最精当的武器之一”。一般来讲,反证法常用来证明正面证明有困难,情况多或复杂,而逆否命题则比较浅显的题目,问题可能解决得十分干脆。应用反证法的是:欲证“若P则Q”为真命题,从相反结论出发,得出矛盾,从而原命题为真命题。
反证法是“间接证明法”一类,是从反方向证明的证明方法,即:肯定题设而否定结论,从而得出矛盾。法国数学家阿达玛(Hadamard)对反证法的实质作过概括:“若肯定定理的假设而否定其结论,就会导致矛盾”。具体地讲,反证法就是从反论题入手,把命题结论的否定当作条件,使之得到与条件相矛盾,肯定了命题的结论,从而使命题获得了证明。 在应用反证法证题时,一定要用到“反设”,否则就不是反证法。用反证法证题时,如果欲证明的命题的方面情况只有一种,那么只要将这种情况驳倒了就可以,这种反证法又叫“归谬法”;如果结论的方面情况有多种,那么必须将所有的反面情况一一驳倒,才能推断原结论成立,这种证法又叫“穷举法”。
原理1:给出命题P和命题(非P),根据排中律( ),两者之中起码有一个是真(更强的说法为,除了真和假之外并无其他的情况),所以若果其中一个是假的,另一个就必然是真。
),两者之中起码有一个是真(更强的说法为,除了真和假之外并无其他的情况),所以若果其中一个是假的,另一个就必然是真。
原理2:给出命题P和命题(非P),根据无矛盾律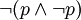 ,两者同时为真的情况
,两者同时为真的情况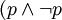 )为假。形式化为:
)为假。形式化为: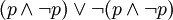 。与排中律的逻辑结构相同。
。与排中律的逻辑结构相同。
原理3:给出命题p和r,根据否定后件律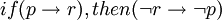 ,如果若成立p时出现r,则为r假时即为p假。
,如果若成立p时出现r,则为r假时即为p假。
反证法在要证明时,透过显示出若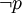 成立时出现矛盾,即为
成立时出现矛盾,即为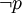 假,从而证明为P真。
假,从而证明为P真。
证明:命题P为真
详细论证以下命题为真:
A.沉默是金
B.和气生财
- 1.反命题为:话多是金。假设该命题为真。
- 2.举出实际反例:
a.言多必失,祸从口入。话过多,把自己底牌亮出,让自己处于信息不对称的地位,暴露自己的隐私与弱点,陷入被动的境地,极易破财。
b.话多误事,分散注意力,效率低下,浪费时间与精力,等同于破财。不节制说话的话,会忘记该做的事情。
c.话多容易造成重复啰嗦甚至伤害人,十分讨人厌,搞坏形象与人缘,等同于甚至甚于破财。一个只知道话多的人,他的思想是不会随着话多而增加的。
d.即使是有些靠说话谋生的人,也不能话多。如,主持人,销售员等,主要靠提问引导对方多说话而不是自己多说话。
e.话多不如话少,话少不如话精。人的内心是很隐密的,恭维了某个人可能就得罪了另一个人。 说话是门艺术,除了十分用脑,还要十分用心。心直口快,小事冒烟,大事冒火,是十分不用脑,十分不用心的表现,也是还没学会自我控制的表现,最终吃亏的就是自己。
f. 实证分析一下:冷静想想身边熟悉的人。话多财多,话多破财,闷声发财,闷声破财。从人数和财富的数量上,对比这四种人中,有没有典型代表,结论自然就能得出。
- 3.反命题:话多是金。该命题不成立。
- 4.据排中律:沉默是金。
- 5.和气生财,大致同理。

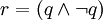 。据
。据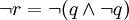








反证法的实际应用
详细论证以下命题为真:
A.沉默是金
B.和气生财
a.言多必失,祸从口入。话过多,把自己底牌亮出,让自己处于信息不对称的地位,暴露自己的隐私与弱点,陷入被动的境地,极易破财。
b.话多误事,效率低下,浪费时间与精力,等同于破财。不节制说话的话,会忘记该做的事情。
c.话多容易造成重复啰嗦甚至伤害人,十分讨人厌,搞坏形象与人缘,等同于甚至甚于破财。
d.即使是靠说话谋生的人,也不能话多。如,主持人,播音员,销售员,等,主要靠提问引导对方多说话而不是自己多说话。