连续性变量风险型决策
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
(重定向自连续性变量的风险型决策)
目录 |
[编辑]
连续性变量的风险型决策方法是解决连续型变量，或者虽然是离散型变量，但可能出现的状态数量很大的决策问题的方法。连续性变量的风险型决策方法可以应用边际分析法和标准正态概率分布等进行决策。
方法的思想：设法寻找期望值作为一个变量随备选方案依一定次序的变化而变化的规律性，只要这个期望值变量在该决策问题定义的区间内是单峰的，则峰值处对应的那一个备选方案就是决策问题的最优方案。这个方法类似于经济学中的边际分析法。
边际利润：指存有并卖出一追加单位产品所得到的利润值。
期望边际利润：是边际利润乘以其中的追加产品能被卖出的概率。
边际损失：指由于存有一追加单位产品而卖不出去所造成的损失值。
期望边际损失：是边际损失乘以其中的追加产品卖不出去的概率。
[编辑]
- （一）边际分析法的应用
令期望边际利润等于期望边际损失，求出转折概率，根据转折概率对应结果进行决策。
- （二）应用标准正态概率分布进行决策
设有一生产销售问题的风险型决策，如果满足下列两个条件，即：
1、该决策问题的自然状态（市场需求量）为一连续型的随机变量x，其概率密度为f(x)；
2、备选方案d1,d2,...,dm分别表示生产（或存有）数量为1,2,...,m单位的某种产品或商品。
那么，该风险型决策取得最大期望利润值的方案dx，其所代表生产（存有）的单位产品数量k（最佳方案）由下式决定：
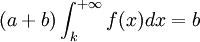
其中：a为边际利润值，即生产并卖出一追加单位产品所获得的利润值；b为边际损失值，即存有一追加单位产品而卖不出去所造成的损失值。
