连线测试

出自 MBA智库百科(https://wiki.mbalib.com/)

连线测试——这个世界没有做不到，只有想不到！

　　连线测试指，在下图的9个点中，要求你用4条直线和3条直线将其一笔连起来，所谓一笔画就是笔不离开纸。主要是测试人的突破框架，发散思维的的能力。

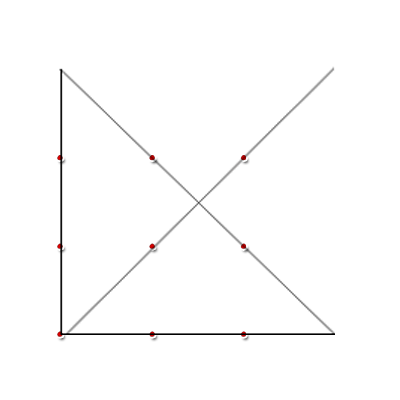
　　1、4条直线连接9个点

　　4条直线将9个点一笔连起来，你第一次做这个游戏的时候你做半天都做不出来，你就在这9个点里面拼命兜圈子，兜圈子，怎么兜都兜不出来，你必须通过9个点给你的限制，用更大的参照系统思考问题，你会发现4条直线经过这9个点就可以把9个点一笔连起来，告诉你你不要说不可能，你必须要把它什么，把它整个的框框给打破。

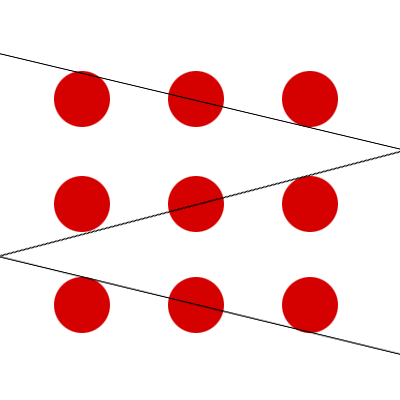
　　2、3条直线连接9个点

　　还是同样9个点，现在要求你用3条直线将它一笔连起来，所谓的一笔连就是笔不要离开是一笔把它连起来，

　　3条直线将9个点一笔连起来，这个游戏起源于日本幼儿园的一道小智力测验题，所以说你不要难过啊。是专门测小朋友智商的，结果发现这个小朋友做出来的速度还是比较快，但是给成人做，就发现见鬼了，成人一般怎么样，一般都做不出来了，其实不是我们懂得比小孩少了，是懂得我们比小孩太多了，所以说这叫什么啊，知识越多越懒惰。

　　我们知道点有没有大小，在数学上很明显点有一个基本假设，点是没有大小的，线是什么，线是没有粗细的，在现实中任何一个点都是有大小的，数学只不过是对现实做了一个假设，而人们在解决任何问题的时候不知不觉都受了这个假设的限制，小孩没学过数学，所以说他没这个假设，

　　连线测试给你最大的启发，这个游戏不是挑战数学，

　　第一，凡是都是可以乱来的，不要有什么规矩，所以说你必须打破一些框框；

　　第二，建议大家不要把刚才这个游戏告诉正在读初中的小朋友，你要告诉他，他以后考试就考不及格了，他就会乱来；

　　第三，凡是我们认为解决不了的并不是真的解决不了，而是我们的限制太多，没有找到方法而已。

　　这个题目的目的不是简单低俗的戏谑，而是各类企业管理，市场营销中常用的一个培训课题中的一个，不管是做广告，管理企业，做业务，各个方面其实都需要我们这种能力，敢于创新，大胆设想，勇于尝试，在激烈的市场竞争中，寻找属于自己的“蓝海战略”。这个世界没有做不到，只要想不到！

　　不是不可能，只是暂时还没有找到方法。这句话就是说，在这个世界上，凡事都可以找到方法予以解决，只不过在日常工作和生活中，我们的大脑已经习惯于受到固有的限制，而不善于创新。

　　1．运用“头脑风暴”法，找到量大质优的方案

　　按照头脑风暴法去工作，将6到8个人组成一个小组，在15分钟之内，对于任何一个难题，相互启发，就可以迅速找到100种以上的解决方案。

　　它的一个理念就是：“量大一定有质优的”，如果仍然没有找到优质的方案，只能说明方案的数量还不够多，这时就要进一步扩大范围。比如分成100个小组，15分钟之后，每个小组会有100种方法，100个组就能达到上万种左右，去掉其中重复的仍会有五六千种，这时，从中就一定能找出最佳的解决方案。

　　2．前提条件是：你必须打破限制

　　任何问题都会有无穷个解决方案，前提条件是你必须打破限制。如果每天都在说“不可能”这三个字，这就限制了我们的思维的发散，并在不知不觉中，将注意力放在为 “不可能”这个结论去寻找理由上。其结果必然是，即使通过努力证明“不可能”这个结论是正确的，对于解决问题本身也没有任何好处。

　　因此，我们应该把口头禅“不可能”这三个字，改成“不是不可能”，只是暂时还没有找到方法。从而打破固有的思维限制，将注意力放在寻找方法上。

• 快乐基金