费马平方和定理

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

费马平方和定理(Fermat's Square and Theorem)

什么是费马平方和定理

　　费马平方和定理是指由法国数学家费马在1640年提出的一个猜想，但他没有提出有力的数学证明，1747年，瑞士数学家莱昂哈德•欧拉提出证明后成为定理。

　　费马平方和定理的表述是：奇质数能表示为两个平方数之和的充分必要条件是该素数被4除余1。

[编辑]

费马平方和定理的证明

　　欧拉在1747年证明了费马平方和定理，当年他四十岁。他在当年5月6日寄给哥德巴赫一封信，讲述这个定理的证明。该证明分五步，且用到了无穷递降法；由于信中没有把第五步讲清楚，因此1749年他再次寄给哥德巴赫一封信，详细讲述第五步的证明。

　　第一步、“如果两个整数都能表示为两个平方数之和，则它们的积也能表示为两个平方数之和。”

　　第一步的证明见婆罗摩笈多－斐波那契恒等式。

　　第二步、“如果一个能表示为两个平方数之和的整数被另一个能表示为两个平方数之和的素数整除，则它们的商也能表示为两个平方数之和。”

　　假设 $a 2 + b 2$ 能被 $p 2 + q 2$ 整除，且后者为素数。则 $p 2 + q 2$ 能整除

　　 $(p b - a q)(p b + a q) = p 2 b 2 - a 2 q 2 = p 2 (a 2 + b 2) - a 2 (p 2 + q 2).$

　　由于 $p 2 + q 2$ 是素数，因此它能整除两个因子之一。假设它能整除 $p b - a q$ 。由于

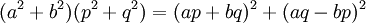
　　 $(a^2+b^2)(p^2+q^2) = (ap+bq)^2 + (aq-bp)^2\,$

　　可推出 $p 2 + q 2$ 能整除 $(a p + b q) 2$ 。于是等式能被 $p 2 + q 2$ 的平方整除。两边除以 $(p 2 + q 2) 2$ 得：

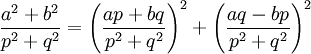
　　 $\frac{a^2+b^2}{p^2+q^2} = \left(\frac{ap+bq}{p^2+q^2}\right)^2 + \left(\frac{aq-bp}{p^2+q^2}\right)^2$

　　因此其商能表示为两个平方数之和。

　　如果 $p 2 + q 2$ 能整除 $p b + a q$ ，则利用等式

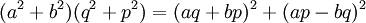
　　 $(a^2+b^2)(q^2+p^2) = (aq+bp)^2 + (ap-bq)^2\,$

　　同样可证。

　　第三步、“如果一个能表示为两个平方数之和的整数被另一个不能表示为两个平方数之和的整数整除，则它们的商也必有一个不能表示为两个平方数之和的因子。”

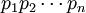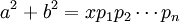　　假设 $x$ 能整除 $a 2 + b 2$ ，且其商的分解式为 $p_1p_2\cdots p_n$ 。则 $a^2+b^2 = x p_1p_2\cdots p_n$ 。如果所有的因子 $p i$ 都能表示为两个平方数之和，则我们可以用 $p 1$ 、 $p 2$ 、等等去除 $a 2 + b 2$ ，并使用第二步的结论，可得每一个商都能表示为两个平方数之和。除到只剩 $x$ 的时候，可得 $x$ 也能表示为两个平方数之和，矛盾。因此，如果 $x$ 不能表示为两个平方数之和，则至少有一个素数 $p i$ 也不能表示为两个平方数之和。

　　第四步、“如果 $a$ 和 $b$ 互素，则 $a 2 + b 2$ 的所有因子都能表示为两个平方数之和。”

　　这一步用到了无穷递降法。设 $x$ 是 $a 2 + b 2$ 的一个因子。可记

　　 $a = mx \pm c,\qquad b = nx \pm d$

　　其中 $c$ 和 $d$ 的绝对值最多不超过 $x$ 的一半。可得：

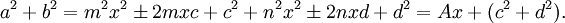
　　 $a^2 + b^2 = m^2x^2\pm 2mxc + c^2 + n^2x^2 \pm 2nxd + d^2 = Ax + (c^2+d^2).$

　　因此， $c 2 + d 2$ 一定能被 $x$ 整除，设 $c 2 + d 2 = y x$ 。如果 $c$ 和 $d$ 不互素，则它们的最大公约数与 $x$ 互质（否则它与 $x$ 的最大公约数就能整除 $a$ 和 $b$ ，与我们假设它们互素矛盾）。因此它们的最大公约数的平方能整除 $y$ （因为它能整除 $c 2 + d 2$ ），于是我们得到 $e 2 + f 2 = z x$ ，其中 $e$ 和 $f$ 互素，且 $z$ 不超过 $x$ 的一半，这是因为

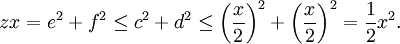
　　 $zx = e^2 + f^2 \leq c^2+d^2 \leq \left(\frac{x}{2}\right)^2 + \left(\frac{x}{2}\right)^2 = \frac{1}{2}x^2.$

　　如果 $c$ 和 $d$ 互素，则我们可直接使用 $c$ 和 $d$ ，不必转换成 $e$ 和 $f$ 。

　　如果 $x$ 不能表示为两个平方数之和，则根据第三步的结论，可知必有一个 $z$ 的因子不能表示为两个平方数之和；设它为 $w$ 。于是我们从 $x$ 推出了一个更小的整数 $w$ ，都不能表示为两个平方数之和，但都能被一个能表示为两个平方数之和的整数整除。由于这个无穷递降是不可能的，因此 $x$ 一定能表示为两个平方数之和。

　　第五步、“任何形为 $4 n + 1$ 的素数都能表示为两个平方数之和。”

　　如果 $p = 4 n + 1$ ，则根据费马小定理可得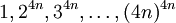 $1, 2^{4n}, 3^{4n},\dots, (4n)^{4n}$ 被 $p$ 除都余1。因此它们的差 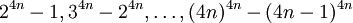$2^{4n} -1, 3^{4n} -2^{4n},\dots,(4n)^{4n} - (4n-1)^{4n}$ 都能被 $p$ 整除。这些差可分解为

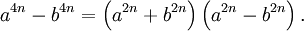
　　 $a^{4n} - b^{4n} = \left(a^{2n}+b^{2n}\right)\left(a^{2n} - b^{2n}\right).$

　　由于 $p$ 是素数，它一定能整除这两个因子之一〔以下称它们为“和因子”和“差因子”〕。如果它能整除任何一个“和因子”，则根据第四步的结论可得 $p$ 能表示为两个平方数之和〔由于 $a$ 和 $b$ 仅相差 $1$ ，它们必然互素〕。而如果它能整除所有的 $4 n - 1$ 个“差因子”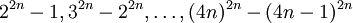 $2^{2n} - 1, 3^{2n} - 2^{2n},\dots,(4n)^{2n} - (4n-1)^{2n}$ ，则它也能整除 $4 n - 2$ 个一阶差、 $4 n - 3$ 个二阶差，依此类推。由于数列 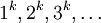$1^k, 2^k, 3^k,\dots$ 的第 $k$ 阶差都等于 $k!$ ，于是第 $2 n$ 阶差都等于 $(2 n)!$ ，显然它不能被 $p$ 整除。因此， $p$ 不能整除所有的“差因子”，得证 $p$ 能表示为两个平方数之和。