矩法估计

出自 MBA智库百科(https://wiki.mbalib.com/)

　　对于随机变量来说，矩是其最广泛，最常用的数字特征，母体ξ的各阶矩一般与ξ的分布中所含的未知参数有关，有的甚至就等于未知参数。由辛钦大数定律知，简单随机子样的子样原点矩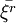依概率收敛到相应的母体原点矩Eξ^r,r = 1,2,Λ。这就启发我们想到用子样矩替换母体矩（今后称之为替换原则），进而找出未知参数的估计，基于这种思想求估计量的方法称为矩法。用矩法求得的估计称为矩法估计，简称矩估计。它是由英国统计学家皮尔逊Pearson于1894年提出的。

　　由辛钦大数定律知：

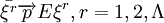
　　即对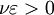，有

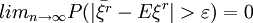
　　或

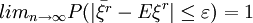
　　设母体ξ的概率函数为f(x,θ₁,Λ,θ_k),其中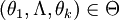是k个未知参数，ξ₁,Λ,ξ_n是取自这一母体的一个子样。设ξ的k阶矩v_k = Eξ^k存在，则v_j,j < k都存在，并且是θ₁,Λ,θ_k的函数v_j(θ₁,Λ,θ_k)，又子样ξ₁,Λ,θ_k的j阶矩为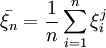。我们设

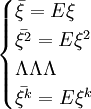　　　　　　(1)

　　这样我们就得到含k个未知参数θ₁,Λ,θ_k的k个方程，解由这k个方程联列所构成的方程组就可以得到theta₁,Λ,θ_k的一组解：

　　　　　　(2)

　　用(2)中的解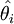来估计参数θ_i 就是矩法估计。

　　一般我们考察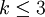的情形。

　　在数理统计学中，我们一般用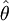表示θ的估计量。

　　下面我们举一个与实际问题有关的多参数的矩法估计问题。

　　例:已知大学生英语四级考试成绩ξ~N(μ,σ²)，均值μ,方差σ²均未知，ξ₁,Λ,ξ_n为取自母体ξ的一个子样，(x₁,Λ,x_n)是子样的一组观测值,求μ与σ²的矩法估计。

　　解：注意到有两个未知参数，由矩法估计知需两个方程，按照(1)式得方程组

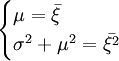
　　解这一方程组得μ与σ的矩法估计量

　　从而μ与σ²的矩法估计值分别为。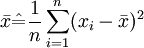

　　分析：注意到我们这里求出μ与σ²的矩法估计并未用到母体ξ的分布。这样对μ,σ²作出了估计，也就对整个母体分布作出了推断，进而对大学生英语四级考试成绩ξ相关的其它数字特征如标准分、标准差、偏态系数等作出了估计。

　　矩法估计原理简单、使用方便，使用时可以不知母体的分布，而且具有一定的优良性质（如矩估计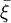为Eξ的一致最小方差无偏估计），因此在实际问题，特别是在教育统计问题中被广泛使用。

　　但在寻找参数的矩法估计量时，对母体原点矩不存在的分布如柯西分布等不能用，另一方面它只涉及母体的一些数字特征，并未用到母体的分布，因此矩法估计量实际上只集中了母体的部分信息，这样它在体现母体分布特征上往往性质较差，只有在样本容量n较大时，才能保障它的优良性,因而理论上讲，矩法估计是以大样本为应用对象的。