矩法估計

出自 MBA智库百科(https://wiki.mbalib.com/)

　　對於隨機變數來說，矩是其最廣泛，最常用的數字特征，母體ξ的各階矩一般與ξ的分佈中所含的未知參數有關，有的甚至就等於未知參數。由辛欽大數定律知，簡單隨機子樣的子樣原點矩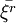依概率收斂到相應的母體原點矩Eξ^r,r = 1,2,Λ。這就啟發我們想到用子樣矩替換母體矩（今後稱之為替換原則），進而找出未知參數的估計，基於這種思想求估計量的方法稱為矩法。用矩法求得的估計稱為矩法估計，簡稱矩估計。它是由英國統計學家皮爾遜Pearson於1894年提出的。

　　由辛欽大數定律知：

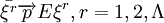
　　即對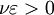，有

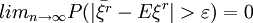
　　或

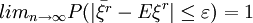
　　設母體ξ的概率函數為f(x,θ₁,Λ,θ_k),其中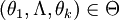是k個未知參數，ξ₁,Λ,ξ_n是取自這一母體的一個子樣。設ξ的k階矩v_k = Eξ^k存在，則v_j,j < k都存在，並且是θ₁,Λ,θ_k的函數v_j(θ₁,Λ,θ_k)，又子樣ξ₁,Λ,θ_k的j階矩為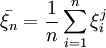。我們設

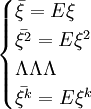　　　　　　(1)

　　這樣我們就得到含k個未知參數θ₁,Λ,θ_k的k個方程，解由這k個方程聯列所構成的方程組就可以得到theta₁,Λ,θ_k的一組解：

　　　　　　(2)

　　用(2)中的解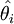來估計參數θ_i 就是矩法估計。

　　一般我們考察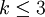的情形。

　　在數理統計學中，我們一般用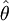表示θ的估計量。

　　下麵我們舉一個與實際問題有關的多參數的矩法估計問題。

　　例:已知大學生英語四級考試成績ξ~N(μ,σ²)，均值μ,方差σ²均未知，ξ₁,Λ,ξ_n為取自母體ξ的一個子樣，(x₁,Λ,x_n)是子樣的一組觀測值,求μ與σ²的矩法估計。

　　解：註意到有兩個未知參數，由矩法估計知需兩個方程，按照(1)式得方程組

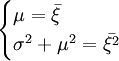
　　解這一方程組得μ與σ的矩法估計量

　　從而μ與σ²的矩法估計值分別為。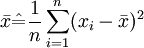

　　分析：註意到我們這裡求出μ與σ²的矩法估計並未用到母體ξ的分佈。這樣對μ,σ²作出了估計，也就對整個母體分佈作出了推斷，進而對大學生英語四級考試成績ξ相關的其它數字特征如標準分、標準差、偏態繫數等作出了估計。

　　矩法估計原理簡單、使用方便，使用時可以不知母體的分佈，而且具有一定的優良性質（如矩估計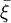為Eξ的一致最小方差無偏估計），因此在實際問題，特別是在教育統計問題中被廣泛使用。

　　但在尋找參數的矩法估計量時，對母體原點矩不存在的分佈如柯西分佈等不能用，另一方面它只涉及母體的一些數字特征，並未用到母體的分佈，因此矩法估計量實際上只集中了母體的部分信息，這樣它在體現母體分佈特征上往往性質較差，只有在樣本容量n較大時，才能保障它的優良性,因而理論上講，矩法估計是以大樣本為應用對象的。