直言推理

出自 MBA智库百科(https://wiki.mbalib.com/)

直言推理（Categorical reasoning）

　　直言推理指的是：关于直言命题的推理^[1]。

　　其中，直言命题也叫性质判断，是断定对象具有或者不具有某种性质的简单命题。例如，“所有金属都是导体”这个判断，认为“金属”这种对象具有“导电”性质，就属于直言命题。

　　无论是哪个领域，无论是做什么工作，每个人都要懂点推理，因为只要涉及到思考、分析，都离不开推理。

　　所谓推理是指，由若干已知判断（前提）获得新判断（结论）思维过程。例如，中，乘警刘瑞国破案就有运用到推理。

　　前提：正常母亲，不会用凉水兑奶粉，喂养新生婴儿。这个女乘客却这么做了。结论：这个女乘客，并不是新生婴儿的亲生母亲。

　　这个推理并不能保证必然成立，因此刘瑞国在如是假设基础上去寻求更多证据。例如，除旁敲侧击外，还通过与女乘客丈夫电话对质等，最终证实假设。

　　在这个过程中，进行合情合理推理是刘瑞国成功破案关键。推理价值，可见一斑。

　　直言推理的的四个部分

　　掌握直言推理，首先要理解直言命题。标准直言命题一般由4个部分组成，分别是：量项、主项、联项和谓项。

　　我们来结合“所有金属都是导体”这个直言命题来识别。

　　其中，量项指的是“所有”、“没有”、“有”等量词，表达数量、范围关系。例如，这个直言命题中，“所有”就是量项。

　　主项指的是命题中对象，通常用大写字母“S”表示。例如，这个直言命题中，“金属”就是主项。

　　谓项指的是命题中对象性质，通常用大写字母“P”表示。例如，这个直言命题中，“导体”就是谓项。

　　联项指的是联结主项和谓项动词，分成肯定和否定两类。例如，这个直言命题中，“是”就是联项。

　　描述直言命题有两个维度，一个是质，一个是量。

　　质是指，直言命题表达的是肯定还是否定关系。不管是全部肯定还是部分肯定，质都是肯定的；不管是全部否定还是部分否定，质都是否定的。

　　量是指，直言命题中量词是全称还是特称。如果是全部，就称为全称；如果是部分，就称为称特。特别的，如果只有一个，称为单称，作为全称特例，合并在全称中。

　　把质和量两个维度结合起来，就可以给直言命题进行分类。用拉丁文单词单缀A、I、E、O简写，具体包括4种：

　　全称肯定直言命题，形式是“所有S都是P”，记为SAP，简称A。例如，所有胎生动物都是哺乳动物。

　　特称肯定直言命题，形式是“有些S是P”，记为SIP，简称I。例如，有的哺乳动物是卵生。

　　全称否定直言命题，形式是“所有S都不是P”，记为SEP，简称E。例如，所有冷血动物都不是恒温动物。

　　特称否定直言命题，形式是“有些S不是P”，记为SOP，简称O。例如，有的哺乳动物不是胎生。

　　日常语言表达时，未必完全按直言命题标准形式表达。在逻辑思考时，为避免推理出错，可以将非标准表达改成标准表达。

　　例如，“低碳技术都绿色”可改成“所有低碳技术都是绿色技术”；类似的，“每只雄鹿都有角” 可改成“所有雄鹿都是有角动物”；“只有知识分子能成为科学家” 可改成“所有能成为科学家的都是知识分子”；“玫瑰不都是红色的”可以改成“有的玫瑰不是红花”。

　　识别概念关系。

　　不管是哪一种直言命题，在判断其真假时，关键就是主项S与谓项P之间关系。

　　例如，“所有金属都是导体”这个直言命题是真是假、是对是错，就在于主项“金属”和谓项“导体”这两个概念是什么关系。

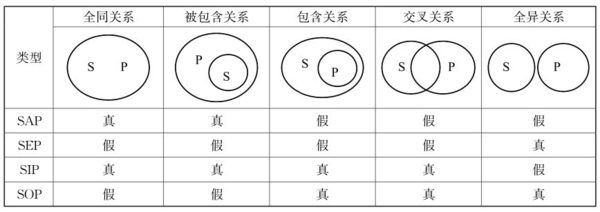
　　如上图解所示，通过维恩图不难发现，主项S与谓项P共存在5种关系，分别是：全同关系、被包含关系、包含关系、交叉关系和全异关系。

　　这容易理解，我们可以用全同关系来做个分析。主项S与谓项P全同，意思就是，S=P，两个集合元素一模一样。

　　那么，SAP判断，“所有S都是P”，自然为真；相反，SEP判断，“所有S都不是P”，自然为假；SIP判断，“有些S是P”，也为真；相反，SOP判断，“有些S不是P”，自然为假。

　　类似的，其它4种关系，借助维恩图，我们也可以快速判断是真是假。

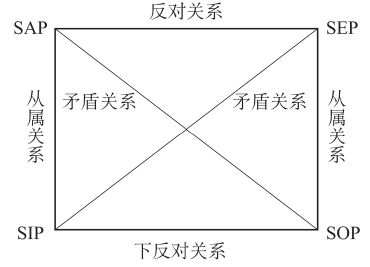
　　从上述判断过程，我们不难发现，4种判断之间真假关系有对应关系。如下图解在逻辑学中称为“对当方阵”，显示出它们之间真假对应关系，包括4种，分别是：矛盾关系、反对关系、下反对关系以及从属关系。

　　其中，矛盾关系是不能同真或者同假。例如，SAP判断和SOP判断，不能同真或者同假。原因不难理解，SAP判断“所有S都是P”，与SOP判断“有些S不是P”，不能同时成立。

　　从属关系又称差等关系，包括4个部分：①如果全称判断真，则特称判断真；②如果特称判断假，则全称判断假；③如果全称判断假，则特称判断真假不定；④如果特称判断真，则全称判断真假不定。

　　前两个部分容易理解，后两个部分我们可以结合具体案例理解。例如，“所有哺乳动物都是卵生”为假，则“有的哺乳动物是卵生”真假不定；“有的哺乳动物卵生”为真，则“所有哺乳动物都是卵生”真假不定。

　　反对关系是指SAP和SEP两个判断不能同真、可以同假关系。包括两个部分：①如果其中一个是真，可以推知另一个为假。例如，“所有被子植物都是种子植物”为真，则“所有被子植物都不是种子植物”为假。②如果一个为假，那么另一个真假不定。例如，“所有哺乳动物都是卵生”为假，那么“所有哺乳动物都不是卵生”真假不定。

　　下反对关系是指SIP和SOP两个判断不能同假、可以同真关系。包括两个部分：①如果其中一个为假，可以断定另一个为真。例如，“有的孢子植物是种子植物”为假，那么 “有的孢子植物不是种子植物”为真。②如果其中一个为真，那么另一个真假不定。例如，“有的哺乳动物不是胎生”为真，那么“有的哺乳动物是胎生” 真假不定。

　　以上均只是示例，我们有兴趣可以自己举例，熟悉四种直言命题之间真假关系。在实际推理时，可以借助维恩图，既直观快速，又能避免出错。

　　理解直言命题，识别概念关系后，涉及到直言命题时，我们就有条件合情合理推理，并准确判断真假。

　　比如说，运用对当方阵直接推理。

　　根据对当方阵，可以得出如下结论；

　　①如果A真，那么，E假，I真，O假；如果A假，那么，O真，E、I真假不定；

　　②如果E真，那么，A假，I假，O真；如果E假，那么，I真，A、O真假不定；

　　③如果I真，那么，E假，A、O真假不定；如果I假，那么，A假、E真、O真；

　　④如果O真，那么，A假，E、I真假不定；如果O假，那么，A真，E假、I真。

　　例如，已知“有些树叶有叶绿素”为真，可以进行如下推理：

　　“有些树叶没有叶绿素”（不确定）；“所有树叶都有叶绿素”（不确定）；“所有树叶都没有叶绿素”（假）；“柳树叶没有叶绿素”（不确定）；“杨树叶有叶绿素”（不确定）。

　　相反，如果违背对当方阵真假对应关系，就可能产生推理谬误。

　　例如，有一个判断是：“中国运动员有人获得法国网球公开赛（简称法网）冠军，所以，有的中国运动员不能获得法网冠军。”

　　这个判断前提是“有的中国运动员获得法网冠军”。“有的”表示存在，可以是全部，可以是有些，也可以只是一个。因此，推理不出“有的中国运动员不能获得法网冠军”。

　　直言推理虽然不复杂，但如果没有熟练掌握，就可能被人愚弄。

　　我们来看一个故事。1870年在《镀金时代》小说发表后，美国作家马克·吐温在一次酒会上答记者问时说：“美国国会中有些议员是狗娘养的。”这句话见报后，华盛顿议员们大为愤怒，纷纷要求马克·吐温道歉或者予以澄清，否则将以法律手段对付。

　　过了几天，《纽约时报》上刊出马克·吐温致联邦议员“道歉启事”。全文如下：日前鄙人在酒席上发言，说“美国国会中有些议员是狗娘养的。”事后有人向我兴师问罪。我考虑再三，觉得此话不妥，而且也不符合事实。故特登报声明，把我的话修改如下：“美国国会中有些议员不是狗娘养的。”

　　在这个案例中，“美国国会中有些议员是狗娘养的”是I判断；“美国国会中有些议员不是狗娘养的”是O判断。I判断的否定命题并不是O判断，马克·吐温故意违反逻辑规则来讽刺国会议员，表面上按要求“纠正”自己表达，加上“不”字，但实质并没有改变。