理发师悖论
出自 MBA智库百科(https://wiki.mbalib.com/)
理发师悖论（Barber paradox）
目录 |
理发师悖论是罗素悖论的通俗举例，是由伯特兰·罗素在1901年提出的。罗素悖论的出现是由于朴素集合论对于元素的不加限制的定义。由于当时集合论已成为数学理论的基础，这一悖论的出现直接导致了第三次数学危机，也引发了众多的数学家对这一问题的补救，最终形成了现在的公理化集合论。同时，罗素悖论的出现促使数学家认识到将数学基础公理化的必要性。
一个城市里唯一的理发师立下了以下的规定:只帮那些自己不理发的人理发。
现在问一个问题:理发师应该为自己理发吗?
你会发现理发师处于两难,因为:
- 如果理发师不给自己理发，他需要遵守规则，帮自己理发.
- 如果理发师是自己理发的，他需要遵守规则，不给自己理发
换用集合语言：
可以把集合分为两类，凡不以自身为元素的集合称为第一类集合；凡以自身作为元素的集合称为第二类集合。显然每个集合或为第一类集合或为第二类集合。设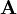
为第一类集合的全体组成的集合。
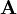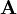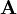- 如果是第一类集合，由集合的定义知:应该是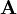的元素，这表明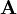是第二类集合
- 如果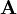是第二类集合，那么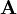是它自身的元素
二者皆导出矛盾，而整个讨论逻辑上是没有问题的。问题只能出现在集合的定义上。
设对于一类集合，
都满足条件
但
一切这类集合构成新集合
，
那么是否有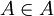
？如果认为
则A应该不是自身集合的元素，即
，如果
就应是本集合的元素，即，所以矛盾。
由于罗素悖论的出现所引发的第三次数学危机，公理化集合论势在必行。 德国数理逻辑学家策梅洛（Zermelo，1871年-1953年）应用自己的公理系统，使得集合在[[公理] ]的限制下不会太大，从而避免了罗素悖论。经过改进，这一系统形成了现在被称为ZF系统的公理集合论体系。这个体系至今没有发现悖论。
罗素悖论、理发师悖论和异己词悖论的关系[1]
按我们通常对集合的理解，我们可以把集合分成两种，一种是属于自身的，即自己是自己的元素，另一种是不属于自身的。设S是由所有不自身的集合组成的集合，那么S是否属于它自己？若S属于S，依S的定义，S中的元素都不应该属于自己；而若S不属于S，则按照S的定义，S应该是所有不属于自己的集合构成的集合，那么S又属于S。即不论假定S属于自己还是不属于自己，都将导致矛盾。
理发师悖论与罗素悖论是等价的。因为，如果把每个人看成一个集合，这个集合的元素被定义成这个人刮脸的对象。那么，理发师宣称，他的元素，都是村里不属于自身的那些集合，并且村里所有不属于自身的集合都属于他。那么他是否属于他自己？这样就由理发师悖论得到了罗素悖论。反过来的变换也是成立的。
异己词悖论：在语言中，有些形容词可以描述自身，有些形容词则不可以描述自身。例如形容词 “short”（短的）和“English”（英国的）可以修饰自身，因为short只有五个字母，English本身也是英语单词。而“long”（长的）和“French”（法国的）则不能修饰自身。又如“polysyllabic”（多音节的）这个词是多音节的，但“monosyllabic”（单音节的）这个词却不是单音节的。看来可以这么说，一个词或者可以用于自己，或者不可以。我们称那些能描述自身的词为同己的（autological），称那些不能描述自身的词为异己的（heterological）。现在让我们来考虑异己的（heterological）这个词，它是同己的还是异己的呢？如果它是同己的，则依同己的定义，它能描述自身，所以它是异己的。如果它是异己的，由于它能描写自身，所以应该是同己的。这样一来，每一个关于这个词的假设都会导致矛盾。
我们按照理发师悖论和罗素悖论关系那样思考，我们把一个词与一个集合关联，这个集合是由这个词所能修饰的词构成的，那么异己的（heterological）这个词就恰恰对应了罗素悖论中“所有不自身的集合组成的集合”。这么说来，异己词悖论也等价于罗素悖论。如果用符号来表示异己词这一概念，则更加明显：X是异己的，如果X并非X。这和罗素悖论中的“X属于S，如果X不属于X”何其相似！实际上，它们的逻辑结构相同。
但是，我至今没有看到哪本书上叙述过它们的这种关系，所有介绍这几个悖论的书都只是明确承认前两个悖论是等价的，而异己词悖论经常被单独讨论。甚至有些书上竟然把异己词悖论说成是一种“语义学悖论”，而把罗素悖论说成是纯逻辑悖论。这样的分法有什么根据呢？难道异己词悖论中涉及词语本身的语义，就说它是语义学的吗？按照《数学，确定性的丧失》的说法，语义学悖论“涉及到一个词的真实性和可定义性或模糊应用等概念，相应地采用这些概念的严格定义能解决上述悖论。”这提醒我们，有些词义本身是模糊不清的，比如说，长度为多少的词可以用long来修饰？没有什么标准。但是，如果把所有英语形容词的词义严格地界定起来，那么异己词悖论就真正等价于罗素悖论了。所以，悖论本身并没有因为概念的严格定义而得到解决。
评论(共41条)
身份不可能重叠。从严格意义上来讲，如果理发师自己不是老板，那么必然有制度规定他上班的时候，只能是服务者而不能是被服务者，如果服务自己的话，就会被开除。即便冒着被惩罚，服务自己，那么他也不是在工作，可以视为旷工，那么他就是被服务者，逻辑上没有矛盾。如果理发师自己是老板，那么他可以决定自己何时上班，何时休息。他服务于自己的时候，由他自己决定是上班还是休息。但是无论是上班还是休息，他都只能有一种身份。一种身份的前提下，就不会出现逻辑的矛盾。
我觉得这似乎是一种游戏，这个游戏带人走进思维缭乱的难以抉择状态。以命题为题的话，如果要遵守规则分析是否符合其规则化。这将会让你脑溢化而让思维出卖自己。
命题是说，理发师只为不给自己理发的人理发（此句可以导出：不为给自己理发的人理发），而没有说给所有不给自己理发的人理发，所以，他可以不给自己理发。
真不愧为哲人的高论! 但如果按这样一直推论下去的话,是不是可以这样理解:法官只是给除他(她)之外任何人定罪的法官,而与他(她)自己犯不犯法无关? 警察可以尽管抓坏人,而自己永远不用担心有其他警察抓他(她)?即便是违法? 教师无论怎样教育学生他(她)都是在行使他(她)的教育别人的权利,而无论是正确与错误的教学方式? 而孩子永远只有言听计从,而丝毫没有权利辩解真正的是非对错?
身份不可能重叠。从严格意义上来讲，如果理发师自己不是老板，那么必然有制度规定他上班的时候，只能是服务者而不能是被服务者，如果服务自己的话，就会被开除。即便冒着被惩罚，服务自己，那么他也不是在工作，可以视为旷工，那么他就是被服务者，逻辑上没有矛盾。如果理发师自己是老板，那么他可以决定自己何时上班，何时休息。他服务于自己的时候，由他自己决定是上班还是休息。但是无论是上班还是休息，他都只能有一种身份。一种身份的前提下，就不会出现逻辑的矛盾。
认同
针对条目内容如有需要表达自己观点的地方，请在条目下方的评论框中进行评论。
如条目内容有错误或者需要完善的时候，编辑时请先预览，达到自己预期后再保存。谢谢合作！
住要是元素在定义的条件下拥有了可变性,而相悖点就来源这可变性 定义的东西可变，那不是定义不明么，却还是在以他定义，这能没问题么？
理发师本身有两种身份：服务者和被服务者。成为服务者身份时不帮自己理发；当成为被服务者时应该自己理发。人类本身就存在多种身份，该命题是哲学家故意抛开这个条件而设计的。任何命题在条件不充分时都会是悖论。
对
理发师本身有两种身份：服务者和被服务者。成为服务者身份时不帮自己理发；当成为被服务者时应该自己理发。人类本身就存在多种身份，该命题是哲学家故意抛开这个条件而设计的。任何命题在条件不充分时都会是悖论。
嗯嗯 不同的角色扮演下就会有不同的立场。如果一定要忽视这一点的话那只能是悖论
呵呵。这个理发师只能选择不理发，或者请别人给自己理发。因为他一旦给自己理发就属于犯规，在此逻辑上属于不可完成任务，就如人不可能完全由自己徒手举起自己一样，属于逻辑死角。A属于不给自己理发，B属于给自己理发的人，那么理发师超脱于两者之外，当他属于A时他可以通过完成任务转变成B但是又违反了获得任务的原则。
理发师本身有两种身份：服务者和被服务者。成为服务者身份时不帮自己理发；当成为被服务者时应该自己理发。人类本身就存在多种身份，该命题是哲学家故意抛开这个条件而设计的。任何命题在条件不充分时都会是悖论。
GOOD
我觉得这似乎是一种游戏，这个游戏带人走进思维缭乱的难以抉择状态。以命题为题的话，如果要遵守规则分析是否符合其规则化。这将会让你脑溢化而让思维出卖自己。
思维出卖自己。有点意思。
叫理发师帮自己理个头给我看看
理发师基本都是自己给自己理发
身份不可能重叠。从严格意义上来讲，如果理发师自己不是老板，那么必然有制度规定他上班的时候，只能是服务者而不能是被服务者，如果服务自己的话，就会被开除。即便冒着被惩罚，服务自己，那么他也不是在工作，可以视为旷工，那么他就是被服务者，逻辑上没有矛盾。如果理发师自己是老板，那么他可以决定自己何时上班，何时休息。他服务于自己的时候，由他自己决定是上班还是休息。但是无论是上班还是休息，他都只能有一种身份。一种身份的前提下，就不会出现逻辑的矛盾。
厉害
身份不可能重叠。从严格意义上来讲，如果理发师自己不是老板，那么必然有制度规定他上班的时候，只能是服务者而不能是被服务者，如果服务自己的话，就会被开除。即便冒着被惩罚，服务自己，那么他也不是在工作，可以视为旷工，那么他就是被服务者，逻辑上没有矛盾。如果理发师自己是老板，那么他可以决定自己何时上班，何时休息。他服务于自己的时候，由他自己决定是上班还是休息。但是无论是上班还是休息，他都只能有一种身份。一种身份的前提下，就不会出现逻辑的矛盾。
这个假设很不错
GOOD
我觉得楼上说得很对，但是要补充的是。被服务者应该是一个不给自己理发的人；服务者就可以看做一个给自己理发的人。如果是双重身份就可以看做服务者为被服务者理发，这样是不是就不矛盾了
我觉得这个问题很简单，理发师可以帮自己理发，只能理一次发，没理发前理发师没帮自己理过发，理发后他就是一个帮过自己理发的人，之后就不可以帮自己理发
如果理发师自己不理发，他需要遵守规则，帮自己理发.这话讲得特别好！
然后他帮自己理发，就违反了规则因为他不能给自己理发的人理发
我觉得楼上说得很对，但是要补充的是。被服务者应该是一个不给自己理发的人；服务者就可以看做一个给自己理发的人。如果是双重身份就可以看做服务者为被服务者理发，这样是不是就不矛盾了
这样只是把理发师分成了两个人而已
我觉得楼上说得很对，但是要补充的是。被服务者应该是一个不给自己理发的人；服务者就可以看做一个给自己理发的人。如果是双重身份就可以看做服务者为被服务者理发，这样是不是就不矛盾了
无非是用花言巧语掩盖了自己是自己这一事实
我觉得这个问题很简单，理发师可以帮自己理发，只能理一次发，没理发前理发师没帮自己理过发，理发后他就是一个帮过自己理发的人，之后就不可以帮自己理发
自己不理发和自己没理过发的区别，这个悖论讨论的就是正在理发时的矛盾性
理发师本身有两种身份：服务者和被服务者。成为服务者身份时不帮自己理发；当成为被服务者时应该自己理发。人类本身就存在多种身份，该命题是哲学家故意抛开这个条件而设计的。任何命题在条件不充分时都会是悖论。