模糊多属性决策
出自 MBA智库百科(https://wiki.mbalib.com/)
模糊多属性决策（Fuzzy MADM，简称FMADM）
目录 |
什么是模糊多属性决策 [1]
由于决策问题中属性水平和目标水平的表示方式可以是定量的，即数字的，也可以是定性的，即语言的其数据结构可以是精确的，即刚性的，也可以是不精确的，即柔性的。模糊多属性决策，是一种认为在决策时，决策空间是离散的，一个对事物的评价选择问题。
与经典多属性决策相似,模糊多属性决策的基本模型可以描述为给定一个方案集在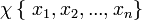 
，和相应于每个方案的属性集合
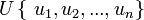，以及说明每种属性相对重要程度的权集
。
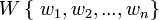其中关于属性指标和权值的大小的表示方式可以是数字的，也可以是语言的涉及的数据结构可以是精确的，也可以是不精确的，而所有语言的或不精确的属性指标，权值的大小和数据结构等都被相应地表示成决策空间中的模糊子集或模糊数。
其模糊指标值矩阵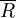
可以写为:
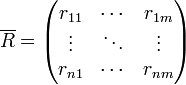
模糊多属性决策的演变情形[1]
经典多属性决策的主要概念和基本算法在模糊环境中的改进和演变情形主要如下：
- （1）从实数权值和实数指标值到模糊权值和模糊指标值
在模糊多属性决策中，属性的权值和指标值可全部或部分地表示为模糊集或模糊数。
- （2）从实数运算到模糊数的运算
模糊多属性决策中涉及的模糊数运算类型主要有算术运算的加、减、乘、除，代数运算的乘方、开方、指数、对数，和逻辑运算的极大、极小等。
- （3）从正理想解和负理想解到模糊极大集和模糊极小集
正理想解和负理想解在经典多属性决策中是两个重要的参照基准。对于收益类指标来说，正理想解由各项指标的最大值组成，负理想解由极小值组成而成本类指标的情况反之。由于实数空间中的大小概念是明明白白的，正理想解和负理想解的确定十分容易。但在模糊空间中，大小的判断随可能性水平的变化而变化，致使正理想解和负理想解的确定变得十分复杂和困难，至今也没有形成统一的认识。
比较常见而自然的做法是，先通过模糊指标值与模糊权值的合成运算。求出代表每一方案所具价值的模糊效用集，并定义诸模糊效用集中的模糊极大集或模糊极小集作为决策的参照基准。然后，通过比较各模糊效用集与参照基准之间的距离，选出其中与模糊极大集的距离最小者或与模糊极小集的距离最大者作为决策的最佳方案。
- （4）从欧几里得距离到海明距离
由于经典多属性决策中的正理想解和负理想解在模糊多属性决策中被模糊极大集和模糊极小集所代替，方案与参照基准之间的距离测度也从原欧几里得距离变为海明距离。
模糊多属性决策的应用 [2]
垃圾卫生填埋场场址选择具有模糊性，主要表现在两个方面：一是对垃圾卫生填埋场选址的影响因素的评估往往是不确切的。二是对于影响因素的权重估计，也很难给出一个精确的值。基于这种情况，可将垃圾卫生填埋场选址视为一个决策问题，通过采用模糊多属性决策方法来加以解决。
垃圾卫生填埋场选址的因素很多，除了法规方面的因素外，主要影响因素还有交通运输条件建场条件水文地质条件，气象条件地形条件5个方面。
对于影响因素，通常可以用“很好”、“好”、“一般”、“差”、“很差”5个模糊词语进行评价，称为评价等级。影响因素的评价等级是5个模糊词语，为反映其模糊性，采用模糊数来表示评价等级。
例如某铁路路段垃圾卫生填埋处置场有4个备选场址，通过专家评分确定了各场址影响因素的评价等级及其权重，见附表。
表 专家评定表
交通运输条件 建场条件 水文地质条件 气象条件 土壤条件 场址1 很好 一般 好 好 一般 场址2 差 很好 差 好 一般 场址3 很好 好 一般 一般 好 场址4 很好 一般 很好 好 一般
常用的模糊数有梯形模糊数﹑三角模糊数等，其中三角模糊数的形式为N=(l ， m ，r)。根据三角模糊数的表示形式和意义，影响因素的评价等级的模糊数分别为:“很好”为(0.8 ，0.9，1)，“好”为(0.6 ，0.7 ，0.8)，“一般”为(0.4 ，0.5 ，0.6)，“差”为(0.2，0.3 ，0.4)，“很差”为(0 ，0.1 ，0.2)。
