时间序列分解法

出自 MBA智库百科(https://wiki.mbalib.com/)

时间序列分解法（Time-series Decomposition）

　　时间序列分解法是数年来一直非常有用的方法,这种方法包括谱分析、时间序列分析和傅立叶级数分析等。

　　时间序列y可以表示为以上四个因素的函数，即：

　　Y_t = f(T_t,S_t,C_t,I_t)

　　时间序列分解的方法有很多，较常用的模型有加法模型和乘法模型。

　　加法模型为： Y_t = T_t + S_t + C_t + I_t

　　乘法模型为：

　　（1）运用移动平均法剔除长期趋势和周期变化，得到序列TC。然后再用按月（季）平均法求出季节指数S。

　　（2）做散点图，选择适合的曲线模型拟合序列的长期趋势，得到长期趋势T。

　　（3）计算周期因素C。用序列TC除以T即可得到周期变动因素C。

　　（4）将时间序列的T、S、C分解出来后，剩余的即为不规则变动，即：

　　时间序列一般包括四类因素，长期趋势因素、季节变动因素、循环变动因素和不规则变动因素。四种因素的组合形式一般有以下几类, 其中记Xt为时间序列的全变动；Tt为长期趋势；St为季节变动；Ct为循环变动；It为不规则变动，它总是存在着的。

　　1） 乘法模式，其中，

　　a) X_t与T_t有相同的量纲，S_t为季节指数，C_t为循环指数，两者皆为比例数；

　　b)

　　c) I_t是独立随机变量序列，服从正态分布。

　　2）加法模式 X_t = T_t + S_t + C_t + I_t

　　这种形式要求满足条件：

　　a) X_t，T_t，S_t，C_t，I_t均有相同的量纲；

　　b) ,k为季节性周期长度；

　　c) I_t是独立随机变量序列，服从正态分布。

　　3) 混合模式

　　a) X_t与T_t，C_t，I_t有相同的量纲，St是季节指数，为比例数；

　　b)

　　c) I_t是独立随机变量序列，服从正态分布。

　　时间序列分解法试图从时间序列中区分出这四种潜在的因素，特别是长期趋势因素(T)、季节变动因素(S)和循环变动因素(C)。显然，并非每一个预测对象中都存在着T、S、C这三种趋势，可能是其中的一种或两种。一个具体的时间序列究竟由哪几类变动组合，采取哪种组合形式，应根据所掌握的资料、时间序列及研究目的来确定。

　　分解法的基础是容易理解而且直观的。不过最重要的是它为预测和检验提供了独特和非常有用的资料。我们用一个例题来说明各个因素分解的步骤。

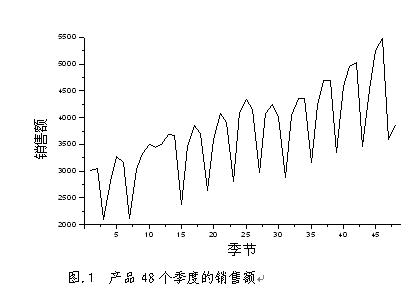
　　设有某产品十二年（91年－02年）的季度销售额数据。见表4.3中的第二列，共有48个数据。如果将这些数据画在图上（图.1），可以看出有明显的长期趋势和季节变动。利用分解法，假设这48个数据可表示为。这里X_t是这些原始数据，通过分析原始数据X来确定T、C、S（剩下的为I）。

　　1．移动平均数

　　把最初的四个数据（表示91年4个季度的值）相加求平均值得到(X₁ + X₂ + X₃ + X₄) / 4 = 2741.334。这个数是没有季节性的，而且随机性因素也很小甚至没有。因为随机性围绕中间值波动，将四个数相加，正负波动在一定程度上相互抵消了，所以可认为其中已无随机性。同样将第二个至第五个数据相加平均， 也不包含季节性，而且其随机性因素也很小。如此我们可得到45个数据。它们不包含季节性，而且随机性因素很小甚至没有。也就是说它们只包括长期趋势和循环变动两部分（T×C）。这45个数据组成的序列我们称之为移动平均数序列，用MA来表示，MA＝T×C。

　　2．季节性

　　由于　　（1）

　　因此将观察值除以移动平均数得到的比率值就只包含季节性和随机性，从而这些比率包括了确定季节性因素所需要的信息。如果某个比率的值>100，意味着实际值X比移动平均数（T×C）要大。由于X中包含季节性和随机性，因而当比率值大于100时，就意味着这个季度的季节性和随机性高于平均数。反之，如果比率小于100，则表示季节性和随机性低于平均数。

　　表.2 某产品48个季度的销售数据及数据分解

季度	观察值Xt	移动平均值T×C	S×I比率％	长期趋势T	循环变动C％
1	3017.60	——	——	2774.81	——
2	3043.54	——	——	2813.77	——
3	2094.35	2741.334	76.339	2852.73	96.10
4	2809.84	2805.632	100.150	2891.69	97.02
5	3274.80	2835.569	115.490	2930.65	96.76
6	3163.28	2840.558	111.361	2969.61	95.65
7	2114.31	2894.240	73.052	3008.57	96.20
8	3024.57	2907.411	104.030	3047.53	95.40
9	3327.48	2989.961	111.288	3086.49	96.87
10	3493.48	3071.367	113.744	3125.45	98.27
11	3439.93	3187.921	76.537	3164.41	100.74
12	3490.79	3277.322	106.514	3203.37	102.31
13	3685.08	3319.258	111.021	3242.33	102.37
14	3661.23	3303.883	110.816	3281.29	100.69
15	2378.43	3296.073	72.159	3320.25	99.27
16	3459.55	3337.209	103.666	3359.21	99.34
17	3849.63	3347.198	115.010	3398.17	98.50
18	3701.18	3413.185	108.438	3437.13	99.30
19	2642.38	3444.678	76.706	3476.09	99.10
20	3585.52	3501.936	102.387	3515.05	99.63
21	4078.66	3553.405	114.782	3554.01	99.98
22	3907.06	3597.425	108.607	3592.97	100.12
23	2818.46	3723.421	75.695	3631.93	102.52
24	4089.50	3788.657	107.941	3670.89	103.21
25	4339.61	3849.043	112.745	3709.85	103.75
26	4148.60	3874.540	107.101	3748.81	103.35
27	2976.45	3872.325	75.315	3787.77	102.23
28	4084.64	3848.029	106.149	3826.73	100.56
29	4242.42	3810.274	111.342	3865.69	98.57
30	3997.58	3801.414	105.160	3904.65	97.36
31	2881.01	3789.311	76.030	3943.61	96.09
32	4036.23	3818.788	105.694	3982.57	95.89
33	4360.33	3909.526	111.531	4021.53	97.21
34	4360.53	3982.320	109.497	4060.49	98.07
35	3172.18	4029.203	78.730	4099.45	98.29
36	4223.76	4111.740	102.724	4138.41	99.36
37	4690.48	4195.228	111.805	4177.37	100.43
38	4694.48	4237.770	110.777	4216.33	100.51
39	3342.35	4326.237	77.258	4255.29	101.67
40	4577.63	4394.982	104.156	4294.25	102.35
41	4965.46	4477.872	110.889	4333.21	103.34
42	5026.05	4509.818	111.447	4372.17	103.15
43	3470.14	4496.895	77.167	4411.13	101.94
44	4525.94	4570.210	99.031	4450.09	102.70
45	5258.71	4611.094	114.045	4489.05	102.72
46	5489.58	4642.750	111.778	4528.01	102.53
47	3596.76	4481.667	80.255	4566.97	98.13
48	3881.60	——	——	4605.93	——

　　由式（1）可知，如果能将S×I中的随机性部分去掉，则就得到了季节性指数。要做到这一点，只需注意到随机性指的是偶然性、没有一定模式、围绕中间值0上下波动。因此通过平均就能去掉随机性的影响。将表4.3中“S×I比率”这一栏列成表4.6的形式，将各年同一季度的数据放在同一列之中，求相同各季度的平均值，得第一至第四季度的平均数分别为112.72，109.88，76.28，103.86。由于从1991年至2002年各年中相同季度的数值加以平均消除了大部分随机性，因此这四个平均数仅仅代表了季节性。用代数式表示即为

　　 (2)

　　其中中上面的横线表示季节平均。

　　表3 产品销售额的季节性指数

年份	各季度季节指数
	第一季度	第二季度	第三季度	第四季度
1991	—	—	76.40	100.15
1992	115.49	111.36	73.05	104.03
1993	111.29	113.74	76.54	106.51
1994	111.02	110.82	72.16	103.67
1995	115.01	108.44	76.71	102.39
1996	114.78	108.61	75.70	107.94
1997	112.75	107.10	75.32	106.15
1998	111.34	105.16	76.03	105.69
1999	111.53	109.50	78.73	102.72
2000	111.81	110.78	77.26	104.16
2001	110.89	111.45	77.17	99.03
2002	111.84	111.78	80.26	—
平均数	112.72	109.88	76.28	103.86
修正平均数	111.95	109.13	75.76	103.16

　　表3中的四个平均值相加的和为402.74，它不等于400。为了使各季节指数的平均数等于100，必须进行简单的调整。如果400被合计数402.74来除，结果是0.9932。以0.9932乘以各季节的平均数得到111.95，109.13，75.76，103.16等（见表中最后一行）。现在这四个季节指数的和为400，它们的含义就更加清楚了，例如第二季度的109.13就表示第二季度比全年平均数高出9.13％，第三季度的75.76表示第三季度比全年低24.24％。

　　3．长期趋势和循环变动

　　前面介绍的公式MA=T×C表示了一组循环变动—长期趋势数值。在多数情况下这样已能满足要求，但有时仍需要把循环变动和长期趋势分离开来。为了做到这一点，我们只需确定一种能最好的描述数据长期趋势的类型。例如长期趋势可以是线性的、二次的、S曲线或其它。对于本例，如果将数据在图上画出来，可以看出线性的长期趋势是比较合适的：

　　T_t = a + bt　　（.3）

　　t = 1,2,3…48。用最小二乘法可求得模型的最佳拟合参数为：

　　a = 2735.85, b = 38.96

　　因此趋势直线方程为

　　T_t=2735.85+38.96t

　　如图4所示。用此方程即可求得每个季度的趋势值。如第20季度（2000年的第四季度）趋势值为

　　T_{20}=a+bt=3515.05

　　由于MA=T×C，因此

　　MA/T=(T\times C)/T=C　　 (4)

　　应用上式即可求得循环变动值C。如第45季度的循环变动值C_{45}等于表3中的移动平均数除以T_{45}，即

　　如同季节指数，循环指数也采取百分比率。其值大于100的表明该季度经济活动水平高于所有季度的平均值，而小于100的循环指数所表明的情况则刚好相反。

　　循环因子比较复杂，且其变动周期较长，因而在短期预测中可以忽略不计，或将其归入到趋势变化之中（称为趋势—循环因子）。人们更关心的是趋势和季节的识别。

　　至此我们完成了对原始数据Xt的分解工作，其步骤总结如下：

　　1） 用MA=T×C分析长期趋势和循环变动；

　　2） 用分析季节性和随机性；

　　3） 用分析季节性；

　　4） 用趋势外推法中介绍的方法来分析长期趋势；

　　5） 用MA / T = C分析循环变动。

　　总之，分解法提供了分析时间序列各种因素的手段，它使用简单，只需用加法、乘法和除法等简单代数运算即可，而且分解法非常直观，能给企业提供一定时期内的大量信息。

　　用分解法确定了季节指数、趋势值和循环指数之后，就可以根据上面总结的步骤进行预测了。我们对2003年第一季度（第49季度）进行预测。数据的基本关系式为

　　X=T×C×S×I

　　由于随机性无法直接进行预测，进行预测的关系式为：

　　X=T×C×S

　　于是，计算出第49季度的T₄₉,C₄₉,S₄₉值即可求得第49季度的预测值。

　　表3中已得到第一季度的季节指数为111.95，由趋势方程求得

　　最后循环指数通常要根据判断估算出来，或者用某种方法预测得到。这里我们假定通过判断为：C₄₉ = 98，于是

　　同样可以对第50、51季度进行预测。

　　1. 居中移动平均数

　　为了求得移动平均数MA，上面我们是将相邻的4个原始数据相加取平均得到一个数，这样在表4.5的第三列中就少了三个数据。于是产生了这样一个问题：最初的四个数据被平均时，它们的平均数应该置于何处？严格讲应该放在第二季度和第三季度的中间（（1＋4）/2＝2.5，第2.5个季度）。其余数据取平均时也有类似的问题。但实际数据是表示各个季度而不是半个季度的，这里我们只好将平均数放在靠后半个季度的地方。假如对平均数再取平均的话就不会产生这样的问题了，因为如第一季度至第四季度的平均数2741.34是指第2.5季度，而第二季度至第五季度的平均数是指第 3.5季度，则它们的平均数就是指第3个季度（（2.5＋3.5）/2=3）。称如此的平均数为居中移动平均数，于是居中移动平均数比原始数据少四个（首尾各两个）。

　　现在，实际值除以居中移动平均值所得的比率（还是S×I）也可以用来计算季度指数，具体的与上面所述完全一样。这样求得的四个季度的季节指数分别为112.20，109.44，75.37，103.17，其和为400.18，非常接近于400，这是因为移动平均数居中的缘故。

　　2．分解法的改进

　　在上面所叙述的分解法基础上，我们也可作一些改进，如：

　　1） 修正原始数据中工作日或营业日的差额。由于各个月度（或季度）的工作日是不尽相同的，这就会影响到销售额或别的所要预测的变量。因此首先必须对数据进行校正。如对月度数据的校正可通过原始数据乘以30对工作日的比率来进行，即将各月度的原始数据折算到工作日均为30天的统一情况。

　　2） 利用统计方法来淘汰极值（即修改或舍去超出标准差的三倍范围的数值），在分解法实施之前先对数据进行预处理。

　　3） 按上一节求得的季节性指数还可进一步改进，并进行动态的调整，因为实际上季节指数并不一定是一成不变的，它本身亦是一个变化的时间序列。

　　还应注意到用分解法进行预测时，循环因素的确定是最为困难的。如有什么秘诀的话，那就是应具备足够数量的历史数据，以使管理人员了解循环模式是从哪里开始重复的，必要时可用图表方法来帮助确定。由于循环模式可能会发生变化，按照管理人员的判断对循环模式作一些调整无疑是必要的。

　　在前面的两个子节中，我们是以周期为4的季度数据的一个例题来说明分解法的分解步骤和预测程序。对周期为12月度数据、周期为7的日常数据等其它情况，运用分解法的程序完全类似，在此不再举例讨论。

　　分解法能帮助解释历史数据为什么变化，能使管理人员分别预计各局部模式的变化。这些局部模式不仅能用以预测，而且也可用于管理之中，再加上它容易被管理人员所理解，因此分解法在直观上吸引了许多管理人员的注意，从而被大量的用于实际问题的预测。经过成千上万个时间序列的反复检验，分解法被证明其效率和准确性都是较高的。当然这种证明是经验的而非理论的，这也是它的主要缺点。它不能用统计的方法来检验，也不能建立置信区间。实际上，分解法仅适用于那些季节性较强的中期预测、短期预测，当预测目标受外界干扰较大时，其预测能力会明显减弱。

　　时间序列是由一个包括了4个部分的模型组合而成，即T、S、C、R。假定影响时间序列的这四个因素彼此相互作用、非独立，那么我们采用相乘的模型[4,P460]，即Y，=T×C×S×R。该方法包括以下四个步骤：1.用4季度移动平均法确定季节性指数[4,P463]。其基本原理是用移动平均法来度量趋势和周期性组合(TC)。这种做法可以消除季节性和随机变动的影响，即S和R。做法如下：(1)计算时间序列中的4季度移动平均值(TC_1)，例：(500+350+250+400)／4=375。

　　(2)对4季度移动平均值再求其移动平均值的中点值(TC_2)^[2]，例：(375+362.5/2=368.75)。

　　计算真实销售额(3)计算真实销售额(Y_1)与移动平均值(TC_2)的比率，这个比率实际上表示的季节性和随机变动综合作用的部分^[2],即SR=Y/TC。

　　(4)把计算处的比率值按季度排列，例如

　　第一季度的SR值分别是：1.263、1.367、1.467、1.222、1.348；

　　第二季度的SR值分别是：1.037、0.762、0.812、0.853、0.879；

　　第三季度的SR值分别是：0.678、0.640、0.522、0.588、0.700；

　　第四季度的SR值分别是：1.003、1.067、1.206、1.275、1.116。

　　然后后按季度分别计算平均比率以便剔除随机变动(R)的影响，而该平均比率称为季节性因子(S_1)。例：对于第一季度的计算：(1.263+1.367+1.467+1.222+1.348)／5=1.333 4。依次类推计算第二、三、四季度的s1分别得：1.33 4、0.908 6、0.625 6、1.153 4。(5)对季节性因子(S₁)进行调整，调整后的季节性因子(用S₂表示)。

　　例：第一季度的S₂计算：1.333 40-0.005 25=1.328 15，其中0.00525=(1.333 4+0.908 6+0.625 6+1.153 4-4)/5。同样，第二、三、四季度的S₂分别是：0.903 35、0.620 35、1.148 15。上述(1)、(2)、(3)、(4)、(5)的计算结果如下表。

　　2.从原始时间序列中剔除季节性变化影响，即进行非季节性处理^[2]。从附图中观测销售额与时期是否有线性变化趋势。通过观测发现：1994～1995年销售额有下降的趋势，1996-1999年销售额有上升的趋势。但是，前两年下降的趋势不明显，后四年一直是上升趋势。因此，可以近似看作销售额(Y)与时间(t)有线性关系，并依据非季节性数据作线性回归方程：Y₂ = a + b_t其中。

　　将表3中的数据代入上述公式得：Y=149.673+20.882t　　(3)

　　3.将t=25、26、27、28代人第二步求得的回归方程(3)，并乘上相应的季节性因子S₂，则得出2000年每一季度的销售额预测值。即：Y₂5 = 892.149、Y₂6 = 625.665、Y_27=442.612、Y₂8 = 843.1664，在附图上作出上述回归方程(3)的图形。

　　采用时间序列分解法时，必须观察时间t与非季节性数据Y_2的趋势关系。若t与Y₂的趋势变化是近似于线性的，则可用线性回归方程预测;若Y₂对t来说是呈几何级数增长，则宜用指数曲线回归方程;若是其他变化，必须采用相应的其他回归方程。

　　采用线性回归方程来预测，但是由于前两年的数值是下降的，后四年的数值是上升的，因此，使得该回归方程的拟合度不是很好。但是，这种影响程度会随着t的增加而减弱，最终不会影响预测的精确度，因为总趋势是上升的。，采用时间序列分解法预测时，由于前两年的数值有下降的趋势，而拟合的是上升趋势的线性回归方程，因此，用该方法预测短期(1-2年)的销售额不准确，通过附图可以看出。

• 西安电子科技大学.《决策与预测》第4章 确定型时间序列预测方法.

• 时间序列预测法
• 简单时间序列平滑法