无套利机会模型

出自 MBA智库百科(https://wiki.mbalib.com/)

无套利机会模型(Arbitrage-free Model)

　　无套利机会模型是指利用当前的债券市场价格推导出短期利率的未来演变过程，无套利机会模型推导出的结果必须符合当时的利率期限结构。

　　该类模型引入了利率的二项式变动，是在利率波动的约束条件下寻求利率的运行轨迹。Hoand Lee(1986)认为任何期限的利率水准都等于短期期限的利率水准加上或减去某种随机冲击，从而形成一个预期利率树。由于Ho—Lee模型关于各种利率水准发生的相对频率呈正态分布和利率的波动不受利率水准影响的假设不切实际，随后出现了一些修正模型，如OriginalSalomonBrothers模型(布鲁斯，1999)、Black—Derman—Toy模型(Blacketc．，1990)和Black—Karasinski模型(Black and Karasinski，1991)。无套利机会模型主要是基于预期理论建立起来的模型。它们认为债券市场价格是合理的，并将利率期限结构视为既定，故缺乏持续性。

　　无套利机会模型定价的过程是，以观察到的当时的利率期限结构为模型的输入，假设短期利率的随机过程，由零息债券到期时价值依次向前推算，得出每一期的债券价格，同时可以得出债券期权的价格。

　　(1)Ho和Lee模型(1986年)

　　Ho和Lee在1986年的论文中首先提出了期限结构的无套利模型。他们用债券的二叉树图的形式提出了该模型。模型有两个参数：短期利率的标准差和该短期利率风险的市场价格。模型的结构为：

　　dr = θ(t)dt + σdw

　　其中，短期利率的瞬态标准差σ是常数，而θ(t)是为了保证模型与初始期限结构一致而选择的时间的函数。

　　在Ho和Lee模型中，贴现债券和基于贴现债券的欧式期权可以求出解析解。用短期利率表示的t时间的贴现债券价格的表达式是：

　　P(t,T) = A(t,T)e ^{− r(t)(T − t)}

　　其中：

　　Ho和Lee模型的优点是它是可解析处理的马尔科夫模型，它的应用简便而且能精确地符合当前的利率期限结构。模型的缺点是：①在选择标准差时给予使用者的灵活性太小，所有即期和远期利率都具有相同的瞬态标准差σ；②不具有均值回复性，这意味着在某个特定时点上，不论利率多么高或多么低，利率在下一个短时间内移动的平均方向总是一样的。

　　(2)原始的所罗门兄弟模型(1987年)

　　在原始的所罗门兄弟模型(original Saloman brother model)中，新利率等于原有利率乘以一个随机冲击。因此，这个模型是以“乘法”而不是“加法”来处理随机冲击的。这将以对数正态分布取代正态分布，同时克服了Ho—Lee模型中利率可能为负的缺陷。

　　该模型的结构为：

　　dlnr = m(t)dt + σdw

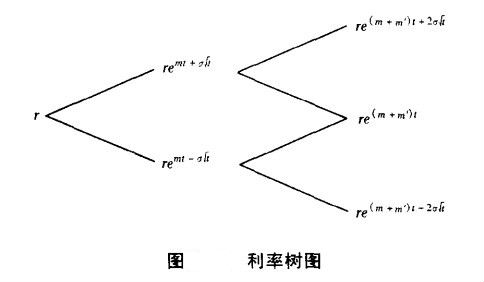
　　其中，m(t)是关于时间t的趋势变量。短期利率的演变过程如图所示。

　　模型中的参数σ称为“比例波动率”，m'是下一时刻的m(t)。短期利率的实际波动率等于比例波动率乘以当时的短期利率，表明短期利率的波动率随利率变化而变化，并不是如Ho-Lee模型中假设为常数。

　　原始的所罗门兄弟模型的优点是：①用对数分布取代正态分布，克服了Ho—Lee模型中利率可能为负的缺陷；②短期利率的波动率与利率成正比，并不是常数。许多业内人士认为假设比例波动率为常数优于假设短期利率的波动率为常数(如：Ho—Lee模型)。该模型的缺点是没有反映现实生活中的利率均值回复现象。

　　(3)Black—Derman—Toy模型(1990年)

　　相对于所罗门模型来说，Black—Derman—Toy模型的最主要的优点是可以反映利率期限结构的实际波动情况。这是因为它假设短期利率波动率将随时间而变动，而利率的趋势变量m将受到利率水准的影响。

　　许多研究者认为，当利率水准偏高时，它的趋势变量(drift，指m的数字而言)相对较小，甚至为负值；当利率水准偏低时，趋势变量相对较大。换言之，他们相信利率具有均值回归性。

　　Black—Derman—Toy模型具有均值回复的性质，但这个性质是通过波动率的期限结构而显现的。换言之，趋势变量受到利率水准的影响程度，完全取决于短期利率的演变过程。这种方法有一个缺点，即以不精确的方式呈现均值回复的性质，主要依靠估计短期利率的未来波动率来近似实现均值回复。这种不精确性可能对模型的定价功能产生不利的影响。所以，模型或许应该在不受波动率过程的影响下，单独考虑回归均数的性质。

　　模型的结构：

　　其中，θ'是下一个时间段短期利率r的瞬时标准差。这个模型与其他无套利机会模型一样，它对于零息债券所定的价格必须等于市场价格。可是，在波动率的期限结构方面，这个模型所提供的结果可以符合实际的情况，为了达到这个目的，Black—Derman—Toy模型允许短期利率的波动率随着时间而变动，所以这种波动率又称为“区域性波动率”。然而，随着时间而变动的区域性波动率会引起一些问题，因为利率可能呈现非结合性的树状图。树状图无法结合，解决的办法是，让上行与下行状况的未来发展各具不同的趋势变量。

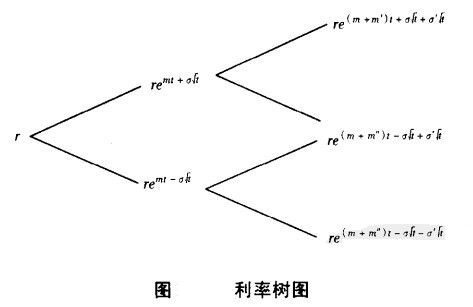
　　假定m'代表由上行状态发展的趋势变量，m''代表由下行状态发展的趋势变量，则短期利率的树状图将如图所示。

　　如果“上行-下行状况”与“下行-上行状况”的利率相等，树状图便会结合：因而设定：

　　这相当于

　　即趋势变量完全由短期利率的波动率来决定，从而实现均值回复。

　　Black—Derman—Toy模型的优点是：①利率波动率随时间而变动，优于假设为常数；②具有均值回复特性：缺点是：趋势变量完全由短期利率的波动率来决定，这种方式也是不精确的，模型应该在不受波动率过程的影响下，单独考虑均值回复的性质。

　　(4)Black—Karasinski模型(1990年)

　　Black—Karasinski模型是以明显的方式来处理均值回复，它假设短期利率有一个中央倾向，并设定短期利率回归中央倾向的速度。这个模型可以从数种不同的角度来建立。可以设定均值回复的某些合理参数值，或设定均值回复的速度为某一常数，然后调整模型中的其他参数，让利率期限结构与波动率的期限结构能够相互协调。或者，也可以设定区域性波动率的参数值，然后凋整其他参数值，让利率期限结构与波动率的期限结构能够相互协调、第三种方法是原作者所建议的方法，它以市场的某组数值来套入模型，其中以差价上限选择权曲线(differential cap curve)(差价上限选择权是根据某名义金额，支付短期利率与履约利率的差价(如果这项差价为正值))尤其实用。将差价上限选择权的价格套入模型中，并倒推模型的参数值，这是希望模型在确定其他或然性合约的价格时，便能够反映市场的实际情况。

　　模型的结构：

　　dlnr = Φ(t)[lnμ(t) − lnr]dt + σ(t)dw

　　其中：μ(t)是目标利率(target rate)，Φ(t)表示均值回复，σ(t)表示区域波动率，即lnr的波动率。

　　Black—Karasinski模型的优点：①允许独立设定均值回复的行为；②由于它足对数正态分布的模型，利率水准不可能为负，利率的波动率与利率的水准成比例。缺点足利率的树状图仍呈现非结合性的树状图，均值回复的行为将受到波动率结构的影响。

　　(5)Hull和White模型(1990年)

　　Hull和White在1990年、1993年的论文中提出了自己的模型，他们的模型主要是对Vasicek和CIR模型进行了扩展，在短期利率模型中加入了依赖时间t的参数θ(t)。他们认为考虑时间因素是合理的，因为经济的景气循环、人们对将来货币政策及其他宏观经济变量的预期都与时间有关。

　　他们建议的Vasicek模型的扩展形式是：

　　dr = [θ(t) + a(t)(b − r)]dt + σ(t)dw

　　很显然，当a=0、θ(t)常数时，该模型就是Ho—Lee模型。

　　利用ITO定理，得出债券价格的微分方程，求解微分方程，可以求得债券价格的解析式：

　　P(t,T) = A(t,T)e ^{− B(t,T)t(t)}

　　其中：

　　他们建议的CIR模型的扩展形式是：

　　同样，也给出了相应的零息债券价格表达式。

　　Hull和White模型的贡献主要是对Vasicek和CIR模型进行了扩展，考虑了时间因素对利率的影响。

　　(6)HJM模型(Heath，Jarrow and Moaon)(1992年)

　　Heath、Jarrow和Morton等人建立了远期利率的期限结构模型。在此之前的期限结构模型都是从假设债券价格或即期利率服从某种随机过程人手的。Heath、Jarrow和Moron首先指出：在漂移率(drift)和瞬态远期利率的标准差之间存在着某种联系。

　　模型结构：

　　其中f(t,T)表示在t时刻观测到的T时刻到期合约的瞬态远期利率，表示利率过去值、当前值和t时刻债券价格的矢量，α(·)和σ(·)分别表示远期利率的瞬时均值和瞬时标准差。

　　Heath，Jarrow和Morton通过无套利定价原理导出了瞬态远期利率的漂移率与波动率之间的关系，即：

　　这样，只要通过估计瞬态远期利率的波动率，就可得到远期利率的漂移率：也就是说，不必估计漂移率，就可以求出债券的价格。

　　通过远期利率模型可以求得短期利率的随机模型，这种短期利率的随机模型与其他一些模型直接假设短期利率服从布朗运动不同，它是非马尔科夫过程，可以用蒙特卡罗模拟方法来处理期限结构的一般非马尔科夫过程，但耗时过久。

　　HJM模型的优点主要有：①与其他无套利模型一样，符合当前的期限结构；②债券及其期权的价格由利率的波动率来决定，不必估计利率的漂移率；③不用假设投资偏好。缺点是短期利率树图不重合，一般用蒙特卡罗方法来模拟，计算起来要慢些。

　　(1)取得模型需要的资料不同。就有关利率风险的市场价格来说，无套利机会模型需要即期利率期限结构的资料，这些利率资料相对容易取得。均衡模型却需要以某种方法宋衡量投资者承担利率风险所要求的报酬，这方面的资料远较即期利率难以取得，通常必须以统计方法来分析过去的价格与利率走势。所以，就取得模型所需要的资料来说，无套利模型显然具有优势。

　　(2)对资料缺陷的敏感程度不同。无套利机会模型将即期利率期限结构模型视为合理，实际上，某些市场报价并不合理，这可能是因为计算卜的错误、市场流动性或其他特殊因素所造成的。无套利机会模型会将这类的资料缺陷纳入定价模型中，可是，均衡模型会剔除这类有问题的价格，这也正是该类模型的特色。

　　(3)模型的持续性不同。每当运用的时候，无套利机会模型需要假设趋势变量、波动率与利率均值回复的行为。可是，在两个不同的运用日期，模型所设定的数据没有持续性。举例来说，在某一天，模型所采用的趋势变量将涵盖未来的20年，但使用者知道，明天必须运用今天的利率期限结构的资料，重新设定趋势变量。总之，无套利机会模型缺乏持续性、相反，均衡模型是根据历史资料或某些坚定的信念来设定参数，所以模型的参数不会每

• 一般均衡理论