逻辑思维
出自 MBA智库百科(https://wiki.mbalib.com/)
逻辑思维(Logical Thinking),也称抽象思维(Abstract thinking)
目录 |
逻辑思维是人们在认识过程中借助于概念、判断、推理反映现实的过程。它与形象思维不同,是用科学的抽象概念、范畴揭示事物的本质,表达认识现实的结果。逻辑思维是一种确定的,而不是模棱两可的;前后一贯的,而不是自相矛盾的;有条理、有根据的思维;在逻辑思维中,要用到概念、判断、推理等思维形式和比较、分析、综合、抽象、概括等方法,而掌握和运用这些思维形式和方法的程度,也就是逻辑思维的能力。
逻辑思维是分析性的,按部就班。做逻辑思维时,每一步必须准确无误,否则无法得出正确的结论。我们所说的逻辑思维主要指遵循传统形式逻辑规则的思维方式。常称它为“抽象思维”或“闭上眼睛的思维”
在逻辑思维中,是使用否定来堵死某些途径。比喻说,逻辑思维是在深挖一个洞,它就是为了把一个洞挖得更深的工具。
逻辑思维是人脑的一种理性活动,思维主体把感性认识阶段获得的对于事物认识的信息材料抽象成概念,运用概念进行判断,并按一定逻辑关系进行推理,从而产生新的认识。逻辑思维具有规范、严密、确定和可重复的特点。
- 逻辑的来源与含义[1]
在汉语中“逻辑”是一个外来词,它是通过音译的方法从西文引入汉语的。在拉丁文、英文和德文中它分别是“logica”、“logic”和“logik”。而西文中的这些词都来源于古希腊文的“λσγoζ”,它有语言、说明、比例、尺度等多种涵义。亚里士多德曾使用这个词来表示事物的定义或公式等。到了公元1世纪,学者们就用这个词来表示一门与论证辩论等许多问题相关的学问,而亚里士多德的三段论被看作这一学问的核心内容。
“逻辑”是一个外来词,这并不意味在中国思想发展史中就没有研究相关理论的学问。春秋战国时期的著名学者公孙策的“白马说”,墨子的“墨经”等都反映出在我国古代学者们在这方面的研究成果,它们构成了中国古代逻辑思想研究的精髓。在中国哲学史上,这些理论研究的内容称作“名学”或“辩学”。
汉字作为一种表意文字,“名学”“辩学”这些词在表意上是含混的,如果顾名思义,这些词显然不能准确表达出逻辑学作为一门科学理论的研究内容。因此近代学者们沿用西方的做法,引入音译词“逻辑”,对于逻辑学的涵义则用定义进行规定。
尽管是一个外来词,“逻辑”在我们日常运用中仍然表现为一个多义词。有时它被用来表示一种理论或观点,如“这简直是强盗逻辑”。有时它可被用来表示规律性的东西,如“它的出现符合事物发展的逻辑”。人们有时还用它来表示对一些特殊逻辑规则和方法的运用,如“他的文章很有逻辑”,“这篇文章逻辑性强”。
然而,上述说法都没有正确说明究竟什么是作为科学理论的逻辑,也没有准确描述逻辑学研究的对象以及逻辑学的理论特征。而这些都是学习逻辑学首先需要了解的问题。
“逻辑”的古希腊词源[1]:
“逻辑”源自于“逻各斯”(logos,其复数形式是logoi),其主要含义有:
①一般的规律、原理和规则。
②命题,说明,解释,论证等。
③理性,推理,推理能力,与经验相对的抽象理论,与直觉相对的有条理的推理。
④尺度,关系,比例,比率等。
“逻各斯”的基本词义是言辞、理性、秩序、规律,其中核心含义又是“秩序”和“规律”,其他含义都是由此派生出来的。例如,“有秩序的”、“合乎规律的”就是合乎“理性”的;“推理”就是按照“规律”进行有“秩序”的、有条理的思维。西方各门科学的词尾“学”字(-logy),均起源于“逻各斯”这个词,“逻辑”一词更是从它引申出来的。
“逻辑”的现代汉语词义为:
①客观事物的规律,例如:“历史的逻辑决定了人类社会将一直向前发展。”
②某种理论、观点,例如:“只许官家放火,不许百姓点灯,这是哪一家的逻辑!”
③思维的规律、规则,例如:“某个说法不合逻辑”。
④逻辑学或逻辑知识,例如“大学生应该上逻辑课”。
1、概念的特征:内涵和外延。
2、判断的特征:一是判断必须对事物有所断定;二是判断总有真假。
3、推理的特征:演绎推理的逻辑特征是:如果前提真,那么结论一定真,是必然性推理;非演绎推理的逻辑特征是:虽然前提是真的,但不能保证结论是真的,是或然性推理。
1、有助于我们正确认识客观事物。
2、可以使我们通过揭露逻辑错误来发现和纠正谬误。
3、能帮助我们更好地去学习知识。
4、有助于我们准确地表达思想。
逻辑思维在创新中的作用:
1、逻辑思维在创新中的积极作用
- 发现问题;
- 直接创新;
- 筛选设想;
- 评价成果;
- 推广应用;
- 总结提高。
2、逻辑思维在创新中的局限性
- 常规性;
- 严密性;
- 稳定性。
1、分析与综合
分析是在思维中把对象分解为各个部分或因素,分别加以考察的逻辑方法。综合是在思维中把对象的各个部分或因素结合成为一个统一体加以考察的逻辑方法。
2、分类与比较
根据事物的共同性与差异性就可以把事物分类,具有相同属性的事物归入一类。具有不同属性的事物归入不同的类。比较就是比较两个或两类事物的共同点和差异点。通过比较就能更好地认识事物的本质。
分类是比较的后继过程,重要的是分类标准的选择,选择的好还可导致重要规律的发现。
3、归纳与演绎
归纳是从个别性的前提推出一般性的结论,前提与结论之间的联系是或然性的。演绎是从一般性的前提推出个别性的结论,前提与结论之间的联系是必然性的。
4、抽象与概括
抽象就是运用思维的力量,从对象中抽取它本质的属性,抛开其他非本质的东西。概括是在思维中从单独对象的属性推广到这一类事物的全体的思维方法。
抽象与概括和分析与综合一样,也是相互联系不可分割的。
1、逻辑思维渗透于一切创造过程中
逻辑思维的过程形式与创新、创造过程密切相关,一切创造活动都是以逻辑思维为基础的,运用逻辑思维对创造成果条理化、系统化、理论化。
2、逻辑思维与创新思维的一般区别
1)思维形式的区别。逻辑思维的表现形式,是从概念出发,通过分析、比较、判断、推理等 形式而得出合乎逻辑的结论。创新思维则不同,它一般没有固定的程序,其思维方式大多都是直观、联想和灵感等。
2)思维方法的区别。逻辑思维的方法,主要是逻辑中的比较和分类、分析和综合、抽象和 概括、归纳和演绎,而创新思维的方法,主要是一种猜测、想象和顿悟。
3)思维方向的区别。逻辑思维一般是单向的思维,总是从概念到判断再到推理,最后得出 结论。创新思维的思维方向则是很多的,结果也是多样性的。
4)思维基础的区别。逻辑思维是建立在现成的知识和经验基础上的,离开已有的知识和经验,逻辑思维便无法进行。创新思维则是从猜测、想象出发,没有固定的思维方式,虽然也需要知识和经验作为基础,但不完全依赖知识和经验。
5)思维结果的区别。逻辑思维严格按照逻辑进行,思维的结果是合理的,但可能没有创新 性。创新思维活动既然不是按照常规的逻辑进行,其结果往往不合常理,但其中却有新颖性的结果。
3、逻辑思维与创新思维在创新活动中的关系:衔接关系;互补关系;转化关系。
逻辑思维的基本规律[2]
同一律的内容是:在同一个思维过程中,反映同一个对象的思想是确定的,必须始终保持同一个含义,不能偸换它的含义。
同一律要求思维必须具有确定性。
就命题而言,同一律要求,一个命题如果代表的是某个事件,它就必须始终代表这一事件。如果这一事件是事实,那么该命题就是真的;如果命题代表的事件不是事实那么命题就是假的。因此同一律认为,一个命题必须有确定的真值,如果是真的那么它就是真的,如果是假的那么它就是假的。这一要求我们可以用“p→p”表示。
就词项而言,同一律要求,一个词项如果指称某个对象,它就必须始终指称这个对象。就是说词项a就是a,它具有确定的外延和内涵,并始终保持同一的外延和内涵,即保持自身同一。这一要求可用公式“a=a”表示。
违反同一律的要求,就会产生逻辑错误。这样的逻辑错误主要有两个方面:
- 1、混淆词项,又叫作混淆概念的逻辑错误
语词具有多义性,一个语词一般来说同含义、对象之间并无一一对应关系。同一语词往往可以表达多种不同的含义,指称多种不同的对象,这就是语词的多义性与歧义性,它导致了语词相同但表达的词项不同的现象,使混淆词项、混淆概念等逻辑错误的产生成为可能。
我们把那些在同一思维过程中,不加说明、定义地用同一个语词项表达不同的含义,指称不同的对象所犯的逻辑错误,称为混淆词项、混淆概念。以同一字眼或同一语词表达不同的词项,或者说赋予同一语词以不同的含义是这种逻辑错误的典型表现。
如在《韩非子》中有这样一则故事:郑县有一位姓卜的,他常常在外鬼混。一天他的裤子弄出了一个洞。他买了新布,回家让妻子为他作一条新的裤子。妻子问他如何做,他说“照原样”。于是他妻子把裤子照原来的样式做好后,照样在裤子原来的地方剪了一个洞。这当然是一个笑话。但从逻辑的角度来说,他的妻子是有意或无意地违反同一律。“原样”在丈夫的那里指的是原来样式的、尺寸,绝不是有破洞的原样。
在使用语词表达词项、指称对象时,如果是无意地违反了同一律的要求,所犯的错误就称为“混淆词项”或者“混淆概念”。如果是故意违反同一律要求以达到某种目的,就称为“偷换词项”或者“偷换概念”。两者的区别只在违反同一律的动机上而并不在形式上。
- 2、混淆论题的逻辑错误
在没有语境限制的情况下,同一语句可以陈述不同的内容,即它表达的涵义有可能是不相同的,这就是语句的歧义性。这就使“混淆论题”逻辑错误的产生成为可能。我们把那些在同一思维过程中用一个似是而非的论题来代替原来的论题的现象称作“混淆论题”的逻辑错误。
例如,鲁迅在其杂文里曾经谈论到一位不懂逻辑的排长。他写道:“这排长的天真,…他以为不抵抗将军下台,‘不抵抗’就一定跟着下台了。这是不懂逻辑:将军是一个人,而不抵抗是一种主义,人可以下台,主义却可以仍旧留在台上的。”(《鲁迅全集》第5卷第116页)鲁迅提到的这位天真的排长所以错误,就在于他把“不抵抗将军下台”和“不抵抗主义下台”混为一谈,违反了同一律的要求犯了“混淆论题”的逻辑错误。
不自觉地或者无意地以一个似是而非的论题来代替原论题的,称为混淆论题。但如果别有所图而故意违反同一律要求混淆论题的称为“偷换论题”的逻辑错误。
同一律从形式上说,只是关于逻辑形式表述思维时应当遵守的规律。只有遵守同一律的要求,才能使思维在表述上具有确定性。因此可以说,遵守同一律是人们正确认识事物的必要条件,它要求我们在表述思维的同一过程中,任何一个词项都要前后一致地保持含义即内涵的相同,并且使指称对象即外延也相同,否则,我们在词项的理解上就要发生混乱;任何一个命题都要前后一致地保持意义即内容上的相同和在真假断定上的相同, 否则,我们在命题的理解上就要发生混乱。 词项或命题在理解上的混乱,都将导致思维本身的混乱,从而不可能去正确地进行思维以真实地认识客观世界。不能准确无误地去表达、交流思想,也就不可能在思想交流的过程中及时地发现、揭露和反驳谬论或诡辩。
说遵守同一律是正确地表达思维的必要条件,是说违反了同一律,对思维的表达必定是错误的,但遵守了同一律,对思维的表达也未必一定是正确的。例如,在“教育是有阶级性的,教育是社会现象,所以,社会现象是有阶级性的”这一推论过程中所表现出来的思维活动,检查其使用的词项和命题,一般来说都被认为是遵守了同一律的,但这个推理活动仍然是错误的。因此,我们应当恰如其分地而不是夸大地把握同一律的认识作用。
说遵守同一律是正确地表达思维的必要条件,还强调着同一律只是在人们运用逻辑形式的过程中起作用的规律,它作用的对象仅仅是人们所使用的逻辑形式,是运用逻辑形式的规律,这显然有别于我们常说的客观世界本身的规律。因此不能把人们对事物的不同观点、不同理解,以及运用词项表示发展并丰富起来的概念、运用命题对同一事物从不同的角度所陈述的不同观点等等都看成是对同一律要求的违反。这也就是说,不能把同一律和形而上学的世界观一概而论。同一律既不否定客观世界本身的运动性、发展性、丰富多彩性,也不排斥人们在认识客观世界是所持有的辩证唯物主义的观点。
矛盾律也称为不矛盾律。它的内容是:在同一思维过程中,关于同一对象的思想必须始终保持一致,不能自相矛盾。
矛盾律要求思维必须具有一致性。
就命题而言,由于在同一时间同一关系上一个事件不可能即存在又不存在,因此我们不可能对同一命题作出不同的断定,不能既断定它真,又断定它假。由此矛盾律要求:两个互相否定的命题不可能都真,必有一个是假的。矛盾律的这一要求可用公式“?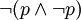 ”表示.。例如,我们不能既断定“这个证人的所有话都是真的”,同时又断定“这个证人的有些话不是真的”。
”表示.。例如,我们不能既断定“这个证人的所有话都是真的”,同时又断定“这个证人的有些话不是真的”。
就词项而言,同一律的要求可用公式“a ≠ a ”表示。即要求不能用两个相互的否定的词项指称同一个对象,并且同一个词项不能包含自相矛盾的东西。例如,“方的圆”、“可以溶化一切的溶液”等都是违反矛盾律的。
逻辑矛盾是在同一思维过程中对同一对象做出互相否定的表述时所产生的逻辑错误。如上所述,互相否定的表述形式可分为相互矛盾的命题和相互反对的命题,因此违反矛盾律的逻辑错误尽管我们都把它称为“自相矛盾”,但在应用时则应分为两种情况去处理。
首先,是在同一思维过程中对一对矛盾命题的表述同时予以肯定或者否定而产生的逻辑错误。矛盾命题在真或者假上总是不相容的,我们既不能同时断定它们都真,也不能同时断定它们都假。不妨以命题形式p→q和~(p→q)为例,它们的真值表分别是
- p→q ~(p→q)
- TT T F TT T
- TF F T TF F
- FT T F FT T
- FT F F FT F
显然,在对命题形式赋值的同一过程中, p→q和~(p→q)的真值在任何条件下都是既不同真也不同假的。它表明,只要我们肯定p→q就要否定~(p→q),而否定p→q就要肯定~(p→q),反之亦然。在传统逻辑中,把违反矛盾律的要求,在同一思维过程中同时肯定或否定一对矛盾关系的命题产生的错误称为“自相矛盾”,我国先哲韩非子在《韩非子?难一》中所讲的一个寓言故事,最为生动地反映了自相矛盾的这种错误。该故事描写了的一个既卖矛又卖盾的楚国人,他吹嘘自己的矛是世界上最为锋利的,以至于“任何东西都能被它扎透”;继而,他又炫耀自己的盾,是世界上最为坚固的,是“没有任何东西能扎透它的”。旁边有好事者问他,“若以你的矛扎你的盾,其结果又如何呢?”这个卖矛又卖盾的楚国人只好张口结舌,无以为答了。其所以不能对答,就在于他在宣传自己的矛与盾的过程中所陈述的两个命题“任何东西都能被它扎透”和“没有任何东西能扎透它的”,它们构成了一对逻辑矛盾,因而犯了“自相矛盾”的逻辑错误。
我们在说话、写文章等等过程中,如果不注意思想的前后一贯性,就可能出现逻辑矛盾。例如,有人说:“实践是检验真理的唯一标准,但马克思列宁主义也是检验真理的标准”这肯定是自相矛盾的。因为既然说前者是“唯一的”,那么其他的标准又从何而来呢?又如“大家相互作了自我批评”,显然,是“自我批评”就不是“相互”的,而是“相互”的也决不是“自我批评”,尽管这里只出现了一个命题,但却是一个自相矛盾的命题。
其次,违反矛盾律的错误,是在同一思维过程中对一对表述反对关系的命题同时予以肯定而产生的逻辑错误。把在同一思维过程中对一对表述为反对关系的命题同时予以肯定依旧归结为“自相矛盾”,这是符合矛盾律的要求的,因为具有反对关系的一对命题本质上是相互否定的,在同一思维过程中对它们都肯定显然是错误的。但是,矛盾律对具有矛盾关系和反对关系的命题在如何制约上是有区别的。对矛盾关系的命题来说,矛盾律肯定其一真一假,当其中一个命题为真时,另一个命题则必然是假的,反之亦然;而对具有反对关系的命题来说,矛盾律尽管可以由其中一命题的真肯定另一命题的假,但反之却不成立,因为具有反对关系的命题是可以同假的。我们以命题形式p∧q与p∧~q的真值表来比较说明。
- p∧q p∧~q
- TT T TF F T
- TF F TT T F
- FF T FF F T
- FF F FF T F
从上述真值表的第二、五两列可以看出,虽然p∧q取真时p∧~q必然取假, p∧~q取真时p∧q必然为假,但当p∧q取假时, p∧~q是可以同时为假的,反之也一样。这表明,当矛盾律作用的对象是具有反对关系的一对命题时,我们不能由其中的一个命题假去推断另一个命题的真。
遵守矛盾律的要求,同样是思维得以正确表达的必要条件。换言之,只有遵守了矛盾律的要求,思维在由逻辑形式的表述过程中才能首尾一贯,前后一致,表达准确。而违犯矛盾律的要求,在思维的表达上必然是相互矛盾的,因此,最终导致思维也是混乱的。例如,如果我们在同一时间去既肯定命题“我们班的同学现都在军训”,又肯定命题“我们班第一小组的同学现正在上心理学课”,这就违反了矛盾律的要求,在命题的表述上是自相矛盾的。但如果我们同时肯定“我们班有的同学是党员”和“我们班有的同学是非党员”,尽管此时的谓项是一对具有矛盾关系的词项,但两个命题既无脑袋关系又无反对关系,因此并不违犯矛盾律的要求。矛盾律也是我们进行反驳的一个重要理论依据,人们在反驳一个假命题时,常常是间接地去证明这个假命题的矛盾命题或反对命题为真,从而根据矛盾律去说明原命题的假。而在确立某个命题的真时,也可以去证明该命题的矛盾命题的假, 从而根据矛盾律去说明原命题的真,但此时应当注意的是,所涉及的两命题现在必须是矛盾关系而不是反对关系。
排中律的内容是:在同一思维过程中,关于同一事物的两个相互矛盾的思想不可能都是假的,必有一个为真。因此,对于两个互相矛盾的命题,我们必须作出明确的选择.必须肯定其中之一为真。排中律的这一要求可用公式“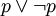 ”表示。
”表示。
要注意,根据排中律的内容,排中律适用于“两个相互矛盾的思想”,这与矛盾律适用“两个相互否定的思想”有所不同。排中律所适用的一般来说是具有矛盾关系的命题。但也有一些特殊情况。如具有下反对关系的两个命题,由于它们不可能都假,因此也必须断定其中一个为真。
例如命题“这个报告提供的数据有些是真实的”与“该报告提供的数据有些不是真实的”,这两个命题不可能都是假的,必有一个为真。我们否定其中的一个真,就必须肯定另一个为真。而具有形式“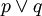 ”与“?
”与“?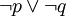 ”的两个命题也是如此。
”的两个命题也是如此。
在同一思维过程中,如果对表述的两个互为矛盾的命题,或者两个具有下反对关系的命题,既不肯定这个,又不肯定那个就要违反排中律的要求。违反排中律的要求而产生的逻辑错误,称为“模棱两可”或“模棱两不可”。
例如,历史上托洛茨基在混布尔什维克党的时候,对自己过去那些反对党的思想所作的声明“我加入布尔什维克党这件事实本身…,已经证明,我已经把过去所有那些使我和布尔什维主义分开的东西放在党的门口了”。托洛茨基既不说“把过去所有那些使我和布尔什维主义分开的东西”抛掉了,也不说对那些东西不抛掉,而知识给出一个含糊不清词项“放在党的门口”,这样的表述就违反了排中律的要求,犯有“模棱两可”的逻辑错误。这是一种以含混的语句违反排中律的方式。又如有人陈述自己的思想说,“说任何事物都不是绝对静止的,这我不同意。但说有的事物是绝对静止的,恐怕也不正确”。这种说法,显然是对“任何事物都不是绝对静止的”和“有的事物都是绝对静止的”这两个矛盾命题的同时否定,当然是违反排中律,犯有“模棱两不可”的逻辑错误。应当注意的是,在排中律的实际运用中,对具有矛盾关系的两个命题固然可以由肯定推否定,并且由否定推肯定,但对具有下反对关系的命题,却只能由否定推肯定,而不可由肯定去推否定。
排中律的作用在于保证思维表述的明确性。只有遵守排中律的要求,才能正确地进行思维表述, 才能正确地进行思维。因此,排中律是正确思维的必要条件。此外,排中律也是间接论证的逻辑依据,当我们难以从正面去证明某个命题时,常常可以通过证明该命题的矛盾命题或具有下反对关系的命题为假,从而由不能都假的特征推出原命题的真。
要正确地运用或理解排中律,应当注意下述几点。
首先,从形式上说,排中律仅仅是正确的思维表述从而是正确思维的必要条件。因此,遵守了排中律的要求,思维表述从而思维本身也仅仅是可能正确的,其最终是否正确还要取决于正确思维的其它必要条件。
其次,排中律同逻辑形式的其它基本规律一样,都是在一定的条件才能产生影响的。固然每一条基本规律都有自己特殊的条件,但决不可以此忽略它们的共有前提,即同一时间、同一场合、同一关系、同一对象等等这些反映同一思维过程的因素。
第三,排中律反映的是思维表述的方法而不是世界观,因此,排中律并不否认客观事物本身状态的多样性,排中律所要排除的,只是人们在思维表述上的居中骑墙,模棱两可,使我们关于对象某一方面的思想表述成为明确的表述。
第四,排中律在其实际应用中,对那些因客观或主观条件尚不成熟,因而不能断定的问题,并不排除采取“二不择一”的表述方式。所谓客观条件不成熟,是指认识对象还处于发展变化的过程中,人们从某一角度对其认识因此还不可能有定论。例如对“非典”的预防,我们对命题“非典的预防有特效药或者没有特效药”的任何一支,都不能如排中律所要求那样作出明确的回答,但此时的“二不选一”的回答是并不违反排中律的。 所谓主观条件不成熟,是指认识对象的发展变化虽然已处于相对静止的阶段,事物本身的属性、与其他事物之间的关系等等都已经是可以确定的了,但人们本身的认识水平并没有跟上事物的发展,人们对事物的认识还处于不能断定的状态。例如,对“火星上有生命还是无生命?”的回答,它实际上涉及到对命题“火星上有生命或者无生命”支命题的选择,当然是一个涉及排中律的问题。但这里的回答却不能简单地是“有”或者“没有”,因为从主观来说,火星的情况虽说是处于相对稳定的阶段,但人们的认识水平则因科学技术的限制尚不能达到对火星真实情况的认识,所以在上述问题的回答中我们只能“二不选一”
最后,排中律在复杂问语的处理上是没有制约作用的。所谓复杂问语,是在疑问句中隐含了某种假设的问句,如“你杀了他是不是心里特高兴?”此时,无论是回答“是”还是“不是”,你都实际上承认了那个隐含的假设即“你杀了他”。。对这样的问句,我们避开问题的肯定和否定,而针对问题中的假设予以说明,就不能说是违反了排中律。
1、在8个同样大小的杯中有7杯盛的是凉开水,1杯盛的是白糖水。你能否只尝3次,就找出盛白糖水的杯子来?
解:第一步:把8个杯子分为4、4二组,在二组中各选出一杯水,把这组中的其他水都倒一点到这个杯子里,品尝这二杯水,选出有糖水的那一组。第二步:在有糖水的这组中,把中3杯没有掺水的杯子中取出二杯水,进行第一步,判断糖水是否在这二杯中。 第三步:糖水在这二杯水中,品尝其中没有掺水的那杯,就可以知道糖水是那杯。反之也可推出糖水是另外二杯中的那一杯。
2、某药店收到10瓶药,每瓶中装有重100毫克的药丸1000粒。后被告知其中一瓶药发错了,错药的形状、颜色及包装均与其它9瓶药完全相同,只是每丸药重110毫克,你能用天平一次称出错药吗?
解:把瓶子编上号,然后从各瓶中拿出与编号相同数的药粒。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 100 | 200 | 300 | 400 | 550 | 600 | 700 | 800 | 900 | 1000 |
如果都是正确的则应有5500毫克,其中第5瓶是错的则总重为5550毫克,如果第6瓶是错的则应重5560毫克。
下边有10个不同的字母,代表(0—9)10个不同的数码已知D=5,求其余字母各代表什么数码?
D=5 ∴T=0 有一个很特殊的式子Q+E=Q 显然,E=0才能满足,但T=0,E不能重复等于0,E+1=0有进位。E=9,A+A=E,A不能是分数,又有进位。A=4 ∴2L+1=R﹥10。G+D=R,R是个位数,又是奇数R ﹥5,∵D=5,E=9, ∴R只能等于7。N+R=B ﹥10,还剩下2、3、6,N=6,B=3,Q=2。这里运用的是逻辑思维的综合分析的方法。
A=4 B=3 D=5 E=9 R=7 N=6 Q=2 L=8 T=0 G=1
评论(共46条)
呵呵,国人对概念以及之间的关系总是梳理不清,这实际上证明了逻辑思维能力不足!例如,关于逻辑思维的定义,关于逻辑思维和创新思维的关系,呈现出表面、混沌的认识!
评价按钮有bug呀,可以连续点多次。
您说的是推荐按钮吧?虽可以点多次,但是只记录一次,您可以刷新后查看。
逻辑与现象本质哲理化价值观控到人的思维罹念、理性的价值观本就都是与生俱有、只不过是前后左右的次序不一样罢了、逻辑性只非是某种反谴出来的一个描述、哪里说得如此夸浮悬殊、使生动而已.
1,天平可以称出重量吗?它本身只是看两个东西谁重谁轻的,要陪砝码才可以称重。 2,打开了瓶子的药,谁还回去买?打开称重本身就不符合原则。 3,要那么麻烦的数出那么多的数量,还不如多称几次。还可以不用砝码。
白开水与糖水分辨: 1、8个杯子编号,将前四个和后四个分为两组,先将前四个混合在一起品尝,如果有甜味,则锁定前四个,再分为两组混合品尝(1+2、3+4),品尝后锁定两杯,再次品尝,搞定 2、若前四个无味,则锁定后四位,同理分为两组混合品尝(5+6、7+8),品尝后锁定两杯,再次品尝,搞定
逻辑训练题还挺有趣的。不过上面关于药品重要区分的话是不是可以直接拿瓶子上去称,或只倒出一颗药粒也可以知道重量。如果能加入一些更加经典的例题,在每道题后面加以说明详细的规则,另外一点,如果在每道题的结果上都能加上一些文字说明能证明属于哪种逻辑方式可能会更好。
1,天平可以称出重量吗?它本身只是看两个东西谁重谁轻的,要陪砝码才可以称重。 2,打开了瓶子的药,谁还回去买?打开称重本身就不符合原则。 3,要那么麻烦的数出那么多的数量,还不如多称几次。还可以不用砝码。
2,是一瓶一瓶的称。3,这个题目只是在锻炼思维,在现实中不必定合理。
白开水与糖水分辨: 1、8个杯子编号,将前四个和后四个分为两组,先将前四个混合在一起品尝,如果有甜味,则锁定前四个,再分为两组混合品尝(1+2、3+4),品尝后锁定两杯,再次品尝,搞定 2、若前四个无味,则锁定后四位,同理分为两组混合品尝(5+6、7+8),品尝后锁定两杯,再次品尝,搞定
在计算机领域,这是 2 分查找的思想呀。。莫非你是。。
1,天平可以称出重量吗?它本身只是看两个东西谁重谁轻的,要陪砝码才可以称重。 2,打开了瓶子的药,谁还回去买?打开称重本身就不符合原则。 3,要那么麻烦的数出那么多的数量,还不如多称几次。还可以不用砝码。
我想到了一个方法:在天平两边的托盘都各放上五瓶药,加的时候放慢速度,两边各一瓶的加,加到有一边比另一边沉时(两边的药瓶数量要相同),则沉的那边最后加上的药瓶就是所要找的了。很简单哟、嘻嘻
对于逻辑思维训练第1题,“119.57.40.* 在 2012年12月20日 17:29 发表”说法正确。 本题应该是使用二分法来确定有糖水的杯子。文中的解答第二步是有问题的,不能选3个“没有掺水的杯子”(你怎么知道被掺水的杯子就不包含糖水),对第二步,应该是确定有糖水的4个杯子中选2个混合后进行判断,排除掉2个;第三步,对剩下的最后两个杯子不混合,品尝其一即可确定有糖水的杯子。
太好了.这是我发现的最全面的逻辑思维资料.
这也叫最全面,冰山一角,九牛一毛而已
我想到了一个方法:在天平两边的托盘都各放上五瓶药,加的时候放慢速度,两边各一瓶的加,加到有一边比另一边沉时(两边的药瓶数量要相同),则沉的那边最后加上的药瓶就是所要找的了。很简单哟、嘻嘻
可他说的只称要一次呀
黄金法则:
演绎推理的逻辑特征是:如果前提真,那么结论一定真,是必然性推理;









太好了.这是我发现的最全面的逻辑思维资料.