对数曲线预测法
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
[编辑]
什么是对数曲线预测法[1]
对数曲线预测法是指根据预测对象具有对数曲线变动趋势的历史数据，拟合成一条对数曲线，通过建立对数模型进行预测的方法。
[编辑]
对数曲线预测法的应用[1]
(一)模型特征和适用范围
对数曲线的模型为
(1)
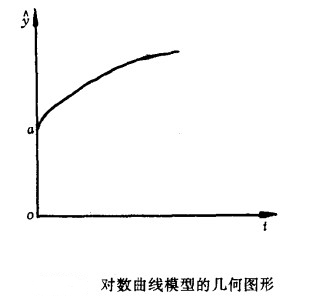
其图形如图所示。
对数曲线在图形上呈现为一条单调递增的曲线，并且增长速度逐渐减慢，这种趋势正符合那种不断增加，但增长速度却不断减小的预测对象。
(二)参数a，b的求法
要利用对数曲线模型来预测对数的趋势值，则必先求参数a，b。要求a，b，则只需将t的对数(1nt)看成是一个变量T，则指数曲线模型即可转化成一个直线模型。
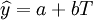(2)
这样我们就可用直线模型中求参数。和6的方法来求a,b。
如：利用最小二乘法可推a，b为
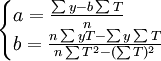
将T=lnt化入上式可得
因此，我们一旦求出参数a和b，即可确定模型进行预测。
[编辑]
对数曲线预测法的适用条件[2]
预测对象的增长趋势近似于对数函数曲线，并且在预测期限内不会发生突变。
[编辑]
对数曲线预测法的实例分析[1]
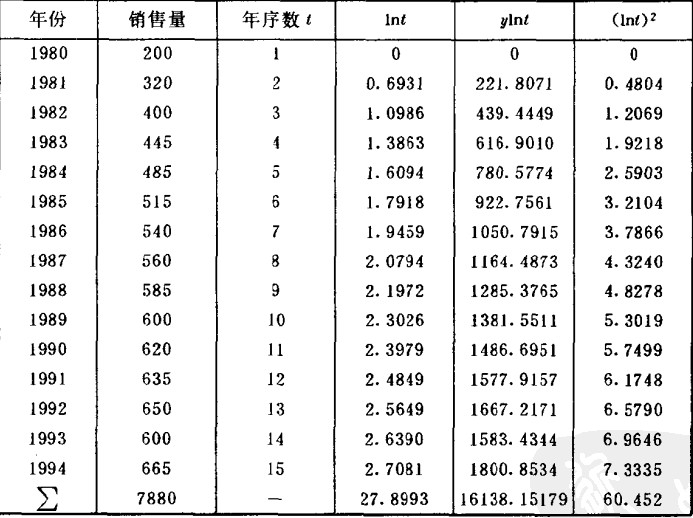
例某地区自1980-1994年彩色电视机的销售量如表所示，试预测1995年的销售量。
| 年份 | 1980 | 1981 | 1982 | 1983 | 1984 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 |
| 销售量 | 200 | 320 | 400 | 445 | 485 | 515 | 540 | 560 | 585 | 600 | 620 | 635 | 650 | 660 | 665 |
由该地区1980-1994年彩电销售的历史数据可以看出，这15年来，彩电的销售量一直在不断的增加。但逐年的增长量却是在不断减少，即增长速度在不断递减。因此，我们可以利用对数曲线预测法来研究其发展趋势，预测其他年度的销售量。
若取1980-1994年的年序数t分别为l，2，3，…，15则可列表计算出相应数据(见下表)。
[编辑]
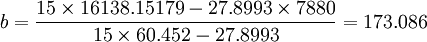
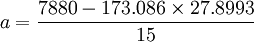
求b的例子公式都套错了，误导了一大帮人啊。。。