复制性卖权策略
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
欧式保护性期权策略从理论上看似乎是无懈可击,同时是简便易行,但它有一个十分严格的隐含假设,即市场上存在有以风险资产组合S为标的资产的欧式看跌期权。另外该期权的期限与投资者的保险期一致。这实际上是很难做到的。因此,它的实际运用的可能性和有效性就大打折扣。Rubinstein &Leland(1981)设计出了复制性卖权,弥补了欧式卖权不足的地方,为OBPI 类投资组合保险开辟了新的领域。
复制性卖权策略的基本思想为,通过数学变换,将欧式保护性期权中的S和put的组合变为只有无风险资产和风险资产的组合,这样一来,在理论上,投资者就毋须具有合适的协定价和期限的欧式看跌期权,而同样可以达到欧式保护性期权策略对冲风险的目的。
具体数学模型如下所示:
V = S + P
其中S为风险资产组合,P为欧式卖权,V为组合保险。
由Black & Scholes(1973)推导出的无套利均衡的欧式看跌期权的定价模型:
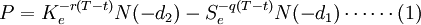
持有股票组合之投资者,若同时持有一保护性卖权,其含卖权之组合价值如下:
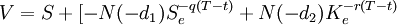
![=[1-N(-d_1)]S_e^{-q(T-t)}+N(-d_2)K_e^{-r(T-t)}](/w/images/math/b/6/9/b69aeac77fea2f16aeac7c231f02ede2.png)
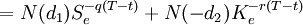
![=N(d_1)S_e^{-q(T-t)}+[ 1-N(d_2) ]K_e^{-r(T-t)}](/w/images/math/e/e/f/eefee3910ac29e5c144e1c7c98d34bbe.png)
由该式可看出受保组合之价值效果可由投资N(d1)百分比的现货股票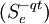 与1 − N(d2)的无风险债券
与1 − N(d2)的无风险债券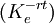 之组合来复制。例如投资者目前持有价格为S 之股票,欲将其价值在T 时保有不抵于K 之水平,此时它只要维持手中持股N(d1)的比例,而将1 − N(d1)比例之股票以当时价格出售,并将所得金额转投于无风险债券。但随着时间改变,S、t 的变动,会使得N(d1)也随之变化,例如,当股价上涨时,d1值增加使得N(d1)也增加,投资者必须增持股票,亦即必须出售无风险资产,并以出售无风险资产所获得的资金,供应增加持股之需;若遇股市下跌之际,则降低持股,并将出售股票所得转投资于无风险资产,以符合自我融资(Self-financing)的特性。
之组合来复制。例如投资者目前持有价格为S 之股票,欲将其价值在T 时保有不抵于K 之水平,此时它只要维持手中持股N(d1)的比例,而将1 − N(d1)比例之股票以当时价格出售,并将所得金额转投于无风险债券。但随着时间改变,S、t 的变动,会使得N(d1)也随之变化,例如,当股价上涨时,d1值增加使得N(d1)也增加,投资者必须增持股票,亦即必须出售无风险资产,并以出售无风险资产所获得的资金,供应增加持股之需;若遇股市下跌之际,则降低持股,并将出售股票所得转投资于无风险资产,以符合自我融资(Self-financing)的特性。







