加权移动平均法
出自 MBA智库百科(https://wiki.mbalib.com/)
加权移动平均法(weighted moving average method/weighted moving average)
目录 |
加权移动平均法就是根据同一个移动段内不同时间的数据对预测值的影响程度,分别给予不同的权数,然后再进行平均移动以预测未来值。
加权移动平均法不像简单移动平均法那样,在计算平均值时对移动期内的数据同等看待,而是根据愈是近期数据对预测值影响愈大这一特点,不同地对待移动期内的各个数据。对近期数据给予较大的权数,对较远的数据给予较小的权数,这样来弥补简单移动平均法的不足。
加权平均法的计算公式如下:
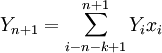
式中:
Yn + 1——第n+1期加权平均值;
Yi——第i期实际值;
x_i——第i期的权数(权数的和等于1);
n——本期数;
k——移动跨期;
用加权移动平均法求预测值,对近期的趋势反映较敏感,但如果一组数据有明显的季节性影响时,用加权移动平均法所得到的预测值可能会出现偏差。因此,有明显的季节性变化因素存在时,最好不要加权。
案例一:加权移动平均法应用高校教师的考核业绩[1]
当前,在高校薪酬分配中,一般对教师通过简单统计年度业绩考核结果来确定岗位津贴标准进行分配。笔者认为,这种办法存在着很大的弊端,如年度科研业绩的大起大落自然会造成教师收入水平的巨大波动,由此引起教师情绪上的波动以及其工作情境的变化,影响到工作效率,影响师资队伍的稳定。用改进的加权移动平均法统计教师业绩,并以此作为年度考核的依据将有效地消除年度考核业绩的“大年”与“小年” 的现象,稳定教师的业绩水平与收入水平,从而有助于吸引人才与稳定现有教师队伍。本文尝试着将加权移动平均法的“修匀”或“平滑”作用,应用于高校的年度业绩考核,使不规则的序列数据,能够平滑起来,利用经过修匀的年度考核数据作为有关津贴和奖金发放的依据,能够使教师的收入水平保持相对的稳定。
一、模型的讨论
加权移动平均法常用于进行趋势的预测,用这种办法可以得到一个光滑的修正序列,即所谓的“修匀”。把修匀的功能应用于整理高校教师年度考核的序列数据应该同样有效。
1.加权移动平均模型
加权移动平均模型是对移动平均模型的改进。采用加权移动平均,既可以做到按数据点的顺序逐点推移,逐段平均,使不规则的数据点形成比较平滑的排列规则,又可以通过权数的设定使离考核期距离不同的数据,所起的作用不同。
加权移动平均法的统计模型为:
Mt = a1Yt − 1 + a2Yt − 2 + anYt − n (1)
式中:t——时间序列下标;
Mt ——第t期的移动平均数;
Yt ——第t期的观察数据;
n——移动步长;
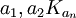 ——权数。
——权数。
2.数据的选取
(1)Yt的选取
选取某大学商学院中某位教师的业绩考核数据作为样本,因该学院对按业绩决定教师报酬的做法执行得比较早且比较彻底,该教师从刚到学院工作至今有13个年头,所以,所选取的数据样本基本满足作移动平均的要求,可以用来阐明用移动平均法来计算年度考核业绩的合理性。
(2)n的选取
移动步长n的大小对移动平滑结果起决定性作用,选好n是加权移动平均法的关键。n值取得太小,模型灵敏度高,能较灵敏地反映近期的变化趋势,但也可能对随机干扰反映过度灵敏,据此得到的考核数据起伏剧烈,从而可能造成对被考核对象的误判;n取得大时,对时间序列中包含的随机变动的敏感性过低,以致不能敏锐地反映近期的变化趋势,甚至会造成被考核对象在一段时间范围内不努力但考核结果依然好的现象,如此也会造成对被考核对象的误判。所以,在n的选取上,必须结合教师的教学尤其是科研工作的特点和业绩考核的要求,以及各高校在考核方面的综合实践。这里,将n设定为3。
(3)a1,a2,a3,的选取
为了使考核能够更好地发挥激励作用,在选取权数的时候,应使离考核期越近的权数越大。权数的选取,听取了一些教育专家的建议,在综合各方面的建议后,将分别a1,a2,a3分别设定为0.5、0.3和0.2。
这样,用来计算考核业绩的加权移动平均模型为:
Mt = 0.5Yt − 1 + 0.3Yt − 2 + 0.2Yt − 3 (2)
二、模拟计算及分析
1.利用加权移动平均计算的结果及分析
将各年度考核数据与根据公式(2)算得的加权移动平均数列入表1中。
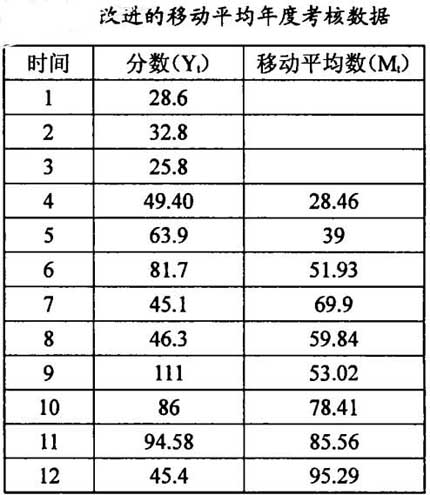
利用表1中数据绘得曲线,如图:
上图中的系列2曲线(加权移动平均曲线)明显的比系列1曲线平缓,并且在所设定的情况下,更能体现上升的趋势。所以利用系列2的加权移动平均数据代替系列1的简单年度考核数据,能够有效地避免出现与考核业绩挂钩的津贴和奖金大起大落的现象,即修匀的效果比较显著。
但上述方法,也存在明显不合理的情况:
(1)在移动步长取3的情况下,系列2的数据只能从第4年才开始,前三年都是空白(见上表的第3列)。而许多高校的考核一般都是从第1年就开始,第2年年初就开始与津贴挂钩,即次年的津贴发放是根据前一年的考核成绩。对于前三年出现空白考核业绩的情况,在实际考核工作中,显然不能接受。
(2)系列2出现明显的滞后情况,如在第7年末和第12年末的年度实际考核业绩很低,但加权移动平均得分却非常高;而在第9年末的考核分数很高,但加权移动平均得分却很低,明显不合理。这种现象称为加权移动平均的“滞后”现象。
2.改进的加权移动平均模型
改进加权移动平均模型的目的,是使在考核中应用该模型时,能够继续保持修匀与平滑的作用,又能够避免滞后现象的发生。实际上在使用模型的目的仅仅是为了考核的特定情况下,只是对加权移动平均模型(2)稍加调整就可以满足需要了。
在移动步长仍取3的情况下,将根据模型(2)算得的移动平均值向前移动一年,这样,从第3年就有了移动平均得分,将滞后三年的情况改为滞后两年。这样改进后的加权移动平均公式就变为:
Mt = 0.5Yt − 0 + 0.3Yt − 1 + 0.2Yt − 2 (3)
根据改进的移动平均模型(3)算得的加权移动平均值如表2。
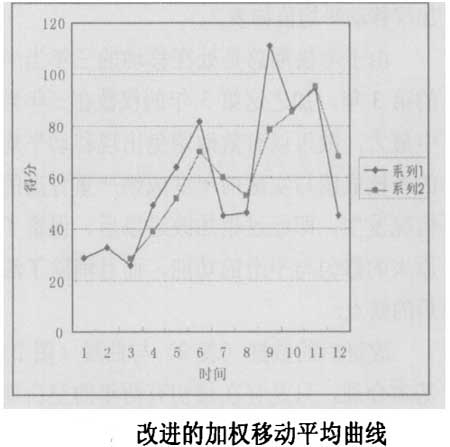
由于考核期总是处在移动的三年当中的第3年,加之这第3年的权数在三年当中最大,故可以有效地避免出现移动平均的考核成绩与实际的年度成绩严重背离的情况发生,即经过稍加改进以后,保留了原来的修匀与平滑的功能,而且消除了滞后的缺点。
改进后的数据(下表)与曲线(下图)基本合理,只是存在最初有两年的空白期问题。但是,在基本趋势相同的情况下,可以取第1年与第2年末的实际得分作为来年津贴与奖金发放的依据,然后,从第3年开始就可以接上改进的加权移动平均的考核分数了。如果考虑到新进青年博士教师科研启动等的时间性问题,因而在最初的两年当中只是作年度考核,但不与津贴与奖金挂钩,到第三年以后再与津贴与奖金挂钩的话,也许两年空白期的矛盾就不存在了。
三、结论与建议
通过上述分析,得出如下结论:
1.简单的年度考核业绩往往是上下起伏不定的;
2.用加权移动平均的年度业绩考核成绩来代替简单的年度考核成绩能有效地避免起伏波动的现象,即能够做到修匀与平滑;但造成与实际的年度业绩严重背离的情况,即出现滞后现象;
3.用改进的加权移动平均年度考核成绩取代简单的年度考核成绩,不仅可以有效避免大起大落的波动,而且还可以避免与实际的年度业绩背离的情况发生。
所以,用改进的加权移动平均法来统计高校教师的年度考核成绩,并以此作为有关津贴与奖金发放的依据,能够有效地排除由于某一年当中科研业绩不佳造成实际年度考核成绩差,从而津贴或奖金骤然减少,给教师带来的不良心理影响。
- ↑ 山鸣峰,李双,杨国宏.用改进的加权移动平均法统计高校教师的考核业绩[J].《中国高校师资研究》.2006,03









突然发现MBAlib好强大啊,比百度百科强太多了。