凯恩斯的流动偏好理论
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
按照凯恩斯的观点,作为价值尺度的货币具有两种职能,其一是交换媒介或支付手段,其二是价值贮藏。货币需求就是人们宁愿牺牲持有生息资产(如各种有价证券)会取得的利息收入,而把不能生息的货币保留在身边。至于人们为什么宁愿持有不能生息的货币,是因为与其他的资产形式相比,货币具有使用方便灵活的特点,是因为持有货币可以满足三种动机,即交易动机、预防动机和投机动机。所以凯恩斯把人们对货币的需求称为流动偏好(Liquidity Preference)。流动偏好表示人们喜欢以货币形式保持一部分财富的愿望或动机。
流动偏好理论的内容[1]
(一)交易动机(The Transaction Motive)
交易动机是指人们为了应付日常交易的需要而持有一部分货币的动机。在任何收入水平上,无论是家庭还是厂商都需要作为交易媒介的货币。因为就个人或家庭而言,一般是定期取得收入,但经常需要支出,例如家庭需要用货币购买食品、服装,支付电费和燃料费用等,所以为了购买日常需要的生活资料,他们经常要在手边保留一定数量的货币。就厂商而言,它们取得收入(货款)也是一次性的,但是为了应付日常零星的开支,如购买原材料,支付工人工资,它们也需要经常保持一定量的货币。例如,一个家庭每月月初收入为900元人民币,假定该家庭每日平均日常支付为30元,那么它将在月末全部用完这笔收入。该家庭平均每天持有的货币量是30元,也就是说,为了应付日常交易需要,该家庭需要每天平均持有30元人民币,否则就会出现支付困难。可见,为了日常交易而持有货币,是因为人们的收入和支出并不是同时进行的。个人或者家庭的收入和支出的时间越是接近,为了交易的目的而平均留在身边的货币就越少。
由交易动机引起的货币需求量还跟人们的收入水平密切相关。当人们的收入增加时,人们的消费水平会有所提高,消费量增大,从而人们满足日常交易所需的货币量也增加。由此可见,由交易动机所引发的货币需求是收入的增函数,随着收入的增加而增加。对货币的交易需求也容易受到持币成本的影响,也就是会受到利息率高低的影响。因为人们在确定交易所需保持的货币时,不仅需要考虑持有货币对便利交易的好处,也要考虑到持有货币会损失的利息。但是一般认为,家庭的货币交易需求量大致上不受利率波动的影响。利率对货币交易需求的影响主要见之于企业。企业的银行存款数目较大,如果它们静观利率的变化而不对存款方式做出相应的调整的话,损失会很大。因此,在高利率的情况下,企业会在寻求保持最低限度的交易货币方面下功夫,即所谓的“现金管理”。根据美国经济学家威廉·杰克·鲍莫尔(William Jack Baumol)的研究,人们或者企业最优的对货币的交易需求与利率的平方根的倒数成正比。但是因为在一般情况下,利率对出于交易动机的货币需求影响较小,人们仍然把交易需求看成是收入的函数而忽略利率的影响。
如上所述,出于交易动机的货币需求,虽然收入和支出的时间间隔因人而异,因企业而异,但是从全社会来看,总的时间间隔的平均数以及由此决定的货币流通速度取决于诸如支付习惯、社会经济的发展水平以及其他的制度性因素,因而在短期内可以看成是稳定的,所以我们在进行短期均衡分析时,一般把出于交易动机的货币需求视为收入水平的线性函数,两者具有固定比例关系。
(二)预防动机(The Precautionary Motive)
预防动机是人们为了预防意外的支付而持有一部分货币的动机。即人们需要货币是为了应付不测之需,如为了支付医疗费用、应付失业和各种意外事件等。虽然个人对意外事件的看法不同,从而对满足预防动机需要的货币数量有所不同,但从整个社会来说,货币的预防需求与收入密切相关。因而由预防动机引发的货币需求量也被认为是收入的函数,与收入同方向变动。
当然,无论是出于交易动机还是出于预防动机的货币需求,在一定程度上还取决于利息率的高低。因为持有货币而不是生息资产将损失利息收入,利息率越高,持有货币牺牲的利息越多,因而货币的需求越少,两者呈反方向变化。但是,为了简化分析,我们假设,出于交易动机和预防动机的货币需求惟一地取决于收入水平的高低。因为货币的交易需求和预防需求都被认为是收入的函数,所以可以把两者结合起来进行考察。把两种货币需求合起来用L1表示,用Y表示收入,这种函数关系可写成:L1 = L1(Y)。这个函数所强调的是交易货币需求(包括预防需求)是收入的函数,它同利率无关。如下图所示:在货币需求—收入坐标图中交易货币需求曲线是一条过原点的射线;而在货币需求—利率的坐标图中,它则是一条垂直线。
图:货币的交易需求和预防需求
(三)投机需求(The Speculative Motive)
人们之所以宁愿持有不能生息的货币还因为持有货币可以供投机性债券买卖之用。投机动机是人们为了抓住有利的购买生息资产(如债券等有价证券)的机会而持有一部分货币的动机。我们知道,一般而言,债券价格与利息率之间存在着一种反方向变动的关系,即:债券价格=债券固定利息收益/市场利息率。显然,市场利率上升,债券价格下降;市场利率下降,债券价格上升。
如某种面值为100 元,固定利息率为5%的债券,在市场利息率为5%时,其价格为100×5%÷5%=100(元)。当市场利息率上升为6%时,这张债券的价格将变为100 ×5%÷6%=83.33(元);而当市场利息率下降为4%时,这张债券的价格将变为100×5%÷4%=125(元)。
正是利息率与证券价格之间的这种反方向的变动关系使得利息率对投机性的货币需求有了决定性的影响。凯恩斯指出,在任一时刻,人们心目中有着某种“标准”的利息率。如果市场利率高于“标准”的利息率,在这种场合下他认为市场利率将会下降,也就是债券的价格将会升高,于是他就会买进债券,以便日后利率下降、债券价格上涨时再卖出债券换回货币。反之,如果市场利率低于“标准”的利息率,在这种场合下他认为市场利率将会上升,也就是债券的价格将会下降,于是他就会卖出债券换回货币,以便日后利率上升、债券价格下跌时再买进债券。由此可见,出于投机动机的货币需求是利息率的减函数,较低的利率对应着一个较大的投机货币需求量,较高的利率则对应着一个较小的货币需求量。用L2表示出于投机动机的货币需求,r表示利息率,则上述函数关系可表示为:L2 = L2(r),L2'<0。
我们可以发现两种极端情形。其一,假如利率非常高,人们预期日后利率只跌不涨(债券价格则只会上涨),这时,人们就会将手中持有的可用于投机的货币全部换成债券,从而其投机性货币需求L2=0;另一种极端就是当利率非常低时,人们预期利率不可能再低下去了,也就是人们预期利率将会上涨,债券未来价格只会下跌。在这种场合下,人们必将卖出债券以持有货币,并不再购买债券,有多少货币就持有多少货币。这种情形被称为“流动性陷阱”(Liquidity Trap)或者“凯恩斯陷阱”。在“流动性陷阱”的情况下,投机性货币需求的利率弹性为无穷大,货币需求曲线在利率降为r0时变成一条与横轴平行的直线。如下图所示。
图:投机性货币需求
虽然我们可以分别研究货币需求的交易动机、预防动机和投资动机,但是个人出于哪种动机而持有货币是很难分得清楚的,同样一笔货币可以用于任何一种动机。这三种动机都会影响个人对货币的持有量,并且当其他资产形式的获益提高时,对于货币的需求将下降。
(四)货币的总需求
综上所述,货币的总需求可以表述为:
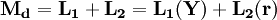
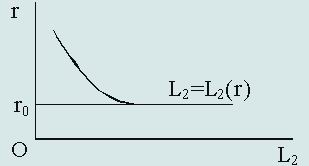
下图(a)中的垂直线L1表示交易动机和预防动机引发的货币需求,它与利率无关,由国民收入决定,因而垂直于横轴。下图(b)表示货币的投机需求,它与利率反方向变动。下图1(c)表示相同利率水平处的(a)与(b)部分之和构成对货币的总需求。
图:货币的总需求
评论(共11条)
想問一下,有關平均每天持有貨幣量的問題。 平均每天持有貨幣量應該是900/2=450吧?(900+870+.....+0)/30
想問一下,有關平均每天持有貨幣量的問題。 平均每天持有貨幣量應該是900/2=450吧?(900+870+.....+0)/30
修正一下,是(900+870+840+.....+0)/31=450 舉例:100元每天花25元,5天用完,平均5天餘額為:(100+75+50+25+0)/5=50(100/2=50) 若改為一天花50,3天用完,則每天貨幣平均持有量:(100+50+0)/3=50(100/2=50) 以此類推若是分30天花完,平均每天花3.33元,則每天貨幣平均持有量結果應該也是100/2=50
最后一张图中的图(c)有点问题吧?没有反映出(a)中的需求量。
谢谢指正,更换了一张图片,希望对你有帮助~
谢谢~正好学到宏观经济学货币需求这块,被利率和货币投机需求搞得很晕。这篇是我看到的最清楚易懂的了,真感谢呀
修正一下,是(900+870+840+.....+0)/31=450 舉例:100元每天花25元,5天用完,平均5天餘額為:(100+75+50+25+0)/5=50(100/2=50) 若改為一天花50,3天用完,則每天貨幣平均持有量:(100+50+0)/3=50(100/2=50) 以此類推若是分30天花完,平均每天花3.33元,則每天貨幣平均持有量結果應該也是100/2=50
5天用完? 100元 每天25元? 用离散点求均值 时间有些问题 逻辑上不严谨的样子 用连续的思维 求均值 较容易理解 期初100元 期末0元 中间以直线法折扣 均值为 (100+0)/2=50
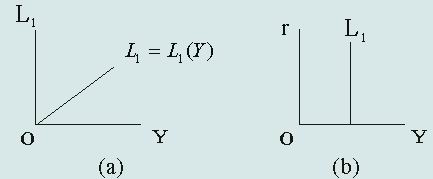








谢谢,图文很清楚