方差
出自 MBA智库百科(https://wiki.mbalib.com/)
方差(Variance)
目錄 |
方差是各個數據與其算術平均數的離差平方和的平均數,通常以σ2表示。方差的計量單位和量綱不便於從經濟意義上進行解釋,所以實際統計工作中多用方差的算術平方根——標準差來測度統計數據的差異程度。
標準差又稱均方差,一般用σ表示。方差和標準差的計算也分為簡單平均法和加權平均法,另外,對於總體數據和樣本數據,公式略有不同。
設總體方差為σ2,對於未經分組整理的原始數據,方差的計算公式為:
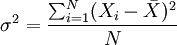
對於分組數據,方差的計算公式為:
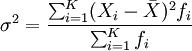
方差的平方根即為標準差,其相應的計算公式為:
未分組數據: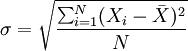
分組數據: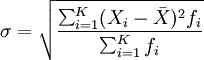
樣本方差與總體方差在計算上的區別是:總體方差是用數據個數或總頻數去除離差平方和,而樣本方差則是用樣本數據個數或總頻數減1去除離差平方和,其中樣本數據個數減1即n-1稱為自由度。設樣本方差為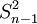 ,根據未分組數據和分組數據計算樣本方差的公式分別為:
,根據未分組數據和分組數據計算樣本方差的公式分別為:
未分組數據: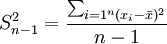
分組數據: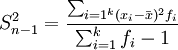
未分組數據: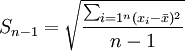
分組數據: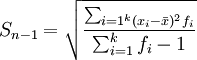
例:考察一臺機器的生產能力,利用抽樣程式來檢驗生產出來的產品質量,假設搜集的數據如下:
| 3.43 | 3.45 | 3.43 | 3.48 | 3.52 | 3.50 | 3.39 |
| 3.48 | 3.41 | 3.38 | 3.49 | 3.45 | 3.51 | 3.50 |
根據該行業通用法則:如果一個樣本中的14個數據項的方差大於0.005,則該機器必須關閉待修。問此時的機器是否必須關閉?
解:根據已知數據,計算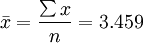
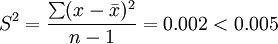
因此,該機器工作正常。
方差和標準差也是根據全部數據計算的,它反映了每個數據與其均值相比平均相差的數值,因此它能準確地反映出數據的離散程度。方差和標準差是實際中應用最廣泛的離散程度測度值。
評論(共36條)
一個房間的風速與溫度,測量一組數據,那這是屬於樣本方差還是總體方差
顯然是樣本方差
一個房間的風速與溫度,測量一組數據,那這是屬於樣本方差還是總體方差
“一個”說明是整體 而且一個房間裡面的空間的風速與溫度都可能是不一樣的 故寡人認為測的是總體方差 是相對於這一個房間“總體"而言的
有的說是除以N,有的又說是N-1。為什麼?
除以N是應用於全部的數據,而除以N-1是應用於樣本。
為什麼總體方差與樣本方差的自由度要相差1,假如把樣本看作是一個總體的話,那麼自由度豈不是要變會n?好像有點矛盾~~~
樣本均值X=(X1+X2+....+Xn)/n 樣本方差Sx=((X1-X)平方+(X2-X)平方+.....+(Xn-X)平方)/n 以上兩個不等式可以消去Xn,所以未知數只有N-1個,所以除以n-1.
∑i代表什麼??????
分組數據中i是第i組的意思,fi表示第i組的數據的個數 ∑i=1 k(xi-x拔)fi xi是組中值,乘以fi 是因為每組i個數據,相當於把每組的數據看成一樣的,由組中值xi來表示,每組有i個數據, 同樣分數線下麵的 ∑i=1 k fi 是數據的總的個數
分組數據中i是第i組的意思,fi表示第i組的數據的個數 ∑i=1 k(xi-x拔)fi xi是組中值,乘以fi 是因為每組i個數據,相當於把每組的數據看成一樣的,由組中值xi來表示,每組有i個數據, 同樣分數線下麵的 ∑i=1 k fi 是數據的總的個數
k是組數 共有k組 所以i的取值為 1 到 k
一個房間的風速與溫度,測量一組數據,那這是屬於樣本方差還是總體方差
這組數據是一個樣本,即一組數據。應該是樣本方差
“樣本均值X=(X1+X2+....+Xn)/n 樣本方差Sx=((X1-X)平方+(X2-X)平方+.....+(Xn-X)平方)/n 以上兩個不等式可以消去Xn,所以未知數只有N-1個,所以除以n-1.”
這個不太理解,有一說是自由度。都不甚明白。。
樣本方差是由樣本數量n來決定,為了使樣本方差估計的無偏性,一旦樣本均值算出,樣本的決定條件就變成了n-1,所以是除以n-1。
這些都是統計學中的基本概念啊,一般來說,商科學生大一的時候就學過了。
就你知道的多








很好~謝謝~