T檢驗
出自 MBA智库百科(https://wiki.mbalib.com/)
T檢驗(T Test)
目錄 |
T檢驗,亦稱student t檢驗(Student's t test),主要用於樣本含量較小(例如n<30),總體標準差σ未知的正態分佈資料。
T檢驗是用於小樣本(樣本容量小於30)的兩個平均值差異程度的檢驗方法。它是用T分佈理論來推斷差異發生的概率,從而判定兩個平均數的差異是否顯著。
T檢驗是戈斯特為了觀測釀酒質量而發明的。戈斯特在位於都柏林的健力士釀酒廠擔任統計學家。戈斯特於1908年在Biometrika上公佈T檢驗,但因其老闆認為其為商業機密而被迫使用筆名(學生)。
T檢驗的適用條件:正態分佈資料
目的:比較樣本均數 所代表的未知總體均數μ和已知總體均數μ0。
計算公式:
t統計量: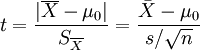
自由度:v=n - 1
適用條件:
(1) 已知一個總體均數;
(2) 可得到一個樣本均數及該樣本標準誤;
(3) 樣本來自正態或近似正態總體。
單個樣本的t檢驗實例分析[1]
例1 難產兒出生體重 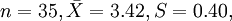
一般嬰兒出生體重μ0 = 3.30(大規模調查獲得),問相同否?
解:1.建立假設、確定檢驗水準α
H0:μ = μ0 (難產兒與一般嬰兒出生體重的總均數相等;H0無效假設,null hypothesis)
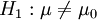 (難產兒與一般嬰兒出生體重的總均數不等;H1備擇假設,alternative hypothesis,)
(難產兒與一般嬰兒出生體重的總均數不等;H1備擇假設,alternative hypothesis,)
雙側檢驗,檢驗水準:α = 0.05
2.計算檢驗統計量
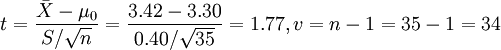
3.查相應界值表,確定P值,下結論
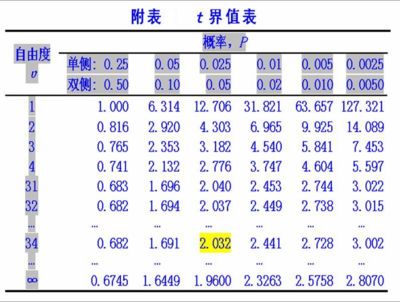
查附表1: t0.05 / 2.34 = 2.032,t = 1.77,t < t0.05 / 2.34,P > 0.05,按α = 0.05水準,不拒絕H0,兩者的差別無統計學意義,尚不能認為難產兒平均出生體重與一般嬰兒的出生體重不同
配對設計:將受試對象的某些重要特征按相近的原則配成對子,目的是消除混雜因素的影響,一對觀察對象之間除了處理因素/研究因素之外,其它因素基本齊同,每對中的兩個個體隨機給予兩種處理。
- 兩種同質對象分別接受兩種不同的處理,如性別、年齡、體重、病情程度相同配成對。
- 同一受試對象或同一樣本的兩個部分,分別接受兩種不同的處理
- 自身對比。即同一受試對象處理前後的結果進行比較。
目的:判斷不同的處理是否有差別
計算公式及意義:
t 統計量: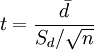
自由度:v=對子數-1
適用條件:配對資料
T檢驗的步驟[2]
1、建立虛無假設H0:μ1 = μ2,即先假定兩個總體平均數之間沒有顯著差異;
2、計算統計量t值,對於不同類型的問題選用不同的統計量計算方法;
1)如果要評斷一個總體中的小樣本平均數與總體平均值之間的差異程度,其統計量t值的計算公式為:
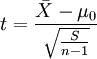
2)如果要評斷兩組樣本平均數之間的差異程度,其統計量t值的計算公式為:
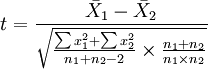
3、根據自由度df=n-1,查t值表,找出規定的t理論值併進行比較。理論值差異的顯著水平為0.01級或0.05級。不同自由度的顯著水平理論值記為t(df)0.01和t(df)0.05
4、比較計算得到的t值和理論t值,推斷發生的概率,依據下表給出的t值與差異顯著性關係表作出判斷。
| T值與差異顯著性關係表 | ||
|---|---|---|
| t | P值 | 差異顯著程度 |
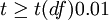 | 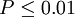 | 差異非常顯著 |
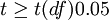 | 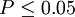 | 差異顯著 |
| t < t(df)0.05 | P > 0.05 | 差異不顯著 |
5、根據是以上分析,結合具體情況,作出結論。
例如,T檢驗可用於比較藥物治療組與安慰劑治療組病人的測量差別。理論上,即使樣本量很小時,也可以進行T檢驗。(如樣本量為10,一些學者聲稱甚至更小的樣本也行),只要每組中變數呈正態分佈,兩組方差不會明顯不同。如上所述,可以通過觀察數據的分佈或進行正態性檢驗估計數據的正態假設。方差齊性的假設可進行F檢驗,或進行更有效的Levene's檢驗。如果不滿足這些條件,只好使用非參數檢驗代替T檢驗進行兩組間均值的比較。
T檢驗中的P值是接受兩均值存在差異這個假設可能犯錯的概率。在統計學上,當兩組觀察對象總體中的確不存在差別時,這個概率與我們拒絕了該假設有關。一些學者認為如果差異具有特定的方向性,我們只要考慮單側概率分佈,將所得到t-檢驗的P值分為兩半。另一些學者則認為無論何種情況下都要報告標準的雙側T檢驗概率。
1、數據的排列
為了進行獨立樣本T檢驗,需要一個自(分組)變數(如性別:男女)與一個因變數(如測量值)。根據自變數的特定值,比較各組中因變數的均值。用T檢驗比較下列男、女兒童身高的均值。
| 性別 | 身高 | |
|---|---|---|
| 對象1 對象2 對象3 對象4 對象5 | 男性 男性 男性 女性 女性 | 111 110 109 102 104 |
| 男性身高均數 = 110 女性身高均數 = 103 | ||
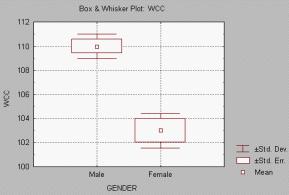
2、T檢驗圖
在T檢驗中用箱式圖可以直觀地看出均值與方差的比較,見下圖:
這些圖示能夠很快地估計並且直觀地表現出分組變數與因變數關聯的強度。
3、多組間的比較
科研實踐中,經常需要進行兩組以上比較,或含有多個自變數並控制各個自變數單獨效應後的各組間的比較,(如性別、藥物類型與劑量),此時,需要用方差分析進行數據分析,方差分析被認為是T檢驗的推廣。在較為複雜的設計時,方差分析具有許多t-檢驗所不具備的優點。(進行多次的T檢驗進行比較設計中不同格子均值時)。
- 要有嚴密的抽樣設計隨機、均衡、可比
- 選用的檢驗方法必須符合其適用條件(註意:t檢驗的前提是資料服從正態分佈)
- 單側檢驗和雙側檢驗
單側檢驗的界值小於雙側檢驗的界值,因此更容易拒絕,犯第Ⅰ錯誤的可能性大。
- 假設檢驗的結論不能絕對化
- 不能拒絕H0,有可能是樣本數量不夠拒絕H0 ,有可能犯第Ⅰ類錯誤
- 正確理解P值與差別有無統計學意義
P越小,不是說明實際差別越大,而是說越有理由拒絕H0 ,越有理由說明兩者有差異,差別有無統計學意義和有無專業上的實際意義並不完全相同
- 假設檢驗和可信區間的關係
- 結論具有一致性
- 差異:提供的信息不同
區間估計給出總體均值可能取值範圍,但不給出確切的概率值,假設檢驗可以給出H0成立與否的概率
評論(共73條)
very nice... it would be much better if you have a pair sample t-test.
查附表1: t0.05 / 2.34 = 2.032,t = 1.77,t < t0.05 / 2.34, P > 0.05,按α=0.05水準,不拒絕H0,兩者的差別無統計學意義 LZ 的意思是不是 T0.05/2(34)=2.032!,下同
第一個t的公式是不是有問題啊,錯把n寫為x了,好像…
感謝您的指正,原文已修正,並增加了新的內容,謝謝您的參與。
much thx, cannot understand in english but in Mandarin is damn simple!
和樓上有同樣疑問 2.032是哪裡來的?
查詢“t界值表”得來的~
你舉的嬰兒體重的例子算下來T<T(0.05),P>0.05,不拒絕H0,兩者的差別無統計學意義。既然差異概念不大,那最後一個結論我不知道是如何得來的,請教?
公式是錯的...Σx1²+Σx2²那裡應該是樣本一的各數據與平均數一的差的平方的和...加上樣本二的各數據與平均數一的差的平方的和...你這錯誤的公式誤人子弟``
much thx, cannot understand in english but in Mandarin is damn simple!
- many thx or thx so much
t0.05 / 2.34 = 2.032中 0.05是P 概率 但是2.34是何物啊?求解釋 plz tell me what is 2.34 among t0.05/2.34 ?0.05 is the probability that we searched in the table, but what's 2.34 stands for?
看不懂,有好多字母代表了什麼東西都沒寫出來, 如X等某些詞。。。這對外人來說都是不可理解的。
本來就是外行才來上網查,內行你還來查就呵呵了。
用簡單的方式大概講述了 T-test,一路從 常態分佈 假設檢定 Z test 信賴區間 再看到 T 會比較好懂。如果還不行,就從更前面 抽樣隨機分佈 開始看吧
其實掌握一個知識都是循序漸進的,沒有瞭解其他相關統計知識的人突然接觸會感到一頭霧水也很正常,但是這個編寫的已經非常好了,不能理解的人需要自己回去打牢基礎,在這裡怪別人有什麼用?
原文:T檢驗的步驟[2]中計算t統計量的公式 是不是錯了。。應該是t=(x-u)/s根號下(n-1)
好像沒錯吧
排版有的地方太差了,很影響閱讀 比如 "查附表1: t0.05 / 2.34 = 2.032,t = 1.77,t < t0.05 / 2.34,P > 0.05"中 為什麼不寫成 t_{0.05/2}(34)呢?








看不懂,有好多字母代表了什麼東西都沒寫出來, 如X等某些詞。。。 這對外人來說都是不可理解的。