邏輯斯蒂方程
出自 MBA智库百科(https://wiki.mbalib.com/)
邏輯斯蒂方程(Logistic Equation)
目錄 |
當一種新產品剛面世時,廠家和商家總是採取各種措施促進銷售。他們都希望對這種產品的推銷速度做到心中有數,這樣廠家便於組織生產,商家便於安排進貨。怎樣建立數學模型描述新產品推銷速度呢?
首先要考慮社會的需求量.社會對產品的需求狀況一般依如下兩個特性確定:
1. 對產品的需求有一個飽和水平.當產品需求量達到一定數量時,對這種產品的需求也飽和了,設飽和水平為a;
2. 假設在時刻t,社會對產品的需求量為x=x(t),需求的增長速度dx/dt正比於需求量x(t)與需求接近飽和水平的程度a-x(t)之乘積,記比例繫數為k ;
根據上述實際背景的兩個特征,可建立如下微分方程:
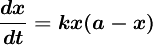 .......................(1)
.......................(1)
分離變數,得:
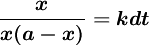
兩邊積分,得:
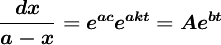
其中: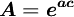
從而,通解為:
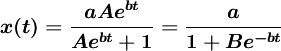 ......(2)
......(2)
其中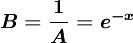 ,B和b為正常數,可由初始條件確定。式(1)稱為邏輯斯蒂方程(1ogistic equation),式(2)稱為邏輯斯蒂曲線。
,B和b為正常數,可由初始條件確定。式(1)稱為邏輯斯蒂方程(1ogistic equation),式(2)稱為邏輯斯蒂曲線。
1.當t=O時,x(t)的值為: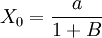 ;
;
2.x(t)的增長率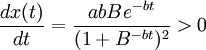 ,因此,x(t)是增函數;
,因此,x(t)是增函數;
3.當B值較大而t較小時,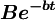 將很大,
將很大,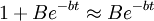 ,於是
,於是
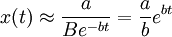
x(t)近似於依指數函數增大,銷售速度不斷增大;
4.當t增大以後,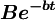 越來越接近於零,分母越來越接近於1,銷售速度開始下降,x(t)的值接近於a(飽和值)。
越來越接近於零,分母越來越接近於1,銷售速度開始下降,x(t)的值接近於a(飽和值)。
1.人口限制增長問題
人口的增長不是呈指數型增長的,這是由於環境的限制、有限的資源和人為的影響,最終人口的增長將減慢下來。實際上,人口增長規律滿足邏輯斯蒂方程。
2. 信息傳播問題
所謂信息傳播可以是一則新聞,一條謠言或市場上某種新商品有關的知識,在初期,知道這一信息的人很少,但是隨時間的推移,知道的人越來越多,到一定時間,社會上大部分人都知道了這一信息.這裡的數量關係可以用邏輯斯蒂方程來描述。若以t表示從信息產生算起的時間,P表示已知信息的人口比例,則邏輯斯蒂方程變為:
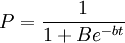 ...................(3)
...................(3)
例如,當某種商品調價的通知下達時,有10%的市民聽到這一通知,2小時以後,25%的市民知道了這一信息,由邏輯斯蒂方程可算出有75%的市民瞭解這一情況所需要的時間。
在方程(3)中,由t=0時,P=10%可得 B=9;再由t=2時,P=25%可得,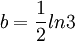 。
。
當P=75%時,有:
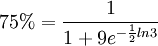
解得t=6,即6小時後,全市有75%的人瞭解這一通知。
3.商品銷售預測問題
例如,某種商品的銷售,開始時,知道的人很少,銷售量也很小。當這種商品信息傳播出去後,銷售量大量增加,到接近飽和時銷售量增加極為緩慢。比如,這種商品飽和量估計a=500(百萬件),大約5年可達飽和,常數b經測定為b=lnl0,B=100。下麵我們來預測一下第3年末的銷售量是多少。
由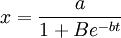 ,有:
,有:
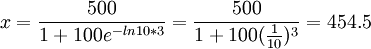 (百萬件)
(百萬件)
所以第三年末的市場銷售量大約為454.5百萬件,這樣可以做到有計劃地生產。
邏輯斯蒂方程的應用比較廣泛。如果問題的基本數量特征是:在時間t很小時,呈指數型增長,而當t增大時,增長速度就下降,且越來越接近於一個確定的值,這類問題可以用邏輯斯蒂方程加以解決。
案例一:基於邏輯斯蒂方程的垃圾郵件過濾特征方法的研究[1]
- 1.邏輯斯蒂(Logistic)方程
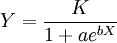 (1)
(1)
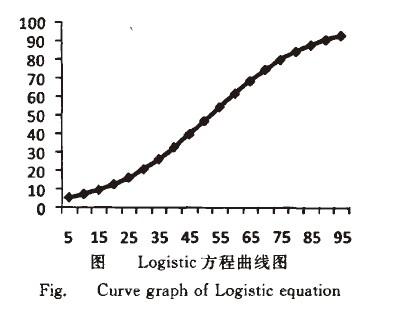
Logistic曲線其特點是開始增長緩慢,而在以後的某一範圍內迅速增長,達到某限度後,增長又緩慢下來∞3.曲線略呈拉長的“S”型.Logistic增長的速度函數圖像為單峰曲線,這表明Logistic曲線增長過程分為三個階段:慢一快一慢。
在實際中,特征項也根據重要程度的不同分為三部分,並且與Logistic曲線的三個階段相對應:第一部分是在垃圾郵件分類中貢獻甚微的特征項,特征權值不需要明顯的變化,全部是不予選擇的特征項,對應Logistic曲線變化幅度較小的第一階段;第二部分是要進行甄別的特征項,需要區別特征項重要程度強弱,特征權值變化幅度越大越有利於特征項的選擇,與曲線的變化幅度最快的第二階段對應;第三個部分是必須選取的高特征權值的特征項,對應曲線第三階段,這部分特征項同樣不需要顯著的差別,全部是要選擇的特征項.2.參數設定。
- 2.參數設定
以影響特征選擇方法的三個要素為因數,設邏輯斯蒂(Logistic)方程的參數X為:
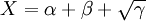 (2)
(2)
根據(8)式測定垃圾郵件中特征項集的X值分佈情況:P(X<100)>90%,即特征權值小於100的特征項占待選擇特征項集的95%以上,可判定需要甄別的特征項集中在X值小於lOO的特征項集合內,由此設定一組樣本值(X_1,Y_1),(X_2,Y_2),\cdots(\cdotsX_10,Y_10),,其數值如下表所示.以此分析此結果是否能以Logistic方程描述。
表:X,Y參數值表
| X | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 95 |
| y | 9 | 12 | 16 | 30 | 50 | 65 | 77 | 84 | 90 | 93 |
在(1)式中,當X→∞,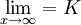 ,所以特征項重要程度的無限延長的終極量是K.假定這組值的K值為100(%),即特征項的最重要程度為100%.將(1)式移項得:
,所以特征項重要程度的無限延長的終極量是K.假定這組值的K值為100(%),即特征項的最重要程度為100%.將(1)式移項得: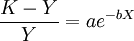 (3)
(3)
令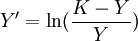 ,則由最小平方法估計的
,則由最小平方法估計的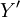 為
為
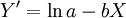 (4)
(4)
因此,Y和X對於Logistic方程的符合度,可由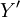 和X的線性相關係數
和X的線性相關係數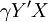 給出:
給出:
![\gamma Y^\prime X=\frac{\sum XY^\prime-\frac{1}{n}(\sum X)(\sum Y^\prime)}{\sqrt{\left[\sum X^2-\frac{1}{n}(\sum X^2)\right]\left[\sum(Y^\prime)^2-\frac{1}{n}(\sum Y^\prime)^2\right]}}=\frac{\sum xy^\prime}{\sqrt{\sum X^2\cdot\sum(y^\prime)^2}}](/w/images/math/5/d/5/5d51e451e2cbccc27f8939b9ea92f308.png) (5)
(5)
(5)中,
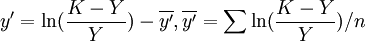 (6)
(6)
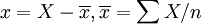 (7)
(7)
以為樣本容量。回歸參數a和b的樣本估計值為:
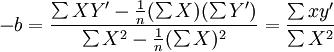 (8)
(8)
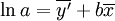 (9)
(9)
根據表2以及式(6)(7)求得:
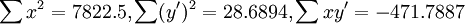
故根據(11)得: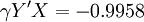 為極顯著.故知X和Y的關係以Logistic方程配合是合適的.進一步根據(6)和(7)求得b值為0.0603和a值為23.1316.那麼所求Logistic方程為:
為極顯著.故知X和Y的關係以Logistic方程配合是合適的.進一步根據(6)和(7)求得b值為0.0603和a值為23.1316.那麼所求Logistic方程為:
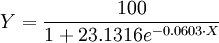
式(10)的曲線圖如圖所示
- 3.實驗和結果
採用的是CCERT的中文郵件樣本集,該樣本集由中國教育科研網收集並維護.該數據集在國內和教育網內是常用的一個衡量反中文垃圾郵件技術的數據集.採用數據集的8000封垃圾郵件以及8000封正常郵件.選擇貝葉斯方法進行垃圾郵件分類,分類結果利用查全率(Recall)、準確率(Precision)和F值評測過濾系統性能。
查全率(R)=正確過濾掉的郵件數/應該過濾掉的垃圾郵件數;
準確率(P)=正確過濾掉的郵件數/實際過濾掉的郵件數;
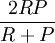 ;值實際是查全率和準確率的調和平均,綜合成一個指標.實驗結果如下表。
;值實際是查全率和準確率的調和平均,綜合成一個指標.實驗結果如下表。
表:統評測結果
| 信息熵 | 互信息 | 幾率比 | 期望交叉熵 | CHI統計量 | Logistic方程 | |
| Recall | 0.8446 | 0.8615 | 0.8954 | 0.8702 | 0.8737 | 0.9366 |
| Precision | 0.9698 | 0.9574 | 0.9421 | 0.9363 | 0.9316 | 0.9493 |
| F | 0.9028 | 0.9037 | 0.9181 | 0.9020 | 0.9017 | 0.9429 |
實驗結果表明,利用Logistic方程進行分類時的F值有顯著的提高,說明過濾系統整體性能有所提高,其中查全率有明顯的提高,說明這種方法檢出垃圾郵件的能力較高,使漏網的垃圾郵件減少,但是準確率沒有提升,說明合法郵件誤判為垃圾郵件的可能性沒有明顯降低。








謝謝你的講解,講解很詳細!