Kendall等級相關係數
出自 MBA智库百科(https://wiki.mbalib.com/)
| 本條目包含過多不是中文的內容，歡迎協助翻譯。 若已有相當內容譯為中文，可逕自去除本模板。 |
Kendall等級相關係數（Kendall tau rank correlation coefficient，肯德爾等級相關係數）
The Kendall tau rank correlation coefficient (or simply the Kendall tau coefficient, Kendall's τ or tau test(s)) is a non-parametric statistic used to measure the degree of correspondence between two rankings and assessing the significance of this correspondence. In other words, it measures the strength of Association of the cross tabulations.
It was developed by Maurice Kendall in 1938.
目錄 |
The Kendall tau coefficient (τ) has the following properties:
- If the agreement between the two rankings is perfect (i.e., the two rankings are the same) the coefficient has value 1.
- If the disagreement between the two rankings is perfect (i.e., one ranking is the reverse of the other) the coefficient has value −1.
- For all other arrangements the value lies between −1 and 1, and increasing values imply increasing agreement between the rankings. If the rankings are completely independent, the coefficient has value 0 on average.
Kendall tau coefficient is defined
where n is the number of items, and P is the sum, over all the items, of the number of items ranked after the given item by both rankings.
P can also be interpreted as the number of concordant pairs . The denominator in the definition of τ can be interpreted as the total number of pairs of items. So, a high value of P means that most pairs are concordant, indicating that the two rankings are consistent. Note that a tied pair is not regarded as concordant or discordant. If there is a large number of ties, the total number of pairs (in the denominator of the expression of τ) should be adjusted accordingly.
- Tau a — This tests the strength of association of the cross tabulations when both variables are measured at the ordinal level but makes no adjustment for ties.
- Tau b — This tests the strength of association of the cross tabulations when both variables are measured at the ordinal level. It makes adjustments for ties and is most suitable for square tables. Values range from −1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association.
- Tau c — This tests the strength of association of the cross tabulations when both variables are measured at the ordinal level. It makes adjustments for ties and is most suitable for rectangular tables. Values range from −1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association.
Suppose we rank a group of eight people by height and by weight where person A is tallest and third-heaviest, and so on:
| Person | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| Rank by Height | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Rank by Weight | 3 | 4 | 1 | 2 | 5 | 7 | 8 | 6 |
We see that there is some correlation between the two rankings but the correlation is far from perfect. We can use the Kendall tau coefficient to objectively measure the degree of correspondence.
Notice in the Weight ranking above that the first entry, 3, has seven other elements to its right (4,1,2,5,7,8,6). How many of these elements are also to the right of 3 in the other ranking?
The elements to the right of 3 in the Height ranking are: 4,5,6,7,8, so the number of elements to the right of 3 in both rankings is 5 (they are 4,5,6,7,8) and so the contribution to P of this entry is 5.
Moving to the second entry, 4, we see that there are six elements to the right of it. Among these elements those that are to the right of 4 also in the other ranking are four (5,6,7,8), so the contribution to P is 4. Continuing this way, we find that
- P = 5 + 4 + 5 + 4 + 3 + 1 + 0 + 0 = 22.
Thus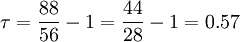 
. This result indicates a strong agreement between the rankings, as expected.
- (2007) Kendall rank correlation. In N.J. Salkind (Ed.): Encyclopedia of Measurement and Statistics. Thousand Oaks (CA): Sage.
- Kruskal, W.H. (1958) "Ordinal Measures of Association", Journal of the American Statistical Association, 53(284), 814-861.
- Kendall, M. (1948) Rank Correlation Methods, Charles Griffin & Company Limited
- Kendall, M. (1938) "A New Measure of Rank Correlation", Biometrika, 30, 81-89.
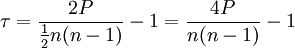
gei wo huy dian hua