高斯-博內定理

用手机看条目

什麼是高斯-博內定理

　　在微分幾何中，高斯-博內定理是指關於曲面的圖形（由曲率表徵）和拓撲（由歐拉示性數表徵）間聯繫的一項重要表述。它是以卡爾•弗里德里希•高斯和皮埃爾•奧西安•博內命名的，前者發現了定理的一個版本但從未發表，後者1848年發表了該定理的一個特例。

　　設 $M$ 是一個緊的二維黎曼流形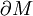， $\partial M$ 是其邊界。令 $K$ 為 $M$ 的高斯曲率， $k g$ 為 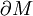$\partial M$ 的測地曲率。則有

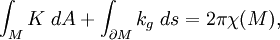
　　 $\int_M K\;dA+\int_{\partial M}k_g\;ds=2\pi\chi(M), \,$

　　其中dA是該曲面的面積元，ds是M邊界的線元。此處 $χ(M)$ 是 $M$ 的歐拉示性數。

　　如果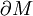 $\partial M$ 的邊界是分段光滑的，我們將 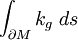$\int_{\partial M}k_g\;ds$ 視作光滑部分相應的積分之和，加上光滑部分在曲線邊界上的轉過的角度之和。

如果您認為本條目還有待完善，需要補充新內容或修改錯誤內容，請編輯條目或投訴舉報。

提示:評論內容為網友針對條目"高斯-博內定理"展開的討論，與本站觀點立場無關。

發表評論請文明上網，理性發言並遵守有關規定。