香農定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
香農定理是香農在信號處理和信息理論等相關領域的研究中．通過計算信號在經過一段距離如何衰減以及一個給定信號能載入多少數據之後．得到了一個公式：
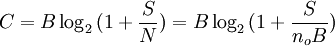
這個公式就是著名的香農定理。
其中：B為通道帶寬（Hz）；S為信號功率（W）；no為雜訊功率譜密度（W/Hz）；N為雜訊功率（W）。
由香農公式得到的重要結論：
（1）通道容量受三要素B、S、no的限制。
（3）若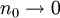
，則
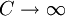，表明無雜訊通道的容量為無窮大。
（4）若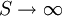
，則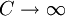，表明當信號功率不受限制時，通道容量為無窮大。
（5）C隨著B的適當增大而增大，但不能無限制的增大，即當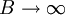
時，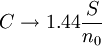
。
（6）C一定時，B與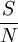
可以互換。
（7）若信源的信息速率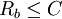
，則理論上可實現無誤差傳輸。[1]
香農定理在傳播學[2]
香農定理規定了有隨機熱雜訊通道的最大傳輸速率與通道帶寬、信號雜訊功率比之間的關係。從自然科學的角度看，香農定理用數學公式計量了信息（比特）的流量，具備典型的工程學意義。由於香農的科學家身份和研究的對象區域，香農定理與相關理論關心的不是信息表達的含意，而是信息的有效傳輸和接收。
香農在論文中區別了信息傳播的三個層次：A層：傳播符號如何能夠被準確地發射（技術問題）；B層：被髮射的符號如何能夠準確地傳遞意圖中的意義（語義學問題）；C層：被接受的意義如何有效地以意圖中的方式影響行為（效果或行為問題）。有趣的是：香農反覆聲明他所創立的信息理論只與A層打交道，並告誡學界不要過分廣泛地把這種理論用於所有類型的信息傳播理論的研究上。因為人與人之間的關係或人與社會之間的關係，遠比人與機器之間的關係或機器與機器之間的關係更為複雜。香農不願為之交道的B層和C層似乎更靠近以社會人文為基礎的傳播學理論。
後香農時代的英國傳播學者斯圖亞特·霍爾在1973年發表的《電視話語的編碼和解碼》一文中，對電視話語傳播的狀態和效果進行瞭解讀。電視話語意義在編碼過程中，電視話語的生產和流通分為三個階段：第一階段，媒介工作者對原材料進行加工，即進行電視話語“意義”的加工或創造，這個階段被霍爾稱為“編碼”階段。媒介工作者是受過專門訓練和經過專項學習的，他在進行編碼工作時，起作用的是他的世界觀、知識結構和專項技術的水準。霍爾認為，原材料中蘊含著文化代碼，這種代碼是自然的、中立的、約定俗成的它早已融入人們生活的社會結構之中，而編碼的過程就是媒介工作者在一定的文化視角下釋放代碼的意義。
第二個階段叫“成品”階段。電視作品完成後，代碼在編碼的過程中被註入了“意義”，這種意義構成了電視話語的主體，吸引受眾接受電視話語的中心由代碼（原材料）轉移到了編碼（解讀及產生的“意義”）上面。這裡面加入了人的因素。原材料（某種事物，某種生活現象或某種文化思想）散髮出的一種存在價值是自然的、中立的，甚至是約定俗成的，但企圖解讀並詮釋其中的“意義”時，就會產生各種視角和立場，但這些與接受電視話語意義的受眾無關。因此，電視的“成品”是“多義”的，而不是“多”的。當電視圖像話語將三維的世俗世界事物轉換成二維平面的電子信息之後，它自然就不可能成為它所指的對象或概念，它只是圖像符號。所以，電視話語只不過是對原材料的解讀，這種解讀不一定與事實相符，受眾完全可以從自己的視角、立場和認知水平來作為另行解讀的基礎。
第三個階段稱為“解碼”階段。解碼指電視受眾對電視作品中釋放出的話語意義的接受程度。接受則生成對電視作品的“消費”，產生認同感；不接受則沒完成對電視作品的“消費”，產生對立感或一定程度的爭議。從另一個角度觀察，假設被髮射的符號準確地傳遞了編碼者意圖中的意義，但該意義已經加入了編碼者主觀的判斷和觀點，即使機器和機器所發射的符號在技術上無懈可擊，依然存在編碼者意圖中的意義，進入大眾傳播領域後，被拒絕和修正的可能。在解碼過程中，即反映傳播效果或行為的過程中，傳播符號既然進入大眾人群，傳者與受者的互動便開始了。互動涉及到社會的各色人群，這些人群之間的關係、背景、素養等是需要分層的，分層決定了對符號傳播的話語意義不同的認識立場。由此，最小化的對立碼成了符號意義在傳播運動中是否被消費的標準。
可以認為的是：從香農定理到編碼與解碼理論，已經建立起了現代傳播學理論的框架和模型，並基本解決了信息在傳播過程中的定量和定性問題。但時過境遷，數字技術背景下顯現出來的信息傳播問題，已經在信息傳播的過程中極大地突破了現有傳播學理論的邊界，傳播學理論急切地需要新的內容。然而，香農定理對於通道帶寬的信息路徑、對於信息流量的控制計量依然散髮揮著物理技術的悠長魅力。
香農定理包括三大定理:可變長無失真信源編碼定理，有噪通道編碼定理，保真度準則下的信源編碼定理。
可變長無失真信源編碼定理[3]
1948年,美國工程師香農在貝爾實驗室雜誌上發表了長文《通訊的數學原理》。他用概率測度和數理統計的方法系統地討論了通信的基本問題 ,得出了幾個重要而帶有普遍意義的結論 ,並由此奠定了現代資訊理論的基礎。香農編碼理論揭示了在通信系統中 ,採用適當的編碼後能夠實現高效率和高可靠地傳輸信息的規律 ,並給出了相應的信源編碼定理和通道編碼定理。 從數學觀點看 ,這些定理是最優編碼的存在定理。 它們給出了編碼的性能極限 ,在理論上闡明瞭通信系統中各種因素的相互關係 ,為尋找最佳通信系統提供了重要的理論依據。
香農第一編碼定理 (變長無失真信源編碼定理 )是最優編碼的存在性定理 ,該定理指出了要做到無失真信源編碼 ,每個信源符號平均所需要的最少的碼元數 ,同時 ,該定理指出了最優碼的存在性。
有噪通道編碼定理[4]
通道編碼定理 (一般指通道正編碼定理 )是資訊理論中的一個最重要的定理之一。它給出了通道無差錯傳輸時碼率的上界。
定理(通道編碼的正編碼定理)如果 C是一個離散無記憶通道 的通道容量 ,那麼 C必是該離散無記憶通道序列的一個可達速率。
保真度準則下的信源編碼定理[5]
而保真度準則下的信源編碼定理，或稱有損信源編碼定理，只要碼長足夠長，總可以找到一種信源編碼，使編碼後的信息傳輸率略大於率失真函數，而碼的平均失真度不大於給定的允許失真度。
無線通信的實現勢必要解決兩大問題,其一是對信源進行高效的壓縮以充分利用有限的通道帶寬,即信源編碼問題；其二是對壓縮後的信息進行錯誤保護以抵禦通道或網路所帶來的誤碼或數據丟失,即通道編碼問題。信源編碼和通道編碼所要解決的問題在一定意義上是相互矛盾的：一方面,信源編碼壓縮率的提高將導致壓縮後的碼流抗誤碼能力的降低,另一方面,提高碼流的抗誤碼性能又要以犧牲壓縮效率為代價。
香農定理的意義[5]
香農在二十世紀四十年代初奠定了通信的數字理論基礎。同時香農三大定律是資訊理論的基礎，雖然沒有提出具體的編碼實現方法，但是為通信信息的研究指明瞭方向。他的“通道容量定理”指出，可以找到這樣一種技術，當數據傳輸速率不大於某個最大傳輸的速率時，通過它可以以任意小的錯誤概率傳輸信號。同時香農也給出了有雜訊通道的最大傳輸速率與寬頻的關係。
