顫抖手精煉均衡
出自 MBA智库百科(https://wiki.mbalib.com/)
顫抖手精煉均衡(trembling hand perfect equilibrium)
目錄 |
“顫抖手精煉均衡”概念是澤爾騰提出的對納什均衡的一個改進。顫抖手精煉均衡的基本思想是:在任何一個博弈中,每個局中人都有一定的犯錯誤的可能性(類似一個人用手抓東西時,手一顫抖,他就抓不住他想抓的東西)。一個策略對是一個顫抖手精煉均衡時,它必須具有如下性質:各局中人i要採用的策略,不僅在其他局中人不犯錯誤時是最優的,而且在其他局中人偶爾犯錯誤(概率很小,但大於0)時還是最優的。可以看出,顫抖手精煉均衡是一種較穩定的均衡。
從博弈論中我們知道,澤爾騰的這種“顫抖手均衡(trembling hand equilibrium)”也是一種精煉納什均衡。大致說來,澤爾騰(1975)假定,在博弈中存在一種數值極小但又不為0的概率,即在每個博弈者選擇對他來說所有可行的一項策略時,可能會偶爾出錯,這就是所謂的“顫抖之手”。因之,一個博弈者的均衡策略是在考慮到其對手可能“顫抖”(偶爾出錯)的情況下對其對手策略選擇所作的最好的策略回應。單從這一點來看,在演進博弈論中,最初的演進穩定性的出現,並不完全來自博弈雙方的理性計算,而實際上可能是隨機形成的(往往取決於博弈雙方“察言觀色”的一念之差)。按照這一分析思路,我們也可以認為,人們對一種習俗(演進穩定性)的偏離,也可能出自澤爾騰所說的那種人們社會博弈中的“顫抖”。
為了說明顫抖手精煉均衡的價值,我們考慮一個具有兩個“委托人—代理人”對和兩種自然狀態的對稱支付模型。設代理人1的策略有:α1(積極工作)和α2(偷懶);代理人2的策略同樣有β1(積極工作)和β2(偷懶)。相應於兩個代理人的策略,在自然狀態s1和s2下,每個委托人的收益如下:
| β1 | β2 |
| α1(c1,c2) | (d1,a2) |
| α2(a1,d2) | (b1,b2) |
| β1 | β2 |
| α1(d1,d2) | (e1,b2) |
| α2(b1,e2) | (c1,c2) |
其中,0<aj<bj<cj<dj<ej,j=1,2。這意味著當自然狀態“壞”時,每個代理人都必須採用積極”的策略才可能使自己的委托人得到中等以上的收益(即不小於cj);而當自然狀態“好”時,兩代理人都選“偷懶”也可使各自的委托人得到cj的收益。現在設代理人j(j=1,2)在他的委托人的利潤不小於cj單位時,都得到 Uj;否則所得為-M。假設代理人j選擇“積極”策略時,就沒有額外收益,而選擇“偷懶”時,可有li>0單位的額外收益。因此,代理人的收益,可用如下標準形的二人非零和博弈給出:
| α1 | β1 ( U1, U2) | β2 ( U1-M) |
| α2 | (-M, U2) | (-M,-M) |
| α1 | β1 ( U1, U2) | β2 ( U1,-M) |
| α2 | (-M, U2) | ( U1+l1, U2+l2) |
這樣,在好的環境s2中,代理人之間的博弈有2個納什均衡:(α1,β1)對應收益對( U1, U2)和(α2,β2)對應收益對( U1,+l1, U2+l2);而在壞的狀態s1中,代理人間的博弈只有一個非合作均衡(α1,β1)對應收益對( U1, U2)。觀察上述博弈,我們發現在狀態s2中,(α1,β1)更加有效率(使每個委托人的收益都較大),然而兩個代理人卻更喜歡均衡(α2,β2),因為這個均衡使他們的效用從( U1, U2)升至( U1,+l1, U2+l2)。但是,如果這兩個納什均衡中只有(α1,β1)是顫抖手精煉均衡,代理人就可能不再偏愛均衡(α2,β2)。
顫抖手精煉均衡的舉例[1]
下麵通過一個例子,分析如何應用“顫抖”對博弈的解(即Nash均衡)進行精煉。考察圖1中的博弈,其中圖1(b)為圖1(a)中博弈的戰略式描述。顯然,博弈存在兩個純戰略Nash均衡——(L1,R2)和(R1,L2)。
首先考察均衡(L1,R2)。假設參與人2選擇行動R2時發生顫抖,其顫抖 (
(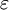 ,1-
,1-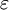 )(其中0<
)(其中0<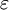 <1)。若0<
<1)。若0<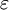 ≤1/2(即參與人2犯錯誤的可能性不大於1/2),則v1(L1,
≤1/2(即參與人2犯錯誤的可能性不大於1/2),則v1(L1, )≥v1(R1,
)≥v1(R1, )。假設參與人1選擇行動L1時發生顫抖,其顫抖
)。假設參與人1選擇行動L1時發生顫抖,其顫抖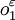 =(1一
=(1一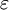 ,
,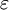 ),由於R2為參與人2的占優戰略,因此v2(R2,
),由於R2為參與人2的占優戰略,因此v2(R2,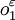 )≥v2(L2,
)≥v2(L2,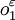 )。所以,(L1,R2)為顫抖手精煉均衡。同理可以證明(R1,L2)不是顫抖手精煉均衡。所以,對於圖1(b)所示的戰略式博弈,合理的均衡為(L1,R2),這與圖1(a)中“博弈的合理均衡為(L1,R2)”的結論相一致。
)。所以,(L1,R2)為顫抖手精煉均衡。同理可以證明(R1,L2)不是顫抖手精煉均衡。所以,對於圖1(b)所示的戰略式博弈,合理的均衡為(L1,R2),這與圖1(a)中“博弈的合理均衡為(L1,R2)”的結論相一致。
- ↑ 羅雲峰主編.博弈論教程.清華大學出版社,2007.9.









記得看過一個嚴格的定義: 在n人策略表達式的博弈G={S1,S2,...,Sn;u1,u2,...,u3}中我們說納什均衡(p1,p2,...,pn)構成一個顫抖手精煉均衡,如果對於每個局中人i,存在一個嚴格混合策略序列{p(im)},滿足下列條件: (1)對於每個i,lim(m→∞)p(im)=pi (2)對於每個i和每個m=1,2,...,pi是對策略組合{p(m1),...,p(m i-1),p(m i+1),...,p(m n)的最優反應,即pi∈arg max ui=(●,p(m,-i))