隱馬爾可夫模型
出自 MBA智库百科(https://wiki.mbalib.com/)
隱馬爾可夫模型(Hidden Markov Model,簡稱HMM)
目錄 |
隱馬爾可夫模型是統計模型,它用來描述一個含有隱含未知參數的馬爾可夫過程。其難點是從可觀察的參數中確定該過程的隱含參數。然後利用這些參數來作進一步的分析,例如模式識別。
在正常的馬爾可夫模型中,狀態對於觀察者來說是直接可見的。這樣狀態的轉換概率便是全部的參數。而在隱馬爾可夫模型中,狀態並不是直接可見的,但受狀態影響的某些變數則是可見的。每一個狀態在可能輸出的符號上都有一概率分佈。因此輸出符號的序列能夠透露出狀態序列的一些信息。
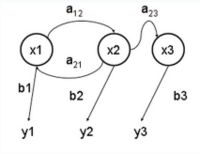
圖:隱馬爾可夫模型狀態變遷圖(例子)
x — 隱含狀態
y — 可觀察的輸出
a — 轉換概率(transition probabilities)
b — 輸出概率(output probabilities)]]
“隱馬爾可夫模型”最初是在二十世紀六十年代後半期Leonard E.Baum和其它一些作者在一系列的統計學論文中描述的。HMM最初的應用之一是開始於二十世紀七十年代中期的語音識別。
在二十世紀八十年代後半期,HMM開始應用到生物序列尤其是DNA的分析中。從那時開始,在生物信息學領域它們已經變得無處不在。
HMM有三個經典(canonical)問題:
- 已知模型參數,計算某一特定輸出序列的概率.通常使用forward演算法解決.
- 已知模型參數,尋找最可能的能產生某一特定輸出序列的隱含狀態的序列.通常使用Viterbi演算法解決.
- 已知輸出序列,尋找最可能的狀態轉移以及輸出概率.通常使用Baum-Welch演算法以及Reversed Viterbi演算法解決.
另外,最近的一些方法使用Junction tree演算法來解決這三個問題。
- 語音識別或光學字元識別
- 機器翻譯
- 生物信息學和基因組學
- 基因組序列中蛋白質編碼區域的預測
- 對於相互關聯的DNA或蛋白質族的建模
- 從基本結構中預測第二結構元素
具體實例
假設你有一個住得很遠的朋友,他每天跟你打電話告訴你他那天作了什麼.你的朋友僅僅對三種活動感興趣:公園散步,購物以及清理房間.他選擇做什麼事情只憑天氣.你對於他所住的地方的天氣情況並不瞭解,但是你知道總的趨勢.在他告訴你每天所做的事情基礎上,你想要猜測他所在地的天氣情況.
你認為天氣的運行就像一個馬爾可夫鏈. 其有兩個狀態 "雨"和"晴",但是你無法直接觀察它們,也就是說,它們對於你是隱藏的.每天,你的朋友有一定的概率進行下列活動:"散步", "購物", 或 "清理". 因為你朋友告訴你他的活動,所以這些活動就是你的觀察數據.這整個系統就是一個隱馬爾可夫模型HMM.
你知道這個地區的總的天氣趨勢,並且平時知道你朋友會做的事情.也就是說這個隱馬爾可夫模型的參數是已知的.你可以用程式語言(Python)寫下來:
states = ('Rainy', 'Sunny')
observations = ('walk', 'shop', 'clean')
start_probability = {'Rainy': 0.6, 'Sunny': 0.4}
transition_probability = {
'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},
'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},
}
emission_probability = {
'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},
'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},
}
在這些代碼中,start_probability代表了你對於你朋友第一次給你打電話時的天氣情況的不確定性(你知道的只是那個地方平均起來下雨多些).在這裡,這個特定的概率分佈並非平衡的,平衡概率應該接近(在給定變遷概率的情況下){'Rainy': 0.571, 'Sunny': 0.429}<
transition_probability 表示基於馬爾可夫鏈模型的天氣變遷,在這個例子中,如果今天下雨,那麼明天天晴的概率只有30%.代碼emission_probability 表示了你朋友每天作某件事的概率.如果下雨,有 50% 的概率他在清理房間;如果天晴,則有60%的概率他在外頭散步.








很棒的描述,謝謝