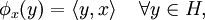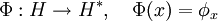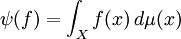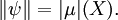裡斯表示定理

出自 MBA智库百科(https://wiki.mbalib.com/)

　　在泛函分析中有多個有名的定理冠以裡斯表示定理，它們是為了紀念匈牙利數學家弗里傑什•裡斯。

　　這個定理建立了希爾伯特空間與它的連續對偶空間的一個重要聯繫：如果底域是實數，兩者是等距同構；如果域是複數，兩者是等距反同構。如下所述，（反）同構是特別自然的。

　　設 H 是一個希爾伯特空間，令 H ^* 表示它的對偶空間，由從 H 到域 或 的所有連續線性泛函。如果 x 是 H 中一個元素，則函數 φ_x 定義為

　　是 H ^* 的一個元素，這裡 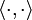表示希爾伯特空間的內積。裡斯表示定理斷言 H ^* 中任何元素都能惟一地寫成這種形式。

　　定理：映射

　　是一個等距（反）同構，這就是說：

• Φ 是雙射。
• x 的範數與 Φ(x) 的範數相等：。
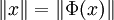• Φ 可加：Φ(x₁ + x₂) = Φ(x₁) + Φ(x₂)。
• 如果底域是 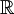，則 Φ(λx) = λΦ(x) 對所有實數 λ。
• 如果底域是 ，則 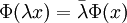對所有複數 λ，這裡 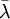表示 λ 的復共軛。

　　Φ 的逆映射可以描述為： 給定 H ^* 中一個元素 φ，核 φ 的正交補是 H 的一維子空間。取那個子空間中一個非零元素 z，令 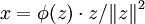。則 Φ(x) = φ。

　　歷史上，通常認為這個定理同時由弗里傑什•裡斯|裡斯和莫裡斯•雷內•弗雷歇在1907年發現（見參考文獻）。格雷在評論從他認為是原型的裡斯（1909）一文到裡斯表示定理的發展時說：“給定運算 A[f]，可以構造有界變差函數 α(x)，使得無論連續函數f(x) 是什麼，都有 ”

　　在量子力學的數學處理中，這個定理可以視為流行的狄拉克符號記法的根據。當定理成立時，每個右括弧 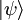有一個相應的左括弧 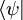，對應是清楚的。但是存在拓撲向量空間，比如核空間，裡斯表示定理不成立，在這樣的情形狄拉克符號變得不合適。

　　下麵的定理表示出 C_c(X) 上的正線性泛函，緊空間|緊支集連續函數 (拓撲學)|連續復值函數空間。下麵所說的波萊爾集表示由開集生成的 σ-代數。

　　局部緊豪斯多夫空間 X 上一個非負可數可加波萊爾測度 μ 是正規的當且僅當

• μ(K) < ∞ 對所有緊集 K；
• 對每個波萊爾集 E，

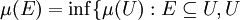開 }.

• 關係

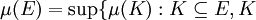閉 }.

成立只要 E 是開集和 E 是波萊爾集且 μ(E) < ∞。

　　定理：設 X 是一個局部緊豪斯多夫空間。對 C_c(X) 上任何正線性泛函 ψ，在 X 上存在惟一的波萊爾正則測度 μ 使得

對所有 f ∈ C_c(X)。

　　進入測度論的一個途徑是從拉東測度開始，定義為 C(X) 上一個正線性泛函。這種方式由布爾巴基採取；這裡顯然假設 X 首先是一個拓撲空間，而不僅是一個集合。對局部緊空間，重新得到了一個積分理論。

　　下麵定理也稱為裡斯-馬爾可夫定理，給出了 C₀(X) 的對偶空間的一個具體實現，X 上在無窮遠趨於零的連續函數。定理陳述中的波萊爾集合同樣指由開集生成的 σ-代數。結論與上一節類似，但不能包含在前一個結果之中。參見下麵的技術性註釋。

　　如果 μ 是一個復值可數可加波萊爾測度，μ 是正則的當且僅當非負可數可加測度 |μ| 正則（上一節所定義的）。

　　定理：設 X 是一個局部緊豪斯多夫空間。對 C₀ 上任何連續線性泛函 ψ，存在 X 上惟一正則可數可加波萊爾測度 μ 使得

對所有 f∈ C₀(X)。ψ 的範數作為線性泛函是 μ 的全變差（:en:total variation|total variation），即

　　最後，ψ 是正線性泛函|正的當且僅當測度 μ 是非負的。

　　註：C_c(X) 上任何有界線性泛函惟一延拓為 C₀(X) 上有界線性泛函，因為後一個空間是前者的閉包 (拓撲學)|閉包。但是 C_c(X) 上一個無界正線性泛函不能延拓為 C₀(X) 上一個有界線性泛函。因此前兩個結論應用的情形稍微不同。