菲波納契數列
出自 MBA智库百科(https://wiki.mbalib.com/)
菲波納契數列(Fibonacci Number)
目錄 |
菲波納契數列又稱“菲波納契神奇數列”,是由13世紀的義大利數學家菲波納契提出的,當時是和兔子的繁殖問題有關的,它是一個很重要的數學模型。這個問題是:有小兔一對,若第二個月它們成年,第三個月生下小兔一對,以後每月生產一對小兔,而所生小兔亦在第二個月成年,第三個月生產另一對小兔,以後亦每月生產小兔一對,假定每產一對小兔必為一雌一雄,且均無死亡,試問一年後共有小兔幾對?
對於n=1,2,……,令Fn表示第n個月開始時兔子的總對數,Bn、An分別是未成年和成年的兔子(簡稱小兔和大兔)的對數,則Fn = An + Bn。
根據題設,有:
| 月份n | 1 | 2 | 3 | 4 | 5 | 6 | …… | |
|---|---|---|---|---|---|---|---|---|
| A_n | 1 | 1 | 2 | 3 | 5 | 8 | …… | |
| B_n | 1 | 1 | 1 | 2 | 3 | 5 | …… | |
| F_n | 1 | 1 | 2 | 3 | 5 | 8 | 13 | …… |
顯然,F1 = 1,F2 = 1,而且從第三個月開始,每月的兔子總數恰好等於它前面兩個月的兔子總數之和,於是按此規律我們得到一個帶有初值的遞推關係式:
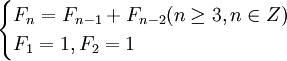
若我們規定F0 = 1,則上式可變為:
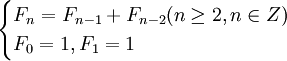
這就是Fibonacci數列的通常定義,也就是數列1、1、2、 3、5、8、13、 21、34、55、89、144、233、377、610、987、1597……,直至無限。這串數列的特點是:其中任一個數都是前兩數之和。從上述數字看,系列由1、2、3開始,繼而產生無限數字系列;這與《道德經》第四十二章:“道生一,一生二,二生三,三生萬物”所包含的道理不謀而合。由神奇數字演變出來的比率(即黃金比率,golden ratio),是 0.236、0.382、0.5、0.618、0.764、1.618、2.618 等,上述比率有助推斷未來高點或低點。
這個兔子問題是義大利數學家萊昂納多·菲波納契(Leonardo Fibonacci)在他所著的《算盤全集》中提出的,所以這個數列稱作菲波納契數列,其中每一項稱作Fibonacci數。
它的通項是![F_n = \frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n+1}-(\frac{1-\sqrt{5}}{2})^{n+1}]](/w/images/math/4/c/5/4c555d60df2e41fdb30dadad1e7344dc.png) ,由法國數學家比內(Binet)求出的。
,由法國數學家比內(Binet)求出的。
菲波納契數列既謂神奇數字,上述數字自有神奇之處,其特點包括:
1、從第三項起,任何一個數字均是其前兩個數字的和數,例如1+1=2;1+2=3;2+3=5;3+5=8;5+8=13;8+13=21;13+21=34等。
2、任何兩個相隔的數字彼此順序相除或倒轉相除,所得數字分別接近0.382及2.618。
接近0.382比率,例如:8÷21=0.381;13÷34=0.382;21÷55=0.382等。
接近2.618比率,例如:21÷8=2.625;34÷13=2.615;55÷21=2.619等。
3、除首四個數字(1、1、2、3)外,兩個相鄰數字彼此相除,所得數字分別接近0.618及1.618比率。
接近0.618比率,例如:5÷8=0.625;8÷13=0.615;13÷21=0.619等。
接近1.618比率,例如:8÷5=1.6;13÷8=1.625;21÷13=1.615等。
在股市中,菲波納契數列的作用在於預測未來走勢的升跌幅。若配合波浪理論,可以神奇數字計算出預期的升跌幅度;藉此,投資者可推測短線、中線或長線走勢的支持位或阻力位,及早趁低吸納或趁早沽出。








還好啊!