簡單季節指數法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
什麼是簡單季節指數法[1]
簡單季節指數法是指反映季節變化對銷售量影響的一種簡便方法。其實質就是計算各個季節的不同銷售指數。
簡單季節指數法的步驟[1]
簡單季節預測法的具體步驟如下:
1.收集歷年按季度記錄的歷史統計資料;
2.計算出n年各相同季度的平均值(A);
3.計算出n年每一個季度的平均值(月);
4.計算季節指數,即用各季度的平均值除以所有季度的平均值:
式中
C=A/B
C——季節指數。
5.利用季節指數(C),對預測值進行修正:
Yt = (a + bT)Ci
式中
Ci——第i季度的季節指數(i=1,2,3,4);
Yt——第t季度的銷售量;
a——待定繫數;
b——待定繫數;
T——預測期季度數,
簡單季節指數法實例分析[1]
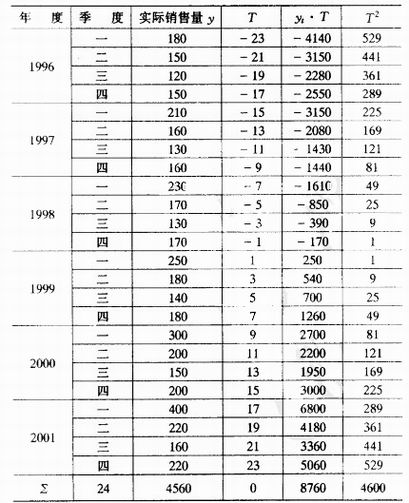
例如,某公司從1996年到2001年,每一年各季度的紡織品銷售量見下表。預測2002年各季度紡織品的銷售量。
| 年度 | 年度銷售量 | 第一季度 | 第二季度 | 第三季度 | 第四季度 |
| 1996 | 600 | 180 | 150 | 120 | 150 |
| 1997 | 660 | 210 | 160 | 130 | 160 |
| 1998 | 700 | 230 | 170 | 130 | 170 |
| 1999 | 750 | 250 | 180 | 140 | 180 |
| 2000 | 850 | 300 | 200 | 150 | 200 |
| 2001 | 1000 | 400 | 220 | 160 | 220 |
| 合計 | 4560 | 1570 | 1080 | 830 | 1080 |
| 季節指數 | 1.38 | 0.95 | 0.73 | 0.95 |
預測過程如下:
1.六年各相同季節的平均銷售量(Ai)
A1=1570÷6≈262(單位)
同理 A_2=180,A_3≈138.3,A_4=180(單位)
2.六年所有季度的平均銷售量(B)
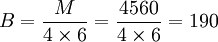 (單位)
(單位)
M——6年銷售量總和
3.各季節銷售指數(Ci)
Ci=262÷19≈1.38
同理 C2≈0.95,C3≈0.73,C4≈0.95
4.修正2002年各季度預測值
由上表可得知各有關數據,利用公式
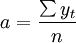 (1)
(1)
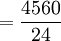
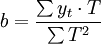 (2)
(2)
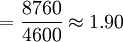
y_t=190+1.90T
式中 T=-23,-21,…,-1,1,3,…,23
(2)修正2002年各季度預測值
第一季度預測值=(190+1.90×25)×1.38≈328(單位)
第二季度預測值=(190+1.90×27)×0.95≈229(單位)
第三季度預測值=(190+1.90×29)×0.73≈179(單位)
第三季度預測值=(190+1.90×31)×0.95≈236(單位)
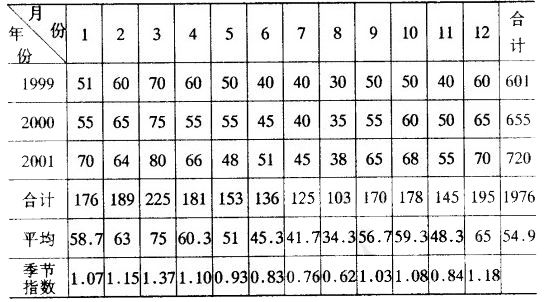
註意:如果n為奇數,例如n=9,則T=-4,-3,-2,1,0,1,2,3,4.季節銷售指數也可以按月計算。先列出各個年度每個月份的銷售量,見下表。計算過程如下:
A=各月合計值÷年數
A1=176/3\approx58.7(單位)
A2 = 189 / 3 = 63(單位)
vdots
A12 = 195 / 3 = 65(單位)
2.計算所有月份的月平均值銷售量(B)
B=所有月份的合計值÷年數÷12
B=1976÷3÷12≈54.9(單位)
3.求各月份季節銷售指數(C)
Ci = A / B
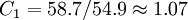
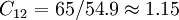
vdots
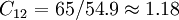
在本例中,a=54.9,b=0.13,由公式(1)(2)
得
yt = (54.9 + 0.13T)Ci
(預測模型建立過程從略)若預測2002年1月份和8月份的銷售量,計算如下:
2002年1月和8月份的銷售額分別為
y19=(54.9+0.13×37)×1.07≈63.89
y26=(54.9+0.13×51)×0.62≈38.15
註;(這裡的順序37和5l是用表2中的排序法得到的)。








公式中的a,b,計算步驟,可否更詳細一點?