威爾科克森符號秩檢驗
出自 MBA智库百科(https://wiki.mbalib.com/)
威爾科克森符號秩檢驗（Wilcoxon's Sign Rank Test）
目錄 |
什麼是威爾科克森符號秩檢驗[1]
威爾科克森符號秩檢驗是由威爾科克森（F·Wilcoxon）於1945年提出的。該方法是在成對觀測數據的符號檢驗基礎上發展起來的，比傳統的單獨用正負號的檢驗更加有效。它適用於T檢驗中的成對比較，但並不要求成對數據之差di服從正態分佈，只要求對稱分佈即可。檢驗成對觀測數據之差是否來自均值為0的總體（產生數據的總體是否具有相同的均值）。
威爾科克森符號秩檢驗的步驟[1]
正負符號檢驗和威爾科克森符號秩檢驗，都可看作是就成對觀察值而進行的參數方式的T檢驗的代用品，非參數檢驗具有無需對總體分佈作假定的優點，而就成對觀察值作的參數方式的T檢驗，必須假定有關的差別總體服從正態分佈。
該方法具體步驟如下：
第一步：求出成對觀測數據的差di，並將di的絕對值按大小順序編上等級（曼-惠特尼U檢驗）。
第二步：等級編號完成以後恢復正負號，分別求出正等級之和T+和負等級之和T-，選擇T+和T-中較小的一個作為威爾科克森檢驗統計量T。
第三步；作出判斷。
根據顯著性水平α查附表，得到臨界值Tα，若T＜Tα，則拒絕原假設H0。當觀測值不少於20對時，統計量T的均值和方差分別為：
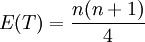
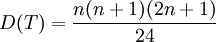(n為成對觀測的個數)
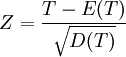(近似服從標準正態分佈)
若Z＜-Zα(單側)或Z＜-Zα/2(雙側)，則拒絕H0。
威爾科克森符號秩檢驗的應用舉例[1]
下麵是分別用高錳酸鉀法和EDTA法對某生長期蛋雞配合料鈣含量進行的7次測定結果(湖北省飼料質量監督檢驗站2002年常規檢測樣品)，比較兩種方法測定結果差異是否顯著。
首先按大小順序對兩對觀測值之差di進行等級排序，並加上正負號，分別計算正負等級之和：T+=21，T-=-7。
高錳酸鉀法和EDTA法測定蛋雞配合料鈣含量結果(%)
| 編號 | 高錳酸鉀法 | EDTA法 | di | 等級 |
|---|---|---|---|---|
| 1 | 1.26 | 1.24 | 0.02 | 4.5 |
| 2 | 1.24 | 1.28 | -0.04 | -7 |
| 3 | 1.24 | 1.21 | 0.03 | 6 |
| 4 | 1.25 | 1.25 | 0 | 1.5 |
| 5 | 1.26 | 1.26 | 0 | 1.5 |
| 6 | 1.25 | 1.24 | 0.01 | 3 |
| 7 | 1.24 | 1.22 | 0.02 | 4.5 |
(註)編號4 和5 應該 為等級1和2,因為 di相同,所以(1+2)/2 ,分別為1.5. 編號1和7同理
假設兩種方法檢測飼料中鈣含量結果無顯著差異，即檢驗：
- H0：兩種方法檢測結果無顯著差異；
- H1：兩種方法檢測結果有差異。
查附表得到，對於α=0.05的雙側檢驗，n=7 時，T0.025=2。由於 T+=21＞ T0.025 ，則接受H0，可以認為兩種方法測定飼料鈣含量結果並無顯著差異。
附表
威爾科克森帶符號秩檢驗T的臨界值表
| 單側α | 雙側α | n值 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.10 | T值 | 1 | 2 | 4 | 6 | 8 | 11 | 14 | 17 | 21 | 26 | 30 | 36 |
| 0.025 | 0.05 | 1 | 2 | 4 | 6 | 8 | 11 | 14 | 17 | 21 | 25 | 30 | ||
| 0.01 | 0.02 | 0 | 2 | 3 | 5 | 7 | 10 | 13 | 16 | 20 | 24 | |||
| 0.005 | 0.01 | 0 | 2 | 3 | 5 | 7 | 10 | 13 | 16 | 19 |
例子是錯的