交叉影響法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
交叉影響法,也即交叉概率法，是美國於上世紀60年代，在德爾菲法和主觀概率法基礎上發展起來的一種新的預測方法。這種方法是主觀估計每種新事物在未來出現的概率，以及新事物之間相互影響的概率，對事物發展前景進行預測的方法。
交叉影響法就是研究一系列事件Dj(D1，D2...,Dn)及其概率Pj(P1，P2...,Pn)之間相互關係的方法,其方法步驟下：
(1)確定其他事件對某一事件的影響關係
(2)專家調查，評定影響程度。
(3)計算變化概率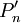
並得出分析結果。
(4)用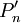代替Pn進行風險決策。
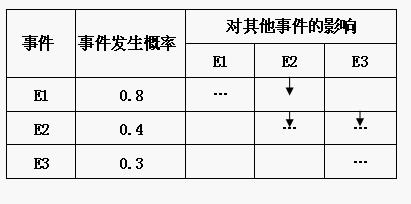
1.估計一組預測事件的概率，確定交叉影響方向矩陣。
例：某國在考慮今後15年的能源政策時，列出三種可能的能源政策。如下表:
2.確定交叉影響的程度
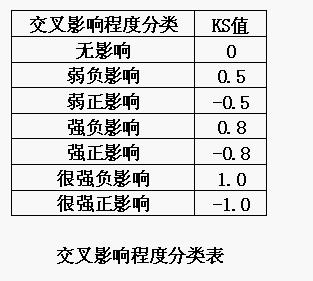
S代表交叉影響的程度，其變動範圍在0與1之間，分為無、弱、強、很強四級，K代表一事件與另一事件的上升或下降關係。k=-1表示上升聯繫；K=+1表示下降聯繫。將KS結合，交叉影響程度分類如下：
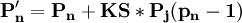
請專家參照上表打分，可得到上例的實際交叉影響KS值矩陣(見下表)。
3.計算校正概率
每一事件的校正概率計算過程如下：如從D1、D2、D3事件中隨機抽取的事件時D3。
①用隨機數法確定事件D_3是否發生，即從0-99的隨機數字表中隨機抽取一數(假如是55)，與已抽取的事件D3的初始概率P3相比較，由於55>30，故D3事件不發生；如果抽取的是25，由於25<30則D3事件將發生。
②如果隨機抽取的事件不發生，將不影響其餘事件，則其餘事件的初始概率均不變。如果隨機抽取的事件發生，將影響其餘事件，受其影響的其餘事件的概率均應按照上表中的數據，利用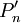公式計算校正概率。
③對第①步未抽中的其餘事件，均要經過①和②步。
④上述過程反覆進行，直到n個事件是否發生都經過檢驗為止，再恢復到初始概率，併進入第⑤步。
⑤重做①至④反覆多次。
交叉影響法應用於風險決策的效果分析
(1)交叉影響法抓住了風險決策中最關鍵的問題,即自然狀態出現的概率問題。
(2)由於概率的變化可以充分辨明影響方向，給決策者指明瞭明確的決策方向，使決策目標更為清楚。
(3)自然狀態變化的概率趨於準確，雖然變化後的狀態概率仍屬不完全信息，但大大地減少了不確定性。因為計算出來的變化後的自然狀態出現的概率是多數專家的意見．加之取各位專家的平均值，使之變化後的自然狀態概率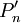更趨於準確。在某種意義上說平均值趨於真值，尤其是樣本個數無窮多的時候，平均值可認為真值。
(4)交叉影響法應用於風險決策，對決策問題的影響事件做了全面的考慮。既考慮了正面影響，又考慮了負面影響，是一種綜合分析問題的思想方法,避免了片面性，減步了決策失誤。
通過分折可以看出。交叉影響法完全可以用於風險決策，可降低決策風險，可為決策者參考應用。
1.優點：
①能考慮事件之間的相互影響及其程度和方向；
②能把有大量可能結果的數據，有系統地整理成易於分析的形式。
2.缺點：
①根據主觀判斷的數據，利用公式將初始概率轉變成校正概率，有相當的主觀任意性。
②交叉影響因素的定義還須更加明確、具體、更加嚴格地確定。
1.估計一組預測事件的概率，確定交叉影響方向矩陣。
例：某國在考慮今後15年的能源政策時，列出三種可能的能源政策。
2.確定交叉影響的程度
S代表交叉影響的程度，其變動範圍在0與1之間，分為無、弱、強、很強四級，K代表一事件與另一事件的上升或下降關係。k=-1表示上升聯繫；K=+1表示下降聯繫。將KS結合，交叉影響程度分類
請專家參照上表打分，可得到上例的實際交叉影響KS值矩陣。 3.計算校正概率 每一事件的校正概率計算過程如下：如從D1、D2、D3事件中隨機抽取的事件時D3。
①用隨機數法確定事件D_3是否發生，即從0-99的隨機數字表中隨機抽取一數(假如是55)，與已抽取的事件D3的初始概率P3相比較，由於55>30，故D3事件不發生；如果抽取的是25，由於25<30則D3事件將發生。
②如果隨機抽取的事件不發生，將不影響其餘事件，則其餘事件的初始概率均不變。如果隨機抽取的事件發生，將影響其餘事件，受其影響的其餘事件的概率均應按照上表中的數據，利用公式計算校正概率。
③對第①步未抽中的其餘事件，均要經過①和②步。
④上述過程反覆進行，直到n個事件是否發生都經過檢驗為止，再恢復到初始概率，併進入第⑤步。
⑤重做①至④反覆多次。
