海盜博弈
出自 MBA智库百科(https://wiki.mbalib.com/)
海盜博弈(Pirate game)
目錄 |
海盜博弈是一個簡單的數學博弈。該博弈描述瞭如果遵循經濟人的行為,結果可能讓人驚訝。這同時也是最後通牒博弈的多參與者版本
海盜博弈故事[1]
有五個非常聰明的理性的海盜,分別編號P1,P2,P3,P4,P5。他們一同搶奪了100個金幣,現在需要想辦法分配這些金幣。 海盜們有嚴格的等級制度:P1 < P2 < P3 < P4 < P5。 海盜們分配原則是:等級最高的海盜P5提出一種分配方案。然後所有的海盜投票決定是否接受分配,包括提議人。並且在票數相同的情況下,提議人有決定權。如果提議通過,那麼海盜們按照提議分配金幣。如果沒有通過,那麼提議人將被扔出船外,然後由下一個最高等級的海盜提出新的分配方案。
海盜們基於三個因素來做決定。首先,要能存活下來。其次,自己的利益最大化(即得到最多的金幣)。最後,在所有其他條件相同的情況下,優先選擇把別人扔出船外。
現在,假如你是等級最高的P5,你會做何選擇?直覺上,為了保住自己的生命,你可能會選擇留給自己很少的金幣,以便讓大家同意自己的決策。然而,這和理論結果相差甚遠。
解決這個問題的關鍵是換個思維方向。與其苦思冥想你要做什麼決策,不如先想想最後剩下的人會做什麼決策。假設現在只剩下P1和P2了,P2會做什麼決策?很明顯,他將把100金幣留給自己,然後投自己一票。由於在票數相同的情況下提議人有決定權,無論P1同不同意,P2都將實現自己的目的。
現在再把P3加進來。P1知道,如果P3被扔下海,那麼游戲又將進行到上面的情況,P1終將一無所有。P3同樣看到了這一點,所以他知道,只要他給P1一點點利益,P1就會投票支持他的決策。所以P3最終的決策應該是: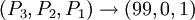
P4的策略也類似。由於他需要50%的支持,所以他只需賄賂1個金幣給P2就可以了。P2一定會支持他(否則輪到P3做決策,他就一無所有啦)。所以P4最終的決策是: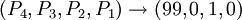
P5的情況稍有不同。由於這次一共有5個人,所以他至少需要賄賂兩個海盜以使自己的決議通過。所以唯一的決策就是: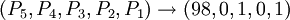
海盜博弈的延伸[1]
如果海盜的數目不止5個呢? 繼續按照這個邏輯推理,P6的決策將是: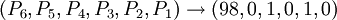 …一直到P200,它會給自己留1個金幣,同時給剩下所有偶數編號的海盜1個金幣。
…一直到P200,它會給自己留1個金幣,同時給剩下所有偶數編號的海盜1個金幣。
| 海盜 | P1 | P2 | P3 | P4 | P5 | … | P197 | P198 | P199 | P200 | |
| 決策者 | |||||||||||
| P1 | 100 | ||||||||||
| P2 | 0 | 100 | |||||||||
| P3 | 1 | 0 | 99 | ||||||||
| P4 | 0 | 1 | 0 | 99 | |||||||
| P5 | 1 | 0 | 1 | 0 | 98 | ||||||
| … | … | … | … | … | … | … | |||||
| P198 | 0 | 1 | 0 | 1 | 0 | … | 0 | 2 | |||
| P199 | 1 | 0 | 1 | 0 | 1 | … | 1 | 0 | 1 | ||
| P200 | 0 | 1 | 0 | 1 | 0 | … | 0 | 1 | 0 | 1 |
如果海盜數是201個,那麼P201該怎麼做呢?乍一看去,他好像沒有足夠的錢去賄賂別的海盜了。不過,為了保住自己的性命,他還是可以把自己手中的金幣全分出去,即給每個奇數編號的海盜(P1~P199)一個金幣。這樣雖然空手而歸,但不至於人財兩空。
P202也只能把這100個金幣全部賄賂給其他100個海盜,這100個海盜必須是在P201做決策的情況下什麼也得不到的海盜。由於符合這樣條件的海盜有101個(所有偶數編號的海盜P201),P202的決策不再是唯一的了!有101種方案供他選擇。
可憐的是P203。由於人數眾多,他實在沒有足夠的錢去賄賂其他海盜以獲得足夠的支持(他需要至少102個人的支持,包括他自己)。所以,不論P203做什麼決策,他都難逃被扔出船外的厄運了。不過P203並沒有我們想象中的那麼悲情,因為這樣的悲劇發生當且僅當船上正好有203個海盜。我們再增加一個海盜,P204。P204明白,P203現在的唯一願望就是活下來…所以不論P204做什麼決策,P203都會舉雙手支持他(當然舉多少手都只能算一票)。所以P204可以靠他自己的一票,P203的一票和賄賂另外100個海盜獲得正好50%的支持。
P204可能的決策也只有101種,如下表:(可能獲得1金幣的海盜用"Y"標示)
| P1 | P2 | P3 | P4 | … | P199 | P200 | P201 | P202 | P203 | P204 | |
| P204 | Y | N | Y | N | Y | N | N | Y | N | N |
P205就沒有那麼幸運了。他不能無償的得到P203和P204的支持。所以如果輪到P205做決策,他也必定被扔到船外。P206也一樣,儘管他能得到P205的免費支持,但是這還不夠。P207需要得到至少104個海盜的支持,所以有了P205,P206的無償支持還是不夠。
P208就比較幸運了。他也是需要得到104個海盜的支持,但P205,P206,P207,加上他自己,再加上賄賂100個海盜,正好104票。
P208可能的決策:(這次他有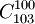 種決策)
種決策)
| P1 | P2 | P3 | P4 | … | P199 | P200 | P201 | P202 | P203 | P204 | P205 | P206 | P207 | P208 | |
| P208 | N | Y | N | Y | N | Y | Y | N | Y | Y | N | N | N | N |
從這裡我們又看出了新的規律:
從P201之後,在每兩個能夠作出決策保住自己生命的海盜之間,存在著一些無論如何決策都會被扔到船外的海盜。而這些海盜會支持在這之後的那個能夠做出決策保住自己生命的海盜。用數學來表達,設在P201之後,能夠作出決策保住自己生命的海盜的編號所組成的序列為an。則有:
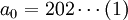
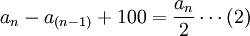
對於(2),
若an是偶數,則an = 2a(n − 1) − 200
若an是奇數,則an = 2a(n − 1) − 199
給定一個固定的初值,數列的下一項有兩個可能解:一個奇數解、一個偶數解,且偶數解比奇數解小1。再考慮我們原問題的意義,到達偶數解時,偶數編號的海盜已經能夠做出決策保全自己。這說明我們應該捨棄所有奇數解。
由an = 2a(n − 1) − 200以及a0 = 202,我們得到通解為:an = 200 + 2n + 1。考慮到P201也能保全自己,我們可以把所有能夠保全自己但卻得不到金幣的海盜的編號寫成統一表達式:
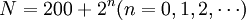
不難推出這些海盜可能的決策種數為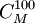 ,其中
,其中
- ↑ 1.0 1.1 邏輯與直覺–海盜博弈
評論(共29條)
海盜Pn只有在前n-1個海盜都扔到海裡的情況下才會成立,所以最後一個海盜就算沒有錢分,也一定是活著的,怎麼會被扔下水呢?
最後一個海盜P5不同意P4的觀點不會被丟到海裡,所以上述條件不成立,下麵一大堆推理前提不成立
回樓上 只有提議人會被仍進海裡的
問題是 到 p208時 不應該只有103選11的組合 應該是204選100的組合吧 【我電腦打不出 排列組合 C】 因為205,206,207和自己的四票是固定的 然而 對於前204個人來說 即使給204分 最多也只能得到1個金幣 此時 沒有必要再分 要給哪個人了吧。。。 或者說 當只能把100金幣全部分給其他人時 他的 下一個分配者就不必再思考 應該分給哪些特定的組合了吧。。。。應該是這樣 編者說呢。。
放在國內肯定不行 因為中國人不夠聰明而且貪婪
你聰明你上








太強了,理工科都暈