柯西中值定理

出自 MBA智库百科(https://wiki.mbalib.com/)

　　柯西中值定理是拉格朗日中值定理的推廣，是微分學的基本定理之一。其幾何意義為，用參數方程表示的曲線上至少有一點，它的切線平行於兩端點所在的弦。該定理可以視作在參數方程下拉格朗日中值定理的表達形式。

　　柯西中值定理粗略地表明，對於兩個端點之間的給定平面弧，至少有一個點，使曲線在該點的切線平行於兩端點所在的弦。

　　如果函數 f(x) 及 g(x) 滿足

　　在閉區間 [a,b] 上連續；

　　在開區間 (a,b) 內可導，

　　對任意 ，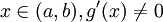

　　那麼在 (a,b) 內至少有一點 ξ(a < ξ < b) 使等式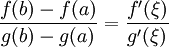成立。

　　其幾何意義為：用參數方程表示的曲線上至少有一點，它的切線平行於兩端點所在的弦。

　　首先，如果 g(a) = g(b)，由羅爾定理，存在一點 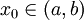使得 g'(x₀) = 0，與條件3矛盾。所以 。

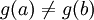　　令 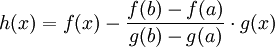。那麼

　　 h 在 [a,b] 上連續，

　　 h 在 (a,b) 上可導，

　　 。

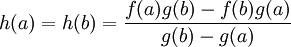　　由羅爾定理，存在一點 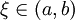使得 h'(ξ) = 0。即 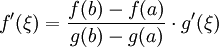。命題得證。