柯西中值定理

出自 MBA智库百科(https://wiki.mbalib.com/)

　　柯西中值定理是拉格朗日中值定理的推广，是微分学的基本定理之一。其几何意义为，用参数方程表示的曲线上至少有一点，它的切线平行于两端点所在的弦。该定理可以视作在参数方程下拉格朗日中值定理的表达形式。

　　柯西中值定理粗略地表明，对于两个端点之间的给定平面弧，至少有一个点，使曲线在该点的切线平行于两端点所在的弦。

　　如果函数 f(x) 及 g(x) 满足

　　在闭区间 [a,b] 上连续；

　　在开区间 (a,b) 内可导，

　　对任意 ，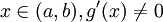

　　那么在 (a,b) 内至少有一点 ξ(a < ξ < b) 使等式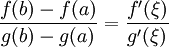成立。

　　其几何意义为：用参数方程表示的曲线上至少有一点，它的切线平行于两端点所在的弦。

　　首先，如果 g(a) = g(b)，由罗尔定理，存在一点 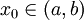使得 g'(x₀) = 0，与条件3矛盾。所以 。

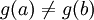　　令 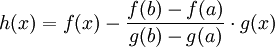。那么

　　 h 在 [a,b] 上连续，

　　 h 在 (a,b) 上可导，

　　 。

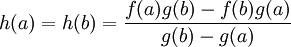　　由罗尔定理，存在一点 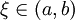使得 h'(ξ) = 0。即 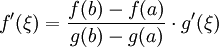。命题得证。