杠桿疊加原理

出自 MBA智库百科(https://wiki.mbalib.com/)

　　杠桿疊加原理是Zhangge根據道氏理論及BillWilliams的相關理論，取其精髓經過疊加併進行有效地量化而成。簡單的一句話概括如下：當價位有效突破一條相對較長期的趨勢線，且形成張氏分形時，之後的價位運行空間將是張氏分形中K線實體的至少1倍。杠桿是指壓力線的有效破位；疊加是指價位未來預期的運行空間。

　　根據“杠桿疊加原理”的描述——當價位有效突破一條相對較長期的趨勢線，且形成“張氏分形”時，之後的價位運行空間將是“張氏分形”中K線實體的至少1倍。

　　杠桿疊加原理的計算方法：

　　(1)在向上的張氏分形中，當滿足杠桿疊加原理以後，目標價位Cn點的計算方法為：

　　Cn=a的開盤價-(b的收盤價-a的開盤價)×100%

　　註：公式中門為l時，表示第一目標價位；n為2時，則為第二目標價位；以此類推。其中(b的收盤價-a的開盤價)為a與b之間的K線實體。“杠桿疊加原理”中所說的“疊加”二字就是在a的開盤價上向上加上a與b之間的K線實體，所加的數量至少是1個實體的距離，也可以是n個。由於這種增加像是建築中的一層一層的疊加，因此取“疊加”二字，用來形象地描述杠桿疊加原理中未來價位的運行空間。

　　例一：當n為1時。

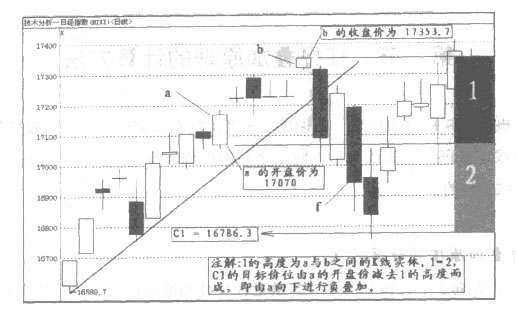
　　如下圖示例：(日經指數天圖2006-12-05至2007-01-23)

　　圖中a的開盤價=17070；(2006-12-26)

　　b的收盤價=17353.7；(2007-01-04)

　　C_1=17070-(17353.7-17070)×1=17070+283.7=16786.3

　　例二：當n為2時。

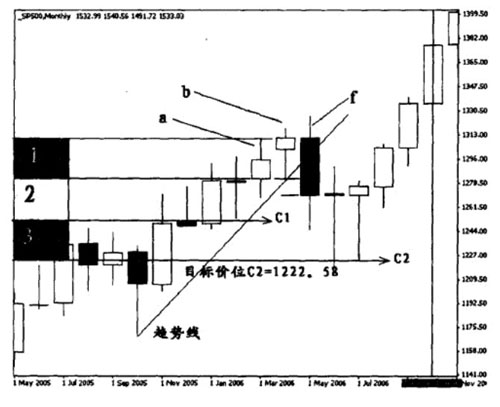
　　如下圖示例：(SP500月圖2005-05至2006-11)

　　圖中a的開盤價=1281.4；(2006-03)

　　b的收盤價=1310.81；(2006-04)

　　C1=1281.4-(1310.81-1281.4)×1=1281.4-29.4l=1251.99

　　C2=1281.4-(1310.81-1281.4)×2=1281.4-29.41×2=1222.58

　　(2)在向下的張氏分形中，當滿足杠桿疊加原理以後，目標價位Cn點的計算方法為：

　　Cn=a的開盤價+(a的開盤價-b的收盤價)×n

　　註：公式中n為1時，表示第一目標價位；n為2時，則為第二目標價位；以此類推。其中(a的開盤價-b的收盤價)為a與b之間的K線實體。

　　例一：當n為l時。

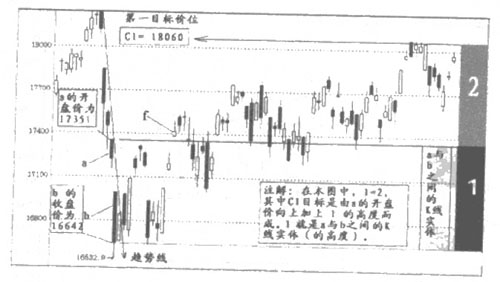
　　如下圖示例：(日經指數圖2007-02-14至2007-06-15)

　　圖中a的開盤價=17351；(2007-3-2)

　　b的收盤價=16642；(2007-3-5)

　　C1=17351+(17351—16642)×l=17351+709=18060

　　註：當n為2，為3，為4甚至更多時，計算方法類似。

　　1.進場點的選擇

　　當市場的走勢形態滿足杠桿疊加原理以後，可以有至少3種方法選擇進場點。

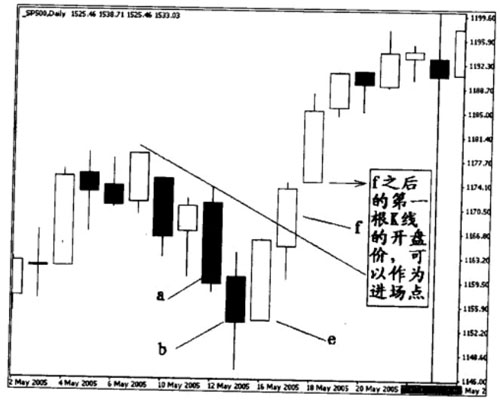
　　(1)如果滿足杠桿疊加原理時，張氏分形是以基本形態出現，大多情況下可以直接在f之後的第一根K線的開盤價入場。其原因是由於基本形態的走勢明瞭、簡單，反轉或調整的力度較大，一般不會給交易者太多的思考時間，是“杠桿疊加原理”中較好的進場選擇點。如下圖所示。

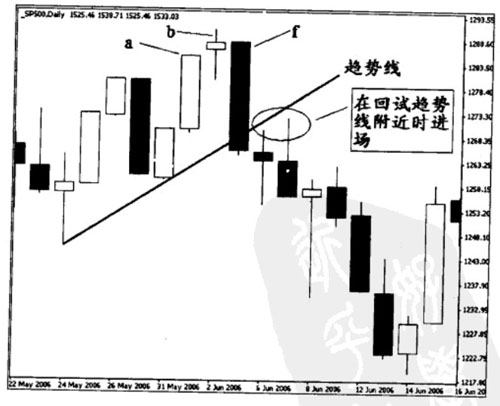
　　(2)在回試趨勢線附近時進場。當K線f的收盤價收在趨勢線之外，且同時滿足杠桿疊加原理時，未來的趨勢雖然已經明顯可見，但短期的價位運行大多會回試趨勢線附近，進行一次類似“告別”式的確認，此種點位的出現恰巧給交易者提供一個較好的入場點。如下圖所示。

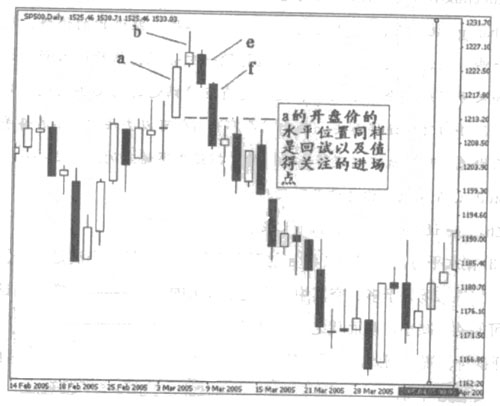
　　(3)在水平方向，回試K線a的開盤價附近時進場。當滿足杠桿疊加原理時，如果市場處於多、空其中一方處於較大的優勢時，B情形中回試趨勢線的可能就會減小，取而代之的是僅僅回試水平方向的強支撐位置——K線a的開盤價位置。因此，K線a的開盤點位應該也是一個值得密切關註的進場點。如下圖。

　　2.止損點的選擇

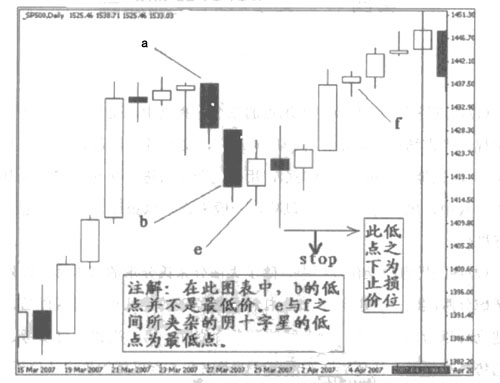
　　(1)在向上的張氏分形中，止損點放置在張氏分形中的最高點之上。

　　(2)在向下的張氏分形中，止損點放置在張氏分形中的最低點之下。

　　一般情況下，b經常出現最高或最低點，但前面曾經講過，張氏分形的極限點位經常是不固定的，因此交易者在此問題上要多加留意，如下圖所示。

　　3.出場點的選擇

　　當市場按預期運行到Cn點時，可以考慮部分獲利了結平倉。然後把止贏單設置在進場點以外或Cn-1位置，並繼續觀望或重新對市場進行分析及制定出新的操作策略。