多屬性決策
出自 MBA智库百科(https://wiki.mbalib.com/)
多屬性決策(Multiple Attribute Decision Making,MADM)
目錄 |
多屬性決策也稱有限方案多目標決策,是指在考慮多個屬性的情況下,選擇最優備選方案或進行方案排序的決策問題,它是現代決策科學的一個重要組成部分。它的理論和方法在工程、技術、經濟、管理和軍事等諸多領域中都有廣泛的應用。
多屬性決策主要解決的問題是在評估及選擇二方面[1]。
多屬性決策的共通要素[1]
如今被髮展的多屬性決策方法有很多,但這些方法有一些共通要素[2]:
1、多個選擇方案:在做群體決策之前,決策者必須先要衡量可行的方案數,以做為評估的選擇。
2、多個評估屬性:在做群體決策之前,決策者必須先要衡量可行的屬性數,提出影響方案的數個相關屬性,屬性間可以是互相獨立也可以是有相關聯。
3、屬性的權重分配:對於不同的屬性決策者會有不同的偏好傾向,分配不同的權重給不同的屬性,一般來說屬性的權重分配通常會經過正規化處理。
多屬性決策的方法[1]
如今所發展出的多屬性決策方法有很多,而Lahdelma[3]將其所運用的決策模型分為二類:第一類是以價值或效用函數為基礎的方法。第二數是以優勢排序為基礎的方法。
下麵是多屬性決策的一些方法,如ELECTRE法,層級分析程式法(AHP),多屬性價值理論法(MAVT),TOPSIS法。
1、ELECTRE法
ELECTRE(Elimination et choix traduisant laréalité)法[2]首先1966年被Benayoun等人提出,ELECTRE 最主要的概念是去處理方案和方案間使用準則做為評估的超越關係(“out ranking relationship”) 。及建立方案和方案間的優勢關係以淘汰較差的方案。若超越關係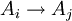 ,即方案i優於方案j。
,即方案i優於方案j。
2、AHP法
層級分析程式法(Analytic Hierarchy Process,AHP)[2]為Thomas L.Saaty在1971年所提出,主要是在處理有關不確定情形及數個屬性評估準則的問題上,提供階層的概念,將問題的結構可分為由上至下幾層,可使問題更有可讀性,並且在相對的屬性準則評估之間,採用了成對比較,建立成對比較矩陣,並求出其特征向量,其特征向量代表個方案間屬性準則之間的比重,藉由得到各層屬性準則之間的比重之後,便可算出最終方案的優劣順序。
3、MAVT法
多屬性價值理論(Multi-Attribute Value Theory,MAVT)主要是讓決策者可以對每個不同的屬性準則提供不同的屬性價值函數(attribute valuefunction)[4],結合每個屬性價值函數再經過權重總合計算後,便得到每個方案的效用值。
4、TOPSIS法
TOPSIS是由Hwang and Yoon所發展出來的一種多屬性決策方法[5]。仍是採用與正理想解之相對接近值的方法來進行方案的排序,在選擇方案時以距離正理想解最近,而距離負理想解最遠的方案為最佳方案,而距離的計算則是以歐幾里德幾何距離為計算依據。所謂正理想解是各可行方案利益面屬性值最大者,成本面屬性值最小者;反之,負理想解是各可行方案利益屬性則值最小者,成本面屬性值最大者。
- ↑ 1.0 1.1 1.2 鄭哲男,劉立頌,黃冠翔. 多屬性決策方法應用於多重代理人協商.2005
- ↑ 2.0 2.1 2.2 Evangelos Triantaphyllou, B. Shu, Salvador Nieto Sanchez, and Tony Ray, Multi-Criteria Decision Making: An Operations Research Approach, Encyclopedia of Electrical and Electronics Engineering,(J. G. Webster, Ed.),John Wiley & Sons, New York, NY, 1998
- ↑ Lahdelma Risto, Salminen Pekka and Hokkanen Joonas, “Using multicriteria methods in environmental planning and management,” Environmental Management, Vol. 26, No.6, pp595-605, 2000
- ↑ Dyer James S., Sarin Rakesh K., “Measurable Multiattribute Value Functions,”Operations Research,Vol.27, No.4, pp.810-822,1979
- ↑ K. Paul Yoon and Hwang, Ching-Lai Hwang, Multiple Attribute Decision Making:An Introduction, Sage Publications Inc.,Thousand Oaks,1995







