最優化原理
出自 MBA智库百科(https://wiki.mbalib.com/)
最優化原理(Principle of optimality)
目錄 |
最優化原理是指要求目前存在的多種可能的方案中,選出最合理的,達到事先規定的最優目標的方案,這類問題稱之為最優化問題。其中,在所有可能的方案中,選出最合理的,達到事先規定的最優目標的方案稱之為最優方案。即一個最優策略的子策略,對於它的初態和終態而言也必是最優的。
最優化原理可以幫助解決生產實踐、工程設計、經濟管理等領域中涉及的最優計劃、最優分配、最優決策、最佳管理等最優化問題,培養應用最優化方法解決實際問題的能力。
1951年美國數學家R.Bellman等人,根據一類多階段問題的特點,把多階段問題變換為一系列互相聯繫的單階段問題,然後逐個加以解決。一些靜態模型,只要人為地引進“時間”因素,分成時段,就可以轉化成多階段的動態模型,用動態規劃方法去處理。與此同時,他提出瞭解決這類問題的“最優化原理”(Principle of optimality):
“一個過程的最優決策具有這樣的性質:即無論其初始狀態和初始決策如何,其今後諸策略對以第一個決策所形成的狀態作為初始狀態的過程而言,必須構成最優策略”。簡言之,一個最優策略的子策略對於它的初態和終態而言也必是最優的。
這個“最優化原理”如果用數學化一點的語言來,描述的話,就是:假設為瞭解決某一優化問題,需要依次作出n個決策D1,D2,…,Dn,如若這個決策序列是最優的,對於任何一個整數K,1<K<n,不論前面K個決策是怎樣的,以後的最優決策只取決於由前面決策所確定的當前狀態,及以後的決策Dk + 1,Dk + 2,…,Dn也是最優的。
最優化原理是動態規劃的基礎。任何一個問題,如果失去了這個最優化原理的支持,就不可能用動態規劃方法計算。能採用動態規劃求解的問題都需要滿足一定的條件:
1、問題中的狀態必須滿足最優化原理。
2、問題中的狀態必須滿足無後效性。
所謂的無後效性是指:“下一時刻的狀態只與當前狀態有關,而和當前狀態之前的狀態無關,當前的狀態是對以往決策的總結”。
動態規劃所處理的問題是一個多階段決策問題,一般由初始狀態開始,通過對中間階段決策的選擇,達到結束狀態。這些決策形成了一個決策序列,同時確定了完成整個過程的一條活動路線(通常是求最優的活動路線)。如圖所示。動態規劃的設計都有著一定的模式,一般要經歷以下幾個步驟。
初始狀態→|決策1|→|決策2|→|決策3|→…→|決策n|→結束狀態
1、劃分階段:按照問題的時間或空間特征,把問題分為若幹個階段。在劃分階段時,註意劃分後的階段一定要是有序的或者是可排序的,否則問題就無法求解。
2、確定狀態和狀態變數:將問題發展到各個階段時所處於的各種客觀情況用不同的狀態表示出來。當然,狀態的選擇要滿足無後效性。
3、確定決策並寫出狀態轉移方程:因為決策和狀態轉移有著天然的聯繫,狀態轉移就是根據上一階段的狀態和決策來導出本階段的狀態。所以如果確定了決策,狀態轉移方程也就可寫出。但事實上常常是反過來做,根據相鄰兩段各狀態之間的關係來確定決策。
4、尋找邊界條件:給出的狀態轉移方程是一個遞推式,需要一個遞推的終止條件或邊界條件。
動態規劃的主要難點在於理論上的設計,也就是上面4個步驟的確定,一旦設計完成,實現部分就會非常簡單。使用動態規劃求解問題,最重要的就是確定動態規劃三要素:問題的階段,每個階段的狀態以及從前一個階段轉化到後一個階段之間的遞推關係。
遞推關係必須是從次小的問題開始到較大的問題之間的轉化,從這個角度來說,動態規劃往往可以用遞歸程式來實現,不過因為遞推可以充分利用前面保存的子問題的解來減少重覆計算,所以對於大規模問題來說,有遞歸不可比擬的優勢,這也是動態規划算法的核心之處。
確定了動態規劃的這三要素,整個求解過程就可以用一個最優決策表來描述,最優決策表示一個二維表,其中行表示決策的階段,列表示問題狀態,表格需要填寫的數據一般對應此問題的在某個階段某個狀態下的最優值(如最短路徑,最長公共子序列,最大價值等),填表的過程就是根據遞推關係,從1行1列開始,以行或者列優先的順序,依次填寫表格,最後根據整個表格的數據通過簡單的取捨或者運算求得問題的最優解。下麵分別以求解最大化投資回報問題和最長公共子序列問題為例闡述用動態規划算法求解問題的一般思路。
原理的具體應用[1]
設某股份公司籌集到資金800萬元,該公司有4個項目需進行投資。根 據對各個項目的分析預測,得到各項目的投資額與年獲利潤的相關資料如下表:
| X(百萬元) | g1(X)(萬元) | g2(X)(萬元) | g3(X)(萬元) | g4(X)(萬元) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 30 | 40 | 40 | 50 |
| 2 | 60 | 50 | 90 | 90 |
| 3 | 80 | 70 | 130 | 150 |
| 4 | 100 | 90 | 180 | 180 |
| 5 | 110 | 100 | 190 | 200 |
| 6 | 110 | 210 | 210 | |
| 7 | 140 | 130 | 220 | 230 |
| 8 | 150 | 140 | 230 | 240 |
第一階段。這時第一個項目是唯一的 顯然有:f(n) = g1(X)(X=0,1,2,3,⋯⋯ 8) 其結果可列表如下:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| f1(X) | 0 | 30 | 60 | 80 | 100 | 110 | 120 | 140 | 150 |
| 最優策略 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
第二階段:研究在兩個項目之間進行投資的最優分配,使得獲利為最大。 其公式為:f2(8)=max{g1(Z)+f1(8 − Z)},Z=0,1,⋯⋯,8
f2(8)=max =max
=max =190,最優策略為(4,4),
=190,最優策略為(4,4),
即對第二個項目的投資均為400萬元,這時利潤總額為190萬元。
當這兩個項目的投資額為700萬元時,所創造的最大利潤為:
f2(7)=max{g2(Z)+f1(8 − Z)},Z=0,1,⋯⋯,8
f2(7)=max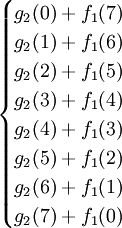 =max
=max =170,最優策略為(4,3)或(3,4),
=170,最優策略為(4,3)或(3,4),
f2(6)=max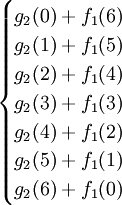 =max
=max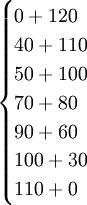 =150,最優策略為(5,1)或(4,2)或(3,3)或(2,4),
=150,最優策略為(5,1)或(4,2)或(3,3)或(2,4),
f2(5)=max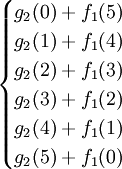 =max
=max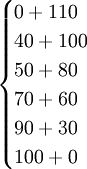 =140,最優策略為(4,1),
=140,最優策略為(4,1),
f2(4)=max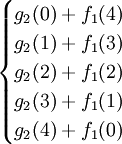 =max
=max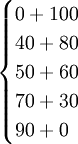 =120,最優策略為(3,1),
=120,最優策略為(3,1),
f2(3)=max =max
=max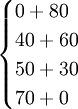 =100,最優策略為(2,1),
=100,最優策略為(2,1),
f2(2)=max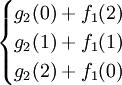 =max
=max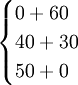 =70,最優策略為(1,1),
=70,最優策略為(1,1),
f2(1)=max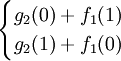 =max
=max =40,最優策略為(0,1),
=40,最優策略為(0,1),
以上第二階段的計算結果可列表如上:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| f2(X) | 0 | 40 | 70 | 100 | 120 | 140 | 150 | 170 | 190 |
| 最優策略 | 0 | (0,1) | (1,1) | (2,1) | (3,1) | (4,1) | (4,2) | (4,3) | (4,4) |
最優化理論與演算法在資訊理論中應用,使用最優化課程中解決非線性目標函數、線性約束函數極值問題的可行方向法中的Zoutendijk方法,結合Matlab軟體中的數值,計算工具箱對資訊理論中的問題進行編程分析和求解。最優化原理方法的引入,能夠從數值計算的角度給出相關定理的解釋,有助於加深對資訊理論中香農定理的理解。
最優化原理的方法主要研究對象是各種有組織系統的管理問題及其生產經營活動。最優化方法的目的在於針對所研究的系統,求得一個合理運用人力、物力和財力的最佳方案,發揮和提高系統的效能及效益,最終達到系統的最優目標。
- ↑ 張葉峰.動態規劃法在投資分配決策中的應用.中國科技博覽[J],2011,(35):318







