最优化原理
出自 MBA智库百科(https://wiki.mbalib.com/)
最优化原理(Principle of optimality)
目录 |
最优化原理是指要求目前存在的多种可能的方案中,选出最合理的,达到事先规定的最优目标的方案,这类问题称之为最优化问题。其中,在所有可能的方案中,选出最合理的,达到事先规定的最优目标的方案称之为最优方案。即一个最优策略的子策略,对于它的初态和终态而言也必是最优的。
最优化原理可以帮助解决生产实践、工程设计、经济管理等领域中涉及的最优计划、最优分配、最优决策、最佳管理等最优化问题,培养应用最优化方法解决实际问题的能力。
1951年美国数学家R.Bellman等人,根据一类多阶段问题的特点,把多阶段问题变换为一系列互相联系的单阶段问题,然后逐个加以解决。一些静态模型,只要人为地引进“时间”因素,分成时段,就可以转化成多阶段的动态模型,用动态规划方法去处理。与此同时,他提出了解决这类问题的“最优化原理”(Principle of optimality):
“一个过程的最优决策具有这样的性质:即无论其初始状态和初始决策如何,其今后诸策略对以第一个决策所形成的状态作为初始状态的过程而言,必须构成最优策略”。简言之,一个最优策略的子策略对于它的初态和终态而言也必是最优的。
这个“最优化原理”如果用数学化一点的语言来,描述的话,就是:假设为了解决某一优化问题,需要依次作出n个决策D1,D2,…,Dn,如若这个决策序列是最优的,对于任何一个整数K,1<K<n,不论前面K个决策是怎样的,以后的最优决策只取决于由前面决策所确定的当前状态,及以后的决策Dk + 1,Dk + 2,…,Dn也是最优的。
最优化原理是动态规划的基础。任何一个问题,如果失去了这个最优化原理的支持,就不可能用动态规划方法计算。能采用动态规划求解的问题都需要满足一定的条件:
1、问题中的状态必须满足最优化原理。
2、问题中的状态必须满足无后效性。
所谓的无后效性是指:“下一时刻的状态只与当前状态有关,而和当前状态之前的状态无关,当前的状态是对以往决策的总结”。
动态规划所处理的问题是一个多阶段决策问题,一般由初始状态开始,通过对中间阶段决策的选择,达到结束状态。这些决策形成了一个决策序列,同时确定了完成整个过程的一条活动路线(通常是求最优的活动路线)。如图所示。动态规划的设计都有着一定的模式,一般要经历以下几个步骤。
初始状态→|决策1|→|决策2|→|决策3|→…→|决策n|→结束状态
1、划分阶段:按照问题的时间或空间特征,把问题分为若干个阶段。在划分阶段时,注意划分后的阶段一定要是有序的或者是可排序的,否则问题就无法求解。
2、确定状态和状态变量:将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然,状态的选择要满足无后效性。
3、确定决策并写出状态转移方程:因为决策和状态转移有着天然的联系,状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策,状态转移方程也就可写出。但事实上常常是反过来做,根据相邻两段各状态之间的关系来确定决策。
4、寻找边界条件:给出的状态转移方程是一个递推式,需要一个递推的终止条件或边界条件。
动态规划的主要难点在于理论上的设计,也就是上面4个步骤的确定,一旦设计完成,实现部分就会非常简单。使用动态规划求解问题,最重要的就是确定动态规划三要素:问题的阶段,每个阶段的状态以及从前一个阶段转化到后一个阶段之间的递推关系。
递推关系必须是从次小的问题开始到较大的问题之间的转化,从这个角度来说,动态规划往往可以用递归程序来实现,不过因为递推可以充分利用前面保存的子问题的解来减少重复计算,所以对于大规模问题来说,有递归不可比拟的优势,这也是动态规划算法的核心之处。
确定了动态规划的这三要素,整个求解过程就可以用一个最优决策表来描述,最优决策表示一个二维表,其中行表示决策的阶段,列表示问题状态,表格需要填写的数据一般对应此问题的在某个阶段某个状态下的最优值(如最短路径,最长公共子序列,最大价值等),填表的过程就是根据递推关系,从1行1列开始,以行或者列优先的顺序,依次填写表格,最后根据整个表格的数据通过简单的取舍或者运算求得问题的最优解。下面分别以求解最大化投资回报问题和最长公共子序列问题为例阐述用动态规划算法求解问题的一般思路。
原理的具体应用[1]
设某股份公司筹集到资金800万元,该公司有4个项目需进行投资。根 据对各个项目的分析预测,得到各项目的投资额与年获利润的相关资料如下表:
| X(百万元) | g1(X)(万元) | g2(X)(万元) | g3(X)(万元) | g4(X)(万元) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 30 | 40 | 40 | 50 |
| 2 | 60 | 50 | 90 | 90 |
| 3 | 80 | 70 | 130 | 150 |
| 4 | 100 | 90 | 180 | 180 |
| 5 | 110 | 100 | 190 | 200 |
| 6 | 110 | 210 | 210 | |
| 7 | 140 | 130 | 220 | 230 |
| 8 | 150 | 140 | 230 | 240 |
第一阶段。这时第一个项目是唯一的 显然有:f(n) = g1(X)(X=0,1,2,3,⋯⋯ 8) 其结果可列表如下:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| f1(X) | 0 | 30 | 60 | 80 | 100 | 110 | 120 | 140 | 150 |
| 最优策略 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
第二阶段:研究在两个项目之间进行投资的最优分配,使得获利为最大。 其公式为:f2(8)=max{g1(Z)+f1(8 − Z)},Z=0,1,⋯⋯,8
f2(8)=max =max
=max =190,最优策略为(4,4),
=190,最优策略为(4,4),
即对第二个项目的投资均为400万元,这时利润总额为190万元。
当这两个项目的投资额为700万元时,所创造的最大利润为:
f2(7)=max{g2(Z)+f1(8 − Z)},Z=0,1,⋯⋯,8
f2(7)=max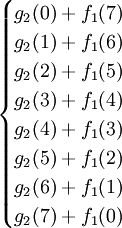 =max
=max =170,最优策略为(4,3)或(3,4),
=170,最优策略为(4,3)或(3,4),
f2(6)=max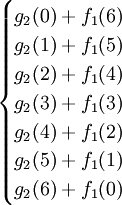 =max
=max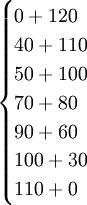 =150,最优策略为(5,1)或(4,2)或(3,3)或(2,4),
=150,最优策略为(5,1)或(4,2)或(3,3)或(2,4),
f2(5)=max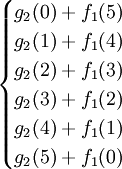 =max
=max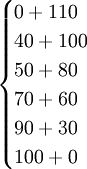 =140,最优策略为(4,1),
=140,最优策略为(4,1),
f2(4)=max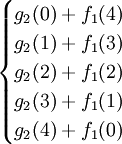 =max
=max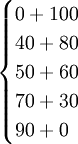 =120,最优策略为(3,1),
=120,最优策略为(3,1),
f2(3)=max =max
=max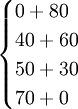 =100,最优策略为(2,1),
=100,最优策略为(2,1),
f2(2)=max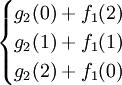 =max
=max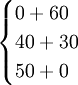 =70,最优策略为(1,1),
=70,最优策略为(1,1),
f2(1)=max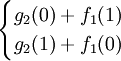 =max
=max =40,最优策略为(0,1),
=40,最优策略为(0,1),
以上第二阶段的计算结果可列表如上:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| f2(X) | 0 | 40 | 70 | 100 | 120 | 140 | 150 | 170 | 190 |
| 最优策略 | 0 | (0,1) | (1,1) | (2,1) | (3,1) | (4,1) | (4,2) | (4,3) | (4,4) |
最优化理论与算法在信息论中应用,使用最优化课程中解决非线性目标函数、线性约束函数极值问题的可行方向法中的Zoutendijk方法,结合Matlab软件中的数值,计算工具箱对信息论中的问题进行编程分析和求解。最优化原理方法的引入,能够从数值计算的角度给出相关定理的解释,有助于加深对信息论中香农定理的理解。
最优化原理的方法主要研究对象是各种有组织系统的管理问题及其生产经营活动。最优化方法的目的在于针对所研究的系统,求得一个合理运用人力、物力和财力的最佳方案,发挥和提高系统的效能及效益,最终达到系统的最优目标。
- ↑ 张叶峰.动态规划法在投资分配决策中的应用.中国科技博览[J],2011,(35):318







