工程分析法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　工程分析法又叫技術定額法，主要是根據企業的設備參數、工藝參數、標準的技術費用等工程技術指標，來確定不同產量水平下企業的平均成本。通過比較不同產量時的平均成本曲線，以確定企業的適度規模。

　　優點是比較準確，具有操作簡便，能夠根據工藝或工廠系統的技術能力，較真實地反映技術的規模經濟性本質。

　　主要缺點是要求分析者熟悉工程技術，且計算比較複雜。且僅考慮了生產的工程技術因素，而忽視了市場需求。此外，設定條件如產品結構、費用定額的確定可因專家經歷背景相異、使用標準不很統一而不同。

　　因此，工程分析法一般只適宜於分析那些市場結構穩定、需求波動不大的企業適度規模。

　　1.工程分析法原理

　　工程分析法是基於形象描述實際工程破壞問題而簡化的解析分析方法。用工程分析法計算盾構施工過程中，管片襯砌與周圍岩土體之間150mm縫隙引起的樁體應力和位移變化。

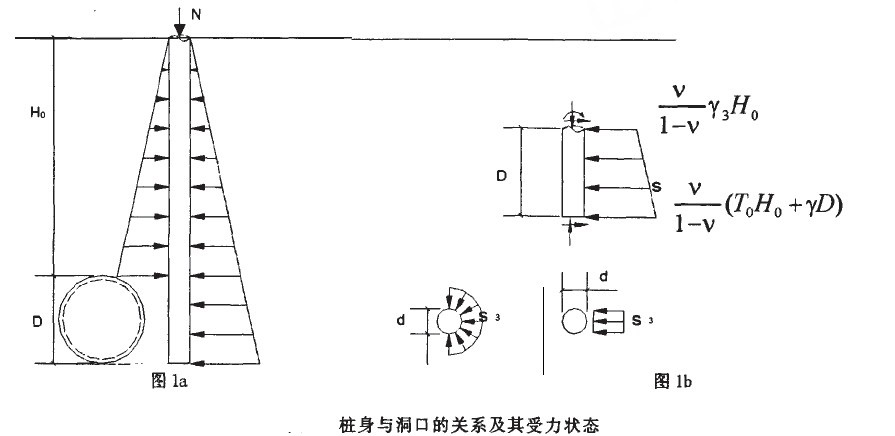
　　盾構向前推進時，需在盾構機的後部對已安裝好1．5m長的圓環砼管片進行註漿，此時，圓環管片與周圍的岩土體存在15cm的間隙。當隧道在樁側穿過時，由於間隙的存在，在隧道的一側，作用於樁的土壓力接近零，而樁的另一側，土壓力仍然存在，因而有壓力差，在這種壓力差的作用下，樁將產生水平位移、彎曲甚至強度破壞。因此，要分析計算寬度1．5m兩截面處土的摩擦力能否平衡土壓力，若不平衡，樁將產生彎曲，成為壓彎構件(圖la)，圖1b中表示樁側面土壓力的大小。

　　雖然近隧道一側不存在土壓力，但約有d/4範圍內的岩體將抵抗壓力差，即由圖1b可知：

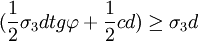
　　(1)

　　當研究隧道頂面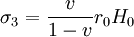，(2)

　　式中：γ₀為H₀深度範圍內岩土層的平均重度，H₀為地面至樁底的長度，C、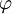、v分別為地基土的內聚力和內摩擦角。

　　由(1)和(2)得：

　　(3)

　　當H₀不滿足以上條件時，便會產生樁的彎曲，此時作用於樁的荷載q(kN/m)為：

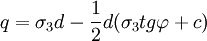　　(4)

　　在該荷載q的作用下，樁將產生彎曲，根據樁底與隧道位置的關係，彎矩為：

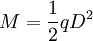
　　偏心距　(5)

　　隧道在強風化泥質砂岩中c=100kPa,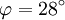,v=0.3,

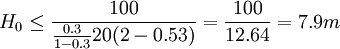
　　2.工程分析法應用

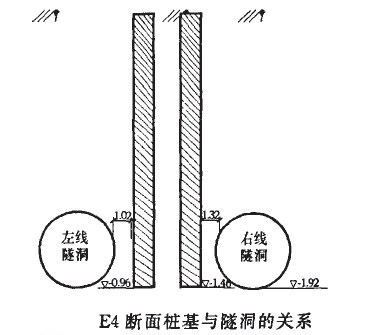
　　(1)對客村立交橋E4樁(上圖所示)，H₀ = 10.5m，c=100kPa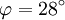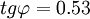，，，v=0.3，γ = 20kN/m³則由式(1)算得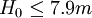，現H₀為10.5m，會產生樁的彎曲，必須計算q，由式(2)及(4)得：

　　σ₃ = 90kPa,q=37kPa

　　按懸臂梁考慮，

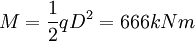　　樁配筋為20Φ25,由該彎矩計算所得該梁樁底的最大正應力為σ_max = 2MPa。

　　樁身水平位移：

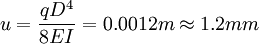
　　考慮到該樁不是懸臂梁，估計位移應增大1.5—1.7倍，即達到1.8～2.0mm。

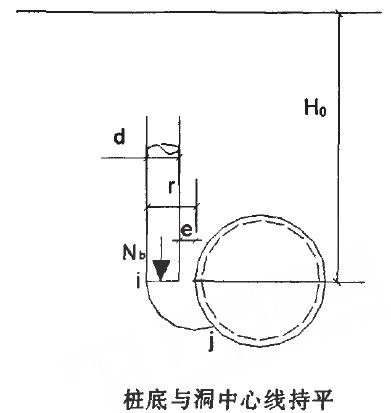
　　對於樁底與洞中心線持平的情況(上圖所示)，樁的沉降可假定高度為r的無側嚮應力σ₃的柱體壓縮減去已有岩體的壓縮S_r加上由於側嚮應力σ₃消失而引起樁的沉降，即：

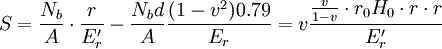　　(6)

　　式中：N_b為樁底載荷，r為假定剪切麵的半徑 為考慮無σ₃時的E_r，可取：

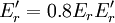
　　(2)對客村立交橋W5樁，N_b = 1821kN,d=1.5m,

　　A = 1.77m²,r=2.3m,v=0.2,γ₀ = 20kN / m³,

　　H₀ = 13.5m,E_r = 400MPa = 400000kPa,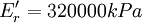

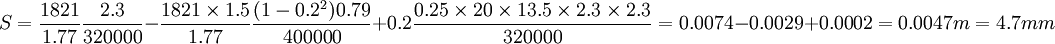
　　這表明，客村立交橋W5樁的沉降為4.7mm。

• 適者生存法