多元概率比回歸模型
用手机看条目
出自 MBA智库百科(https://wiki.mbalib.com/)
(重定向自多元概率比(Probit)回归模型)
目錄 |
[編輯]
多元概率比回歸模型亦稱Probit回歸模型,是假定企業破產的概率為p,並假設企業樣本服從標準正態分佈,其概率函數的p分位元數可以用財務指標線性解釋。
[編輯]
先是確定企業樣本的極大似然函數,通過求似然函數的極大值得到參數a、b,然後利用公式如下,求出企業破產的概率。和前面的判別規則一樣,如果概率p小於0.5,就判別為財務正常型;如果p大於0.5,則為即將破產型。
P = 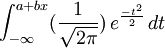
[編輯]
採用多元概率比回歸模型的前提條件[1]
企業樣本服從標準正態分佈,概率函數p分位數可以用財務指標線性解釋。
[編輯]
Probit模型和Logit模型的思路很相似,但在具體的計算方法和假設前提上又有一定的差異,主要體現在三個方面:
- 一是假設前提不同,Logit不需要嚴格的假設條件,而 Probit則假設企業樣本服從標準正態分佈,其概率函數的p分位元數可以用財務指標線性解釋;
- 二是參數a、b的求解方法不同,Logit採用線性回歸方法求解,而Probit採用極大似然函數求極值的方法求解;
- 三是求破產概率的方法不同,Logit採用取對數方法,而Probit採用積分的方法。
[編輯]
假設條件比較嚴格,計算過程複雜,且有較多近似處理,但預測精確度高。
[編輯]
[編輯]
- ↑ 程濤.財務預警模型綜述[J].山西財經大學學報,2003,25(5):105








胡扯,純粹地瞎說