哈恩－巴拿赫定理
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
在泛函分析中，哈恩-巴拿赫定理是一個極為重要的工具。它允許了定義在某個向量空間上的有界線性運算元擴張到整個空間，並說明瞭存在“足夠”的連續函數。定義在每一個賦範向量空間，使對偶空間的研究變得有趣味。這個定理以漢斯•哈恩和斯特凡•巴拿赫命名，他們在1920年獨立證明瞭這個定理。
定理的最一般的表述需要一些準備。給定標量域（實數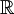
或複數
）上的一個向量空間V，一個函數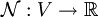
稱為次線性函數，如果：
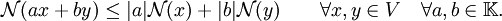
可以很容易證明，V上的每一個範數和每一個半範數都是次線性的。其它的次線性函數也可以是很有用的。
哈恩-巴拿赫定理說明，如果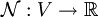是一個次線性函數，
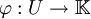是V的線性子空間|子空間U上的一個線性泛函，滿足：
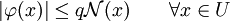
那麼存在φ到整個空間V的一個線性擴張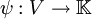
，也就是說，存在一個線性泛函ψ，使得：
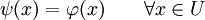
以及：
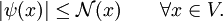
擴張ψ一般不是由φ唯一指定的，定理的證明也沒有給出任何求出ψ的方法：在無窮維空間V的情形中，它依賴於佐恩引理——選擇公理的一個表述。
我們可以把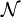
的次線性條件稍微減弱，只需要：
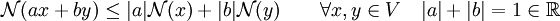
這揭示了哈恩-巴拿赫定理與凸性的密切聯繫。
這個定理有一些重要的結果，其中有些也有時稱為“哈恩-巴拿赫定理”：
如果V是一個賦zh-tw:范向量空間，其子空間為U（不一定是封閉的），且φ : U → K是連續和線性的，那麼存在φ的一個擴張ψ : V → K，也是連續和線性的，且範數與φ相同（關於線性映射的範數的討論，參見巴拿赫空間）。也就是說，在賦zh-tw:范向量空間的範疇中，空間K是一個內射對象。
如果V是一個賦zh-tw:范向量空間，其子空間為U（不一定是封閉的），且z是V的一個元素，不在U的閉包 (拓撲學)|閉包內，那麼存在一個連續線性映射ψ : V → K，對於U內的所有x都滿足ψ(x) = 0，ψ(z) = 1，且||ψ|| = 1/dist(z,U)。
哈恩-巴拿赫定理的另外一種形式，稱為哈恩-巴拿赫分離定理。它在凸幾何中有許多用途。
定理：設V為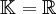 
或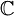
上的一個拓撲向量空間，A和B 是 V的非空凸子集。假設
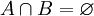。那麼：
如果A是開集，那麼存在一個連續線性映射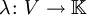
和 
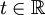，使得對於所有的
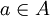和
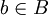，都有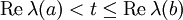 
。
如果V 是局部凸的，A 是緊集，且B 是閉集，那麼存在一個連續線性映射 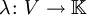和 
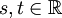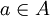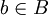，使得對於所有的和，都有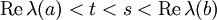 
。
前面已經提到，從選擇公理可以推出哈恩-巴拿赫定理。然而，反過來不成立。註意超濾子引理比選擇公理更弱，但從它也可以推出哈恩-巴拿赫定理（反過來則不行）。實際上，哈恩-巴拿赫定理還可以用比超濾子引理更弱的假設來證明。[1]對於可分空間|可分巴拿赫空間，Brown和Simpson證明瞭哈恩-巴拿赫定理可以從WKL0——一個二階算術的弱子系統推出。[2]
- ↑ D. Pincus, The strength of Hahn–Banach's Theorem, in: Victoria Symposium on Non-standard Analysis, Lecture notes in Math. 369, Springer 1974, pp. 203-248. Citation from M. Foreman and F. Wehrung,
- ↑ D. K. Brown and S. G. Simpson, Which set existence axioms are needed to prove the separable Hahn-Banach theorem?, Annals of Pure and Applied Logic, 31, 1986, pp. 123-144.
