分組分析法

出自 MBA智库百科(https://wiki.mbalib.com/)

　　分組分析法是指通過統計分組的計算和分析，來認識所要分析對象的不同特征，不同性質及相互關係的方法。

　　分組就是根據研究的目的和客觀現象的內在特點，按某個標誌或幾個標誌把被研究的總體劃分為若幹個不同性質的組，使組內的差異儘可能小，組間的差異儘可能大。分組分析法是在分組的基礎上，對現象的內部結構或現象之問的依存關係從定性或定量的角度做進一一步分析研究，以便尋找事物發展的規律，正確的分析問題和解決問題。

　　分組時必須遵循兩個原則：窮盡原則和互斥原則。所謂窮盡原則，就是使總體中的每一個單位都應有組可歸，或者說各分組的空間足以容納總體所有的單位。所謂互斥原則，就是在特定的分組標誌下，總體中的任何一個單位只能歸屬與某一個組，而不能同時或可能歸屬與幾個組。

根據分組分析法作用的不同，分為結構分組分析法和相關關係分組分析法。結構分組分析法又可分為按品質標誌分組和按數量標誌分組。

　　1．結構分組分析法

　　(1)按品質標誌分組分析法

　　分組是確定社會經濟現象同質總體，研究現象各種類型的基礎。俗話說“物以類聚，人以群分”，在複雜的社會經濟現象總體中，客觀上存在著多種多樣的類型，各種不同的類型有著不同的特點以及不同的發展規律，而且同類事物聚集在一起，結合為同一類別或群體。分組可以將複雜的社會經濟現象，按照量化研究的要求區分為一個個性質不同的類型，以進一步研究各組的數量特征和組與組之間的相互關係。按照不同的類別分辨事物，就不會混淆事物的性質，就可以認識萬物的本質特征。

　　廣義上說，任何統計分組都是把現象總體劃分為不同的類型；

　　狹義上說，劃分現象類型是指對某一複雜總體按重要的品質標誌來分組，以反映不同性質的社會經濟現象之間的相互關係。科學分組是區分現象的類型、正確瞭解、研究現象的實質，發揮統計研究作用的重要工具。

　　品質標誌分組分析法就是用來分析社會經濟現象的各種類型特征，從而找出客觀事物規律的一種分析方法。

　　(2)按數量標誌分組分析法

　　數量標誌分組分析法是用來研究總體內部結構及其變化的一種分析方法。

總體現象在科學分組的基礎上，計算各組單位數或分組指標量在總體總量中所占比重，形成了總體的結構分佈狀況。各組所占比重數大小不同，說明它們在總體中所處的地位不同，對總體分佈特征的影響也不同，其中比重數相對大的部分，決定著總體的性質或結構類型。藉助於總體各部分的比重在量上的差異和聯繫，用以研究總體內部各部分之間存在的差異和相互聯繫。

　　(3)相關關係分組分析法

　　相關關係分組分析法是用來分析社會經濟現象之間依存關係的一種分組分析法。

　　社會經濟現象之間存在著廣泛的聯繫和制約關係，其中關係緊密地一種聯繫就是現象之間的依存關係。如商品流轉額中商品流轉速度與流通費用率之間存在著依存關係；工業產品的單位成本、銷售總額與利潤也呈依存關係。分析研究現象之間依存關係的統計方法很多，如相關回歸分析法、指數因素分析法、分組分析法等，其中統計分組分析法是最基本的方法，是進行其它分析的基礎。

　　分組分析法分析現象之間的依存關係，是將現象之間屬於影響因素原因標誌作為自變數，而把屬於被影響因素的結果指標作為崗變數。首先對總體按原因標誌分組，其次按組計算出被影響因素的平均指標或相對指標，然後根據指標值在各組間的變動規律來確定自變數與因變數之間的依存關係，認識現象之間在數量上的影響作用和程度。

　　綜上所述，分組分析法是以按品質標誌分組分析法為前提條件，通過品質標誌分組分析法，可以分析現象的類型特征和規律性；利用按數量標誌分組分析法分析現象總體內部的結構及其變化；利用相關_關係分組分析法可以分析社會經濟現象之間的相關關係。這三種分組分析法在實際中常常結合在一起使用。

　　(一)選擇分組標誌

　　要進行科學分組，必須選擇適當的分組標誌。分組標誌就是作為分組依據的標準。統計分組的關鍵在於選擇分組標誌和劃分各組界限，選擇分組標誌是統計分組的核心問題，因為分組標誌與分組的目的有直接關係。任何一個統計總體都可以採用許多分組標誌分組。分組時採用的分組標誌不同，其分組的結果及由此得出的結論也會不同。這是因為分組標誌一經選定必然表現出總體在這個標誌上的差異情況，但同時又掩蓋了其他標誌的差異。如果分組標誌選擇不恰當，不但 無法表現出總體的基本特征，甚至會把不同質的事物混在一起，從而掩蓋和歪曲現象的本質特征。劃分各組界限，就是要在分組標誌的變異範圍內劃定各相鄰組間的性質界限和數量界限。那麼如何正確選擇分組標誌呢?

　　第一，要根據統計研究的目的選擇分組標誌；

　　第二，必鬚根據事物內部矛盾的分析選擇反映事物本質的分組標誌；

　　第三，結合被研究事物所處的具體歷史條件選擇分組標誌。

　　(二)確定組距和組數

　　按照數量標誌分組時，在確定了分組標誌之後，就應根據被研究的現象總體的數量特征，採用適當的分組形式，確定相宜的組距和組數。

　　組數的確定一般與數據本身的特點及數據的多少有關，由於分組的目的之一是為了觀察數據分佈的特征，因此組數的多少應適中，如組數太少，數據的分佈就會過於集中，組數太多，數據的分佈就會過於分散，這都不便於觀察數據分佈的特征和規律。組數的確定應以能夠顯示數據的分佈特征和規律為目的。在實際分組時，我們可以按斯特奇斯(Sturges)給出的經驗公式來確定組數K：

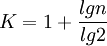
　　式中，挖為數據的個數，對結果用四捨五入的辦法取整數即為組數。當然，這是一個經驗公式，實際應用中，可根據數據的多少和特點及分析的要求，參考這一表準靈活確定組數。

　　組距(class width)是一個組的上限與下限的差，可根據全部數據的最大值和最小值及所分的組數來確定，即組距=(最大值一最小值)／組數。為便於計算，組距宜取5或10的倍數，而且第一組的下限應底於最小變數值，最後一組的上限應高於最大變數值，因此組距可取10。

　　(三)計算組中值併進行分析

　　確定了數據的組距和組數後，我們就可以藉助一些統計變數來對數據進行分析了。為了反映各組數據的一般水平，我們通常用組中值(class midpoint)作為該組數據的一個代表值，即組中值一(下限值+上限值)／2，但這種代表有一個必要的假定條件，即各組數據在本組內呈均勻分佈或在組中值兩側呈對稱分佈，如實際數據的分佈不符合這一假定，用組中值作為一組數據的代表值會有一定的誤差。