伯特蘭-切比雪夫定理
出自 MBA智库百科(https://wiki.mbalib.com/)
伯特蘭-切比雪夫定理(Bertrand Chebyshev theorem)
目錄 |
伯特蘭-切比雪夫定理是指1845年約瑟•伯特蘭提出的猜想。伯特蘭檢查了2至3×106之間的所有數。1850年切比雪夫證明瞭這個猜想。拉馬努金給出較簡單的證明,而保羅•艾狄胥則借二項式繫數給出了另一個簡單的證明。
伯特蘭-切比雪夫定理說明:若整數n > 3,則至少存在一個質數p,符合n < p < 2n − 2。另一個稍弱說法是:對於所有大於1的整數n,存在一個質數p,符合n < p < 2n。
詹姆斯•約瑟夫•西爾維斯特證明:k個大於k的連續整數之積,是一個大於k的質數的倍數。
艾狄胥證明:對於任意正整數k,存在正整數N使得對於所有n > N,n和2n之間有k個質數。
他又證明k = 2、N = 6時,而且有,其中兩個質數分別是4的倍數加1,4的倍數減1。
根據質數定理,n和2n之間的質數數目是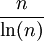 。
。
證明的方法是運用反證法,反設定理不成立,然後用兩種方法估計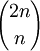 的上下界,得出矛盾的不等式
的上下界,得出矛盾的不等式
註:下麵的證明中,都假設p屬於質數集。
這條不等式是關於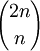 的下界的。
的下界的。
對於正整數n,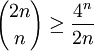
證明 :
對於 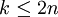 ,
, 
若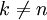 ,
,
因此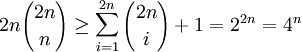
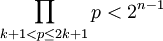
證明:
註意到所有大於 k+1 而小於 2k+1 的質數都在(2k+1)! 中而不在(k+1)! 或 k! 中,於是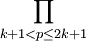 是
是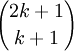 的因數。
的因數。

同時又有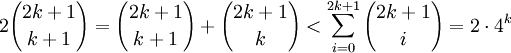
於是就有 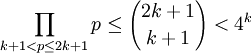
這個定理和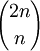 的上界有關。
的上界有關。
對於所有正整數n, 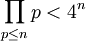
當n = 2,2 < 16,成立。
假設對於所有少於n的整數,敘述都成立。
顯然,若n>2且n是偶數,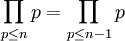 。對於奇數的n,設n=2k+1。
。對於奇數的n,設n=2k+1。
從引理1和歸納假設可得:
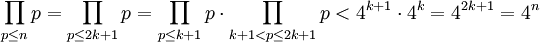
首先的定理:
若p是質數,n是整數。設s是最大的整數使得ps | n! ,則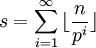
下麵這些系理和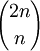 的上界有關。
的上界有關。
若p為質數,設sp是最大的整數使得 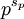 整除
整除 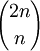 ,則:
,則:
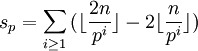
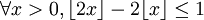 ,所以
,所以
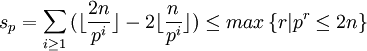
於是得到三個上界:
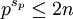
若 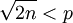 ,
, 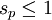
若 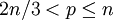 ,sp = 0(因為 2n! 中只有兩個 p,在 n! 中恰有一個 p)
,sp = 0(因為 2n! 中只有兩個 p,在 n! 中恰有一個 p)
假設存在大於1的正整數n,使得沒有質數p符合n < p < 2n。根據系理1.2和1.3:
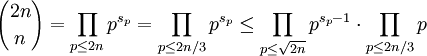
再根據系理1.1和定理1:
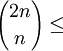 上式最右方
上式最右方 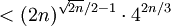
結合之前關於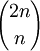 的下界的不等式1:
的下界的不等式1:
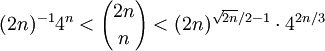
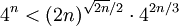
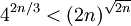
兩邊取2的對數,並設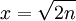 :
:
xln2 − 3lnx < 0。
顯然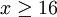 ,即
,即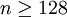 時,此式不成立,得出矛盾。
時,此式不成立,得出矛盾。
因此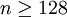 時,伯特蘭—切比雪夫定理成立。
時,伯特蘭—切比雪夫定理成立。
再在n < 128時驗證這個假設即可。







