伯特兰-切比雪夫定理
出自 MBA智库百科(https://wiki.mbalib.com/)
伯特兰-切比雪夫定理(Bertrand Chebyshev theorem)
目录 |
伯特兰-切比雪夫定理是指1845年约瑟•伯特兰提出的猜想。伯特兰检查了2至3×106之间的所有数。1850年切比雪夫证明了这个猜想。拉马努金给出较简单的证明,而保罗•艾狄胥则借二项式系数给出了另一个简单的证明。
伯特兰-切比雪夫定理说明:若整数n > 3,则至少存在一个质数p,符合n < p < 2n − 2。另一个稍弱说法是:对于所有大于1的整数n,存在一个质数p,符合n < p < 2n。
詹姆斯•约瑟夫•西尔维斯特证明:k个大于k的连续整数之积,是一个大于k的质数的倍数。
艾狄胥证明:对于任意正整数k,存在正整数N使得对于所有n > N,n和2n之间有k个质数。
他又证明k = 2、N = 6时,而且有,其中两个质数分别是4的倍数加1,4的倍数减1。
根据质数定理,n和2n之间的质数数目是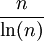 。
。
证明的方法是运用反证法,反设定理不成立,然后用两种方法估计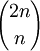 的上下界,得出矛盾的不等式
的上下界,得出矛盾的不等式
注:下面的证明中,都假设p属于质数集。
这条不等式是关于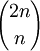 的下界的。
的下界的。
对于正整数n,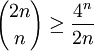
证明 :
对于 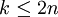 ,
, 
若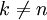 ,
,
因此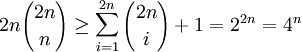
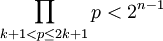
证明:
注意到所有大于 k+1 而小于 2k+1 的质数都在(2k+1)! 中而不在(k+1)! 或 k! 中,于是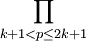 是
是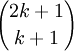 的因子。
的因子。

同时又有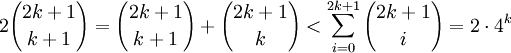
于是就有 
这个定理和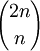 的上界有关。
的上界有关。
对于所有正整数n, 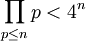
当n = 2,2 < 16,成立。
假设对于所有少于n的整数,叙述都成立。
显然,若n>2且n是偶数,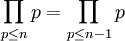 。对于奇数的n,设n=2k+1。
。对于奇数的n,设n=2k+1。
从引理1和归纳假设可得:
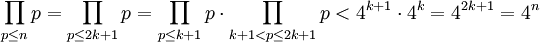
首先的定理:
若p是质数,n是整数。设s是最大的整数使得ps | n! ,则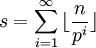
下面这些系理和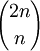 的上界有关。
的上界有关。
若p为质数,设sp是最大的整数使得 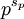 整除
整除 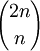 ,则:
,则:
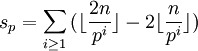
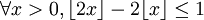 ,所以
,所以
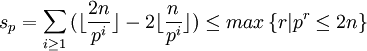
于是得到三个上界:
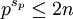
若 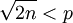 ,
, 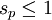
若 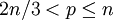 ,sp = 0(因为 2n! 中只有两个 p,在 n! 中恰有一个 p)
,sp = 0(因为 2n! 中只有两个 p,在 n! 中恰有一个 p)
假设存在大于1的正整数n,使得没有质数p符合n < p < 2n。根据系理1.2和1.3:
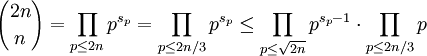
再根据系理1.1和定理1:
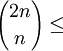 上式最右方
上式最右方 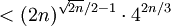
结合之前关于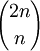 的下界的不等式1:
的下界的不等式1:
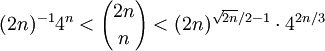
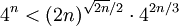
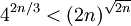
两边取2的对数,并设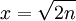 :
:
xln2 − 3lnx < 0。
显然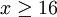 ,即
,即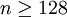 时,此式不成立,得出矛盾。
时,此式不成立,得出矛盾。
因此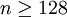 时,伯特兰—切比雪夫定理成立。
时,伯特兰—切比雪夫定理成立。
再在n < 128时验证这个假设即可。







