全球专业中文经管百科，由121,994位网友共同编写而成，共计436,015个条目

查看

工具箱▼

生长曲线(S曲线)预测法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

(重定向自Growth curve models)

生长曲线(S曲线)预测法(Growth curve)

目录

1 什么是生长曲线(S曲线)预测法
2 生长曲线预测模型[1]
3 相关条目
4 参考文献

什么是生长曲线(S曲线)预测法

　　生长曲线预测法也称生长曲线模型（Growth curve models）是预测事件的一组观测数据随时间的变化符合生长曲线的规律，以生长曲线模型进行预测的方法。一般来说，事物总是经过发生、发展、成熟三个阶段，而每一个阶段的发展速度各不相同。通常在发生阶段，变化速度较为缓慢；在发展阶段，变化速度加快；在成熟阶段，变化速度又趋缓慢，按上述三个阶段发展规律得到的变化曲线称为生长曲线。

生长曲线预测模型^[1]

皮尔模型

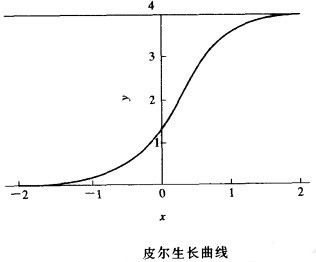
　　皮尔生长曲线的一般模型为

　　 $\frac x{K}{1+e^{f(x)}}$

　　式中，K为常数(如某种耐用消费品饱和状态时的普及率)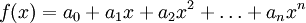； $f(x)=a_0+a_1x+a_2x^2+\ldots+a_nx^n$ 。

　　常用的皮尔生长曲线模型为

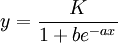　　 $y=\frac{K}{1+be^{-ax}}$ (2)　　a>0,b>0

　　这时f(x)是x的线性函数，且具有负斜率。见下图是皮尔曲线模型的图。

林德诺模型

　　常用于新技术发展和新产品销售的一种预测方法。

龚帕兹模型

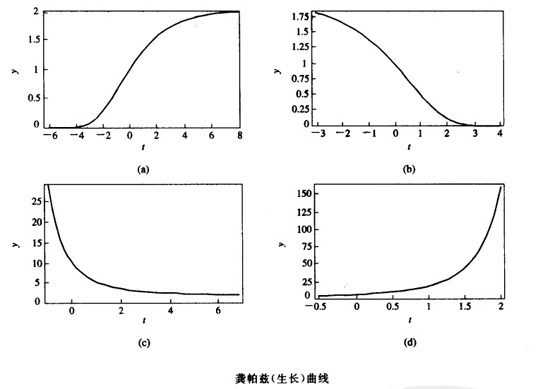
　　龚帕兹(生长)曲线是一种常用曲线，其形式为

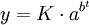　　 $y=K\cdot a^{b^t}$ K＞0，a＜1，0＜b＜1　　(11)

　　对参数a、b、K的不同取值，龚帕兹模型有不同的形状和变化趋势。图(a)为1n a＜0，0＜b＜l时的龚帕兹曲线；图(b)为1n a＜0，b＞1时的曲线；图(c)为1n a＞0，0＜b＜1时的曲线；图(d)为ln a＞0，b＞1时的曲线。

　　给定时间序列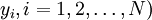 $y_i,i=1,2,\ldots,N)$ ,只要求得其中的三个参数值a、b、K，就可以用来求得未来周期的预测值。

　　求参数a、b、K的方法有多种，如非线性回归分析、特殊函数的最小二乘法等。这里介绍一种比较简单的方法，其步骤如下：

　　(1)将N个数据分成三组(这里假设N=3r)；

　　(2)求各组的 $y i$ 值的对数和，即求：

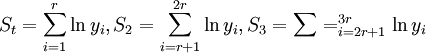
　　 $S_t=\sum_{i=1}^r\ln y_i,S_2=\sum_{i=r+1}^{2r}\ln y_i,S_3=\sum=_{i=2r+1}^{3r}\ln y_i$

　　(3)利用下列公式计算参数a、b、K的值；

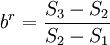　　 $b^r=\frac{S_3-S_2}{S_2-S_1}$ (12)

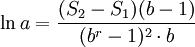　　 $\ln a=\frac{(S_2-S_1)(b-1)}{(b^r-1)^2\cdot b}$ (13)

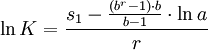　　 $\ln K=\frac{s_1-\frac{(b^r-1)\cdot b}{b-1}\cdot \ln a}{r}$ (14)

　　(4)直接计算K值的公式为

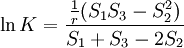　　 $\ln K=\frac{\frac{1}{r}(S_1S_3-S_2^2)}{S_1+S_3-2S_2}$ (15)

相关条目

参考文献

↑ 李华,胡奇英.预测与决策[M].ISBN:7-5606-1495-7/G303;C934.西安电子科技大学出版社.2005(05)

来自"https://wiki.mbalib.com/wiki/%E7%94%9F%E9%95%BF%E6%9B%B2%E7%BA%BF%28S%E6%9B%B2%E7%BA%BF%29%E9%A2%84%E6%B5%8B%E6%B3%95"

打开MBA智库App, 阅读完整内容打开App

如果您认为本条目还有待完善，需要补充新内容或修改错误内容，请编辑条目或投诉举报。

本条目由以下用户参与贡献

页面分类: 统计方法

评论(共0条)

提示:评论内容为网友针对条目"生长曲线(S曲线)预测法"展开的讨论，与本站观点立场无关。

发表评论请文明上网，理性发言并遵守有关规定。

以上内容根据网友推荐自动排序生成

闽公网安备 35020302032707号