需求的价格点弹性
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
当需求曲线上两点之间的变化量趋于无穷小时,需求的价格弹性要用点弹性来表示。也就是说,需求的价格点弹性表示需求曲线上某一点上的需求量变动对于价格变动的反应程度。需求的价格点弹性的公式为:

可见,需求的价格弧弹性和点弹性本质是相同的,它们的区别仅在于:前者表示价格变动量较大时的需求曲线上两点之间的弹性,而后者表示价格变动量无穷小时的需求曲线上某一点的弹性。
例如某商品需求函数为Qd = 2400 − 400P,求a点(P=5,Q=400)和b点(P=4,Q=800)的需求的价格点弹性。根据公式可以计算出a、b两点的需求的价格弹性如下:
由需求函数Qd = 2400 − 400P可得点弹性的计算公式为: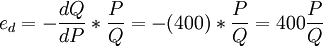
所以,a点的需求的价格点弹性系数为: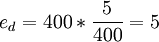 ;
;
b点的需求的价格点弹性系数为: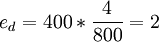 ;
;
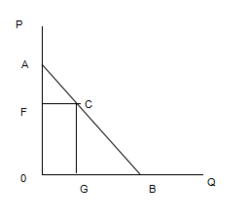
首先分析线性的需求曲线上的点弹性。如图1所示,线性需求曲线为QD = f(P),它与纵坐标和横坐标分别相效于A、B两点,令C点为该线性需求曲线上的任意一点。
根据点弹性的定义,需求曲线上C点的需求的价格点弹性可以表示为:
从公式中可以得到三种计算和判断线性需求曲线上点弹性的方法:
斜线公式: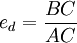 ,其含义是,当C点位于线性需求曲线AB的中点时,点弹性等于1;当C点位于线性需求曲线AB的中点以上时,点弹性大于1;当C点位于线性需求曲线AB的中点以下时,点弹性小于1。
,其含义是,当C点位于线性需求曲线AB的中点时,点弹性等于1;当C点位于线性需求曲线AB的中点以上时,点弹性大于1;当C点位于线性需求曲线AB的中点以下时,点弹性小于1。
横轴公式: ,即以横轴线段GB和OG表示点弹性大小。点G越靠近原点,则C点的点弹性越大,反之,越小。若G点为OB的中点,则C点的点弹性为1。
,即以横轴线段GB和OG表示点弹性大小。点G越靠近原点,则C点的点弹性越大,反之,越小。若G点为OB的中点,则C点的点弹性为1。
纵轴公式: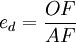 ,即以纵轴曲线段OF和AF表示点弹性大小。点F越靠近原点,则C点的点弹性越小,反之,则越大。若F恰为OA的中点,则C点的弹性为1。
,即以纵轴曲线段OF和AF表示点弹性大小。点F越靠近原点,则C点的点弹性越小,反之,则越大。若F恰为OA的中点,则C点的弹性为1。
从上述点弹性的几何意义上可以看出,对于任意一条线性需求曲线上的点来说,它在需求曲线上的位置越高,相应的点弹性数值就越大;相反,位置越低,相应的点弹性系数值越小。这一特征可用图3—4表示如下:
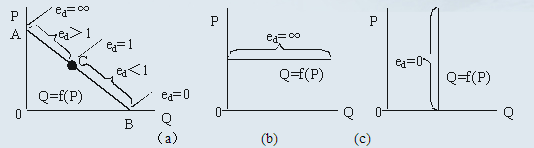
从图2(a)中可以看出,对于一般的线性需求曲线来说,曲线上的每一点的需求的价格点弹性是不相等的。在线性需求曲线与横轴的交点B,点弹性为0,在线性需求曲线与纵轴的交点A,点弹性为∞。对于特殊的线性需求曲线来说,水平的需求曲线(b图)上每一点的点弹性均为无穷大,即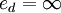 ;垂直的需求曲线(c图)上每一点的点弹性均为零,即ed = 0。
;垂直的需求曲线(c图)上每一点的点弹性均为零,即ed = 0。
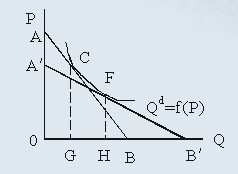
再来分析非线性需求曲线的点弹性。用3来说明。
在C点有: 。在F点有:
。在F点有: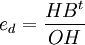 。
。
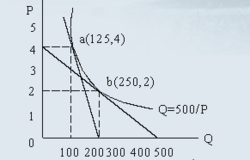
在非线性需求曲线中,直角双曲线上的点弹性的特点是,每点的点弹性都是1。设直角双曲线为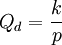 (其中k为大于零的常数),不管价格变化率是多少,需求量总以相同的比率成反方向变化。在图4中,需求函数
(其中k为大于零的常数),不管价格变化率是多少,需求量总以相同的比率成反方向变化。在图4中,需求函数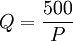 的几何图形是一条直角双曲线,曲线上每一点的点弹性都是单位弹性ed = 1,例如,在a点:
的几何图形是一条直角双曲线,曲线上每一点的点弹性都是单位弹性ed = 1,例如,在a点: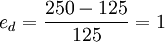 ;
;
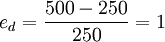 ,如此等等。
,如此等等。
需求直角双曲线的点弹性具有这一特点的原因在于:对于任何的需求直接双曲线函数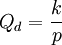 来说,不管价格的变化率为多少,需求量总是以相同的比率成反方向的变化,从而使得需求曲线上每点的点弹性系数的值均为1。
来说,不管价格的变化率为多少,需求量总是以相同的比率成反方向的变化,从而使得需求曲线上每点的点弹性系数的值均为1。
最后,要注意需求曲线的斜率和需求的价格弹性是两个不同的概念。从点弹性的计算公式-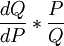 中可以看出,需求线上某一点的斜率为
中可以看出,需求线上某一点的斜率为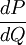 ,而该点的点弹性不仅取决于该点斜率的倒数
,而该点的点弹性不仅取决于该点斜率的倒数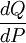 ,还取决于相应的价格——需求量的比值
,还取决于相应的价格——需求量的比值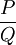 。也就是说,线性需求曲线上任一点的斜率都是相等的,而每一点的点弹性不相同的。
。也就是说,线性需求曲线上任一点的斜率都是相等的,而每一点的点弹性不相同的。








几何意义与种类中,请问点弹性的-dq/dp为什么=GB/CG呢