法图引理

出自 MBA智库百科(https://wiki.mbalib.com/)

法图引理(Fatou lemma)

　　在测度论中，法图引理是指一个函数列的下极限的勒贝格积分和其积分的下极限的不等关系。法图引理的名称来源于法国数学家皮埃尔•法图（Pierre Fatou），被用来证明测度论中的法图-勒贝格定理和勒贝格控制收敛定理。

　　设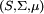为一个测度空间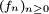， 是一个实值的可测正值函数列。那么：

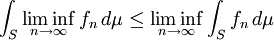
　　其中的函数极限是在逐点收敛的意义上的极限，函数的取值和积分可以是无穷大。

　　定理的证明基于单调收敛定理（非常容易证明）。设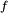为函数列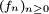 的下极限。对每个正整数 k ，逐点定义下极限函数：

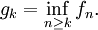
　　于是函数列g₁, g₂, . . .单调递增并趋于 。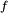

　　任意k ≤ n，我们有g_k ≤ f_n，因此

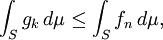
　　于是

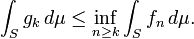
　　据此，由单调收敛定理以及下极限的定义，就有：

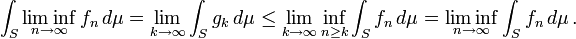
　　令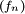为测度空间(S,Σ,μ)中的一列可测函数，函数的值域为扩展的实数轴。如果存在一个在 S 上可积的正值函数 g ，使得对所有的 n 都有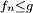，那么

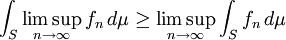
　　这里只需弱可积，即。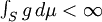

　　证明：对函数列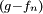应用法图引理即可。

　　法图引理不仅对取正值的函数列成立，在一定限制条件下，可以扩展到任意的实值函数。令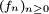为测度空间(S,Σ,μ)中的一列可测函数，函数的值域为扩展的实数轴。如果存在一个在 S 上可积的正值函数 g ，使得对所有的 n 都有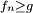，那么

　　证明：对函数列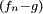应用法图引理即可。

　　在以上的条件下，如果函数列在S上μ-几乎处处逐点收敛到一个函数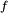，那么

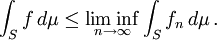
　　证明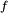：是函数列的极限，因此自然是下极限。此外，零测集上的差异对于积分值没有影响。

　　如果函数列在S上依测度收敛到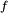，那么上面的命题仍然成立。

　　证明：存在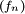的一个子列使得

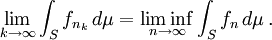
　　这个子列仍然依测度收敛到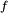，于是又存在这个子列的一个子列在S 上μ-几乎处处逐点收敛到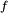，于是命题成立。