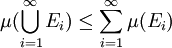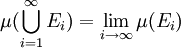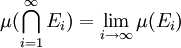测度
出自 MBA智库百科(https://wiki.mbalib.com/)
测度(Measure)
目录 |
数学上,测度(Measure)是一个函数,它对一个给定集合的某些子集指定一个数,这个数可以比作大小、体积、概率等等。传统的积分是在区间上进行的,后来人们希望把积分推广到任意的集合上,就发展出测度的概念,它在数学分析和概率论有重要的地位。
测度论是实分析的一个分支,研究对象有σ代数、测度、可测函数和积分,其重要性在概率论和统计学中有所体现的。
形式上说,一个测度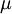 (详细的说法是可列可加的正测度)是个函数。设
(详细的说法是可列可加的正测度)是个函数。设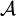 是集合
是集合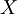 上的一个σ代数,
上的一个σ代数,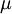 在上
在上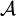 定义,于扩充区间
定义,于扩充区间![[0,\infty]](/w/images/math/3/1/5/315e0047ccbfa87354192dac2fe986fb.png) 中取值,并且满足以下性质:
中取值,并且满足以下性质:
- 空集的测度为零:
-
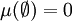 。
。
-
- 可数可加性,或称σ可加性:若
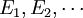 为
为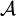 中可数个两两不交的集合的序列,则所有
中可数个两两不交的集合的序列,则所有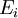 的并集的测度,等于每个
的并集的测度,等于每个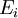 的测度之总和:
的测度之总和:
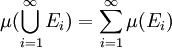 。
。
这样的三元组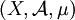 称为一个测度空间,而
称为一个测度空间,而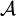 中的元素称为这个空间中的可测集。
中的元素称为这个空间中的可测集。
下面的一些性质可从测度的定义导出:
测度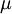 的单调性:
的单调性:
若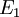 和
和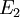 为可测集,而且
为可测集,而且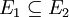 ,则
,则 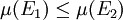 。
。
若 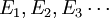 为可测集(不必是两两不交的),并且对于所有的
为可测集(不必是两两不交的),并且对于所有的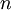 ,
, ⊆
⊆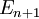 ,则集合
,则集合 的并集是可测的,且有如下不等式(「次可列可加性」):
的并集是可测的,且有如下不等式(「次可列可加性」):
以及如下极限:
若 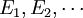 为可测集,并且对于所有的
为可测集,并且对于所有的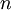 ,
,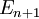 ⊆
⊆ ,则
,则 的交集是可测的。进一步说,如果至少一个
的交集是可测的。进一步说,如果至少一个 的测度有限,则有极限:
的测度有限,则有极限:
如若不假设至少一个 的测度有限,则上述性质一般不成立。例如对于每一个
的测度有限,则上述性质一般不成立。例如对于每一个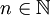 ,令
,令
这里,全部集合都具有无限测度,但它们的交集是空集。
如果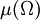 是一个有限实数(而不是
是一个有限实数(而不是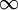 ),则测度空间
),则测度空间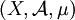 称为有限测度空间。如果
称为有限测度空间。如果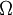 可以表示为可数个可测集的并集,而且这些可测集的测度均有限,则该测度空间称为σ有限测度空间。称测度空间中的一个集合
可以表示为可数个可测集的并集,而且这些可测集的测度均有限,则该测度空间称为σ有限测度空间。称测度空间中的一个集合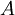 具有σ有限测度,如果
具有σ有限测度,如果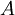 可以表示为可数个可测集的并集,而且这些可测集的测度均有限。
可以表示为可数个可测集的并集,而且这些可测集的测度均有限。
作为例子,实数集赋以标准勒贝格测度是σ有限的,但不是有限的。为说明之,只要考虑闭区间族[k, k+1],k 取遍所有的整数;这样的区间共有可数多个,每一个的测度为1,而且并起来就是整个实数集。作为另一个例子,取实数集上的计数测度,即对实数集的每个有限子集,都把元素个数作为它的测度,至于无限子集的测度则令为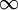 。这样的测度空间就不是σ有限的,因为任何有限测度集只含有有限个点,从而,覆盖整个实数轴需要不可数个有限测度集。σ有限的测度空间有些很好的性质;从这点上说,σ有限性可以类比于拓扑空间的可分性。
。这样的测度空间就不是σ有限的,因为任何有限测度集只含有有限个点,从而,覆盖整个实数轴需要不可数个有限测度集。σ有限的测度空间有些很好的性质;从这点上说,σ有限性可以类比于拓扑空间的可分性。
一个可测集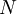 称为零测集,如果
称为零测集,如果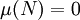 。零测集的子集称为可去集,它未必是可测的,但零测集自然是可去集。如果所有的可去集都可测,则称该测度为完备测度。
。零测集的子集称为可去集,它未必是可测的,但零测集自然是可去集。如果所有的可去集都可测,则称该测度为完备测度。
一个测度可以按如下的方式延拓为完备测度:考虑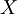 的所有这样的子集
的所有这样的子集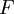 ,它与某个可测集
,它与某个可测集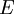 仅差一个可去集,也就是说
仅差一个可去集,也就是说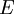 与
与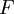 的对称差包含于一个零测集中。由这些子集
的对称差包含于一个零测集中。由这些子集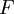 生成的σ代数,并定义
生成的σ代数,并定义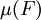 的值就等于
的值就等于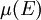 。
。
下列是一些测度的例子(重要性与顺序无关)。
- 计数测度 定义为
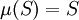 的‘元素个数’。
的‘元素个数’。
- 一维勒贝格测度 是定义在
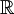 的一个含所有区间的σ代数上的、完备的、平移不变的、满足
的一个含所有区间的σ代数上的、完备的、平移不变的、满足![\mu([0,1])=1\](/w/images/math/c/7/a/c7a36793073e1288383b0d6b7690dea7.png) 的唯一测度。
的唯一测度。
- Circular angle 测度 是旋转不变的。
- 局部紧拓扑群上的哈尔测度是勒贝格测度的一种推广,而且也有类似的刻划。
- 恆零测度 定义为
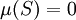 ,对任意的
,对任意的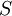 。
。
- 每一个概率空间都有一个测度,它对全空间取值为1(于是其值全部落到单位区间[0,1]中)。这就是所谓概率测度。
- 其它例子,包括:狄拉克测度、波莱尔测度、若尔当测度、遍历测度、欧拉测度、高斯测度、贝尔测度、拉东测度。